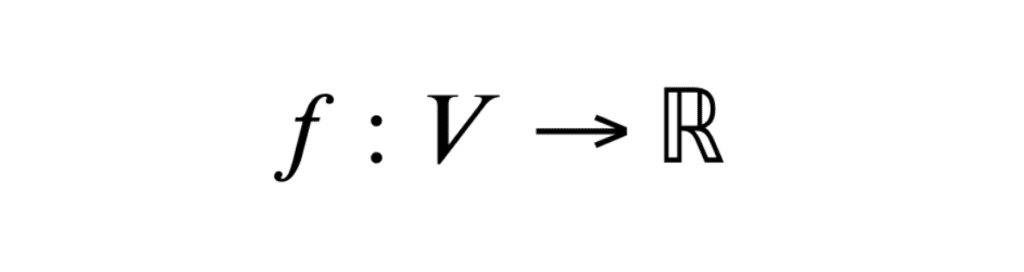Les formes linéaires constituent un concept fondamental dans l’étude de l’algèbre linéaire. Dans cet article, nous allons explorer la théorie des formes linéaires, étudier leurs propriétés et leur importance dans différents contextes. Les formes linéaires jouent un rôle essentiel dans l’analyse économique et la recherche opérationnelle. En effet, elles permettent de modéliser des problèmes d’optimisation, de prendre en compte des contraintes dans des modèles linéaires et d’analyser des fonctions de coût ou de profit. Aujourd’hui, nous étudierons plusieurs notions hors programme sur ces applications. Cela te permettra de te préparer aux épreuves parisiennes, notamment aux Maths I et aux oraux de mathématiques.
Qu’est-ce qu’une forme linéaire ?
Une forme linéaire est une application linéaire d’un espace vectoriel dans son corps de base. En ECG, nous travaillerons uniquement sur \(\mathbb{R}\).
Formellement, si \(V\) est un espace vectoriel sur \( \mathbb{R}\), une forme linéaire est une fonction \(f: V \rightarrow \mathbb{R}\) qui respecte les deux conditions suivantes pour tous vecteurs \(u, v \in V\) et tout scalaire \(\alpha \in \mathbb{R}\) :
1. Additivité : \(f(u + v) = f(u) + f(v)\)
2. Homogénéité : \(f(\alpha u) = \alpha f(u)\)
Exemples de formes linéaires
Un exemple classique
Pour illustrer, considérons l’espace vectoriel \(V = \mathbb{R}^2\), et soit \(f\) une forme linéaire définie par \(f(x, y) = 3x – 2y\).
Cette fonction est linéaire, car elle respecte les deux conditions d’additivité et d’homogénéité mentionnées précédemment. De plus, cette application se fait bien entre un espace vectoriel et \(\mathbb{R}.\)
La trace d’une matrice
Un exemple notable d’une forme linéaire dans l’espace des matrices carrées \(M_n(\mathbb{R})\) est la trace. La trace d’une matrice \(A\), notée \(\text{Tr}(A)\), est la somme des éléments de sa diagonale principale. La trace est une forme linéaire, car \(\text{Tr}(A + B) = \text{Tr}(A) + \text{Tr}(B)\) et \(\text{Tr}(\lambda A) = \lambda \text{Tr}(A)\) pour toute matrice \(A, B \in M_n(\mathbb{R})\) et tout scalaire \(\lambda\).
De plus, cette application se fait bien entre un espace vectoriel, ici l’ensemble des matrices carrées \(M_n(\mathbb{R})\), et \(\mathbb{R}.\)
Représentation matricielle des formes linéaires
Toute forme linéaire peut être représentée par une matrice dans une base donnée. Si \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) est une forme linéaire et \(v\) est un vecteur de \(\mathbb{R}^n\), alors il existe une unique matrice ligne \(A\) telle que \(f(v) = Av\), où \(Av\) est le produit de la matrice \(A\) par le vecteur colonne \(v\).
Cette représentation matricielle simplifie l’analyse et le calcul des formes linéaires, notamment pour résoudre des systèmes d’équations linéaires ou optimiser des fonctions linéaires sous contraintes.
Lien avec le produit scalaire dans le cadre d’espaces euclidiens
Dans un espace euclidien, toute forme linéaire peut être représentée par le produit scalaire avec un vecteur fixe. Plus précisément, pour toute forme linéaire \(f\) sur un espace euclidien \(E\), il existe un vecteur unique \(u \in E\) tel que pour tout \(v \in E\), \(f(v) = \langle u, v \rangle\), où \(\langle \cdot, \cdot \rangle\) désigne le produit scalaire.
Cette représentation montre comment les formes linéaires peuvent être interprétées en termes de projections et de composantes dans des directions spécifiques.
Surjectivité d’une forme linéaire
La surjectivité est une propriété importante des fonctions en mathématiques, y compris des formes linéaires. Une forme linéaire \(f: V \rightarrow \mathbb{R}\) est dite surjective si pour tout élément \(k\) dans le corps de base \(\mathbb{R}\), il existe au moins un vecteur \(v\) dans \(V\) tel que \(f(v) = k\).
En termes simples, cela signifie que la forme linéaire peut atteindre n’importe quelle valeur dans le corps de base. Pour les formes linéaires, la surjectivité est toujours garantie dès lors que la forme linéaire n’est pas la fonction nulle, car les scalaires peuvent être ajustés pour atteindre n’importe quelle valeur cible dans \(\mathbb{R}\).
Lien entre le noyau d’une forme linéaire et un hyperplan
Le noyau d’une forme linéaire \(f: V \rightarrow \mathbb{R}\) sur un espace vectoriel \(V\) est l’ensemble des vecteurs qui sont envoyés sur zéro par \(f\). Une propriété fondamentale est que si \(f\) n’est pas la fonction nulle, alors son noyau définit un hyperplan dans \(V\).
Rappelons qu’un hyperplan est ici un sous-espace vectoriel de \(V\) de dimension \(\text{dim}(V) – 1\).
Démonstration
Soit \(f\) une forme linéaire non nulle sur \(V\), et soit \(v_0\) un vecteur dans \(V\) tel que \(f(v_0) = k \neq 0\). Le noyau de \(f\), noté \(\text{Ker}(f)\), est un sous-espace de \(V\). Pour tout vecteur \(v\) dans \(V\), le vecteur \(v – \frac{f(v)}{k}v_0\) est dans \(\text{Ker}(f)\) car \(f(v – \frac{f(v)}{k}v_0) = f(v) – \frac{f(v)}{k}f(v_0) = 0\).
Cela montre que chaque vecteur de \(V\) peut être écrit comme la somme d’un vecteur dans le noyau de \(f\) et d’un multiple scalaire de \(v_0\), impliquant que \(\text{Ker}(f)\) est un hyperplan.
Proportionnalité des formes linéaires avec le même noyau
Deux formes linéaires \(f\) et \(g\) sur un espace vectoriel \(V\) sont dites proportionnelles si l’une est un multiple scalaire de l’autre. C’est-à-dire \(f = \lambda g\) pour un certain scalaire \(\lambda\).
Une propriété intéressante est que si deux formes linéaires ont le même noyau (l’ensemble des vecteurs qui sont envoyés sur zéro), alors elles sont nécessairement proportionnelles.
Conclusion
Les formes linéaires sont un outil essentiel dans l’étude de l’algèbre linéaire et trouvent de multiples applications dans le domaine économique. Elles permettent de modéliser des situations variées, de simplifier l’analyse de problèmes complexes et de formuler des solutions optimales dans des contextes linéaires.
Maîtriser ce concept ouvre la porte à une meilleure compréhension des théories d’algèbre linéaire et à une application efficace des mathématiques dans les études économiques. En pratiquant régulièrement, par des exercices et des applications concrètes, tu renforceras ta compréhension et ta capacité à utiliser les formes linéaires dans divers exercices.
Pour t’entraîner sur cette notion, tu peux réaliser la dernière partie du sujet EML 2023 (mathématiques approfondies).
Tu peux retrouver ici toutes nos autres ressources mathématiques !