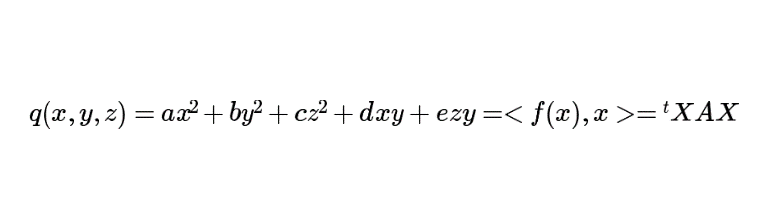L’objectif de cet article est de te donner toutes les clés pour réussir tous les exercices qui comportent des formes quadratiques. Cette notion est très récurrente et la maîtriser peut être utile pour réussir les épreuves de maths des Parisiennes comme les exercices de l’EDHEC ou de l’EMLyon. C’est une notion hors programme pour les maths appliquées, pour autant, cet article peut te servir, car tu pourras retrouver cette notion régulièrement dans les annales.
Soit \(n \in \mathbb{N}\)
Définition
Une forme quadratique est un polynôme de degré deux avec un nombre quelconque de variables réelles.
Par exemple, on pose \((a,b,c,d,e,x,y,z)\in \mathbb{R}^{8}\), alors \(q(x,y,z)=ax^2+by^2+cz^2+dxy+ezy\) est une forme quadratique.
Les différentes écritures
On peut écrire une forme quadratique de trois façons différentes en utilisant des outils mathématiques distincts.
L’écriture polynomiale
Il y a tout d’abord la forme polynomiale : \(\forall (x,y,z) \in \mathbb{R}^{3}, 2x^2+xy+3z^2+4zy\) est une forme quadratique.
L’écriture matricielle
Tu peux également utiliser les matrices pour écrire une forme quadratique.
On pose \(S\) une matrice symétrique de \(\mathbb{M}_{n}(R)\), soit \(X=\begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{pmatrix} \). Alors \({}^tXAX\) est une forme quadratique.
De manière générale, on pose \(A\) la matrice symétrique de terme général \((a_{i,j})\) avec \((i,j) \in \mathbb(N)\) et \( x=(x_{1},…x_{n})\) un vecteur de \(\mathbb{R}^n\). Alors \(q\) la forme quadratique associée à \(A\) est
\(q(x) = {}^tXAX = \displaystyle {\sum_{i=1}^{n}a_{i,i}x_{i}^{2} }+ 2 \displaystyle {\sum_{1 \le i < j \le n}} a_{i,j} x_{i}x_{j}\). On retrouve bien une forme polynomiale réelle de degré deux.
Donnons un exemple plus concret : si on pose \(A=\begin{pmatrix} \color{blue}{1} & \color{orange}{2} & 3 \\ \color{orange}{2} & \color{green}{4} & 1 \\ 3 & 1 & 0 \end{pmatrix}\) et \(X=\begin{pmatrix} x \\ y \\ z \end{pmatrix} \) alors \({}^tXAX=\color{blue}{1}x^2 +\color{green}{4}y^2+\color{orange}{4}xy+6xz+2yz\). On retrouve bien une forme polynomiale réelle de degré deux.
L’écriture avec les produits scalaires
Soit \(E\) un espace vectoriel de dimension finie, soit \(f\) un endomorphisme symétrique de \(E\), soit \(x\) un vecteur de \(E\) ; \(q(x)=<f(x),x>\) est également une forme quadratique.
En effet, si on pose \(A\) la matrice associée à \(f\) dans une base quelconque \(B\) de \(E\), alors \(A\) est symétrique et \(<f(x),x>={}^tXAX\). Donc, on a bien que \(<f(x),x>\) est une forme quadratique.
Résumé de ces trois écritures
Finalement, on peut résumer ces trois écritures en une nouvelle définition de la forme quadratique.
Soient \(E\) un espace vectoriel de dimension finie et \(F\) un sous-espace vectoriel de \(E\).
Une application \(q\) de \(E\) dans \(F\) est une forme quadratique sur \(E\) si, pour tout élément \(x\) de \(E\), \(q(x)\) est une expression polynomiale de degré deux par rapport aux coordonnées de \(x\) dans une base quelconque de \(E\).
Il est important pour toi de savoir reconnaître une forme quadratique lorsque tu rencontres ces trois écritures, cela te permettra d’appliquer d’office leurs propriétés et surtout, tu maîtriseras les outils mathématiques que tu utiliseras !
Tu retiendras que : \[\fbox{\(q(x,y,z)=ax^2+by^2+cz^2+dxy+ezy<f(x),x>={}^tXAX\)}\]
Propriétés
Soit \(q\) une forme quadratique d’un espace vectoriel \(E\), soit \(x\) un vecteur de \(E\) et \(\lambda\) un réel; \(q(\lambda x)=\lambda^2q(x)\).
Pour le démontrer, on utilise l’écriture avec les produits scalaires de la forme quadratique et les propriétés de linéarité de \(f\) et du produit scalaire ; \(q(\lambda x)=<f(\lambda x),\lambda x>=\lambda<\lambda f(x),x>=\lambda^2<f(x),x>=\lambda^2q(x)\).
Soit \(q\) une forme quadratique de \(E\), il existe une unique application bilinéaire \(\phi\) de \(E\) telle que \(\forall x \in E, q(x)=\phi(x,x)\).
Signe d’une forme quadratique
Afin de calculer le signe d’une forme quadratique, tu peux te référer à cet article qui caractérise les matrices symétriques positives. Tu y retrouveras certaines écritures qui te feront penser aux formes quadratiques !
En résumé, si les valeurs propres de \(A\) sont toutes strictement positives (ou strictement négatives), alors \(q\) est strictement positive (et respectivement strictement négative). On parle alors de forme quadratique définie positive.
Si \(q\) est une forme quadratique définie positive sur \(E\), alors \(\forall x \in, x \ne 0, q(x)>0\) et \(q(x)=0 \Leftrightarrow x=0\). On peut le démontrer par l’absurde : soit \(x \in E, x\ne 0 / q(x)=0\) on sait que \(\forall x \in E, x \ne 0, q(x)>0\) donc \(x=0\).
Exemple
Soit \(A=\begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & 2 \\ 1 & 2 & 3 \end{pmatrix}\). \(A\) est associé à la forme quadratique \(q\) telle que \(\forall (x,y,z) \in \mathbb(R)^3\), \(q(x,y,z)=x^2+2y^2+3z^2+2xy+2xz+4yz\). De plus, les valeurs propres de la matrice \(A\) sont toutes strictement positives (tu peux t’entraîner à les chercher). Ainsi, on en déduit que \(q\) est une forme quadratique définie positive.
Encadrement d’une forme quadratique
Soit \(A\) une matrice symétrique et \(q\) sa forme quadratique associée. Soit \(\lambda_m\) la plus petite valeur propre de \(A\) et \(\lambda_g\) la plus grande valeur propre de \(A\). Alors \(\forall u \in E, \lambda_m \|u\|^2 \le q(u) \le \lambda_g \|u\|^2 \).
Tu peux retrouver la démonstration de cet encadrement dans cet article.
ATTENTION ! Ces propriétés sont hors programme ECG, il est donc important de connaître les démonstrations et de toujours redémontrer le résultat si tu veux les utiliser. Cependant, les connaître peut t’aider à mieux comprendre les énoncés et à faire des liens entre les questions.
Lien entre forme quadratique et matrice hessienne
Une matrice hessienne est une matrice symétrique, donc elle est associée à une forme quadratique. Ainsi, connaître les propriétés des formes quadratiques peut être très utile dans le cadre de l’étude des hessiennes de fonctions à plusieurs variables afin de montrer qu’un point critique est un minimum ou un maximum.
Pour t’entraîner
En maths approfondies, tu peux approfondir cette notion grâce à l’exercice 2 d’Ecricome 2017 (sujet, corrigé) qui fait de l’optimisation sur une forme quadratique. Tu ne pourras le faire qu’après avoir vu le chapitre sur l’optimisation et les fonctions à plusieurs variables. L’épreuve de HEC 2015 (sujet, corrigé) cherche aussi le signe d’une forme quadratique.
N’hésite pas à consulter toutes nos ressources mathématiques.