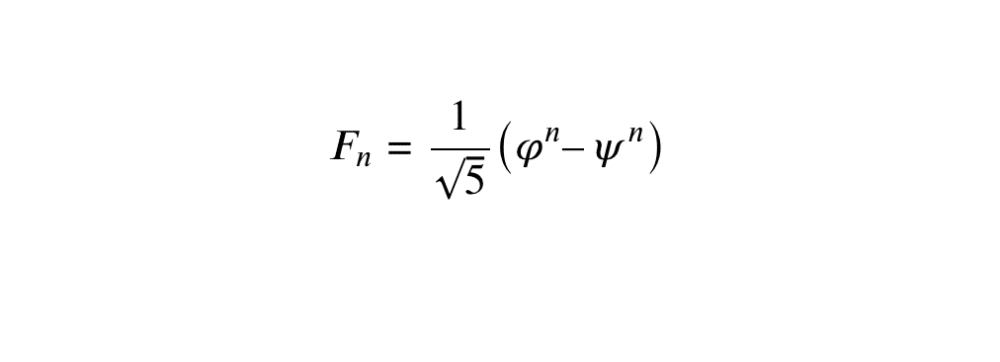La suite de Fibonacci, bien connue pour son apparition dans divers domaines des mathématiques et de la nature, est définie par une simple relation de récurrence. Cependant, derrière cette simplicité apparente se cache une formule remarquable qui permet de calculer directement n’importe quel terme de la suite sans avoir à passer par les termes précédents. Cette formule, connue sous le nom de formule de Binet, relie de manière élégante la suite de Fibonacci à des concepts plus larges comme le nombre d’or. Dans cet article, nous allons explorer en détail cette formule, en comprendre la démonstration et examiner ses nombreuses propriétés et applications.
Introduction à la formule de Binet
La suite de Fibonacci est l’une des suites les plus célèbres des mathématiques. Elle est définie de manière récurrente : chaque terme est la somme des deux termes qui le précèdent, avec les deux premiers termes fixés à 0 et 1. Formellement, on écrit :
\[ F_0 = 0, \quad F_1 = 1 \]
\[ F_n = F_{n-1} + F_{n-2}, \quad \text{pour } n \geq 2 \]
Bien que cette définition récurrente soit simple, elle ne donne pas directement une expression explicite pour le n-ième terme de la suite. C’est là qu’intervient la formule de Binet. Cette formule permet de calculer le n-ième terme de la suite de Fibonacci sans avoir à calculer tous les termes précédents.
La formule de Binet
La formule de Binet exprime le n-ième terme de la suite de Fibonacci comme suit :
\[
F_n = \frac{1}{\sqrt{5}} \left( \varphi^n – \psi^n \right)
\]
où :
\[
\varphi = \frac{1 + \sqrt{5}}{2} \quad \text{et} \quad \psi = \frac{1 – \sqrt{5}}{2}
\]
Ici, \(\varphi\) est le nombre d’or, bien connu en mathématiques, dans la nature et en art.
Interprétation de la formule
La formule de Binet peut paraître déroutante au premier abord, mais elle résume en réalité de manière élégante la croissance rapide des termes de la suite de Fibonacci. Le terme \(\varphi^n\) domine la croissance de \(F_n\) car \(\varphi > 1\), tandis que \(\psi^n\) devient rapidement négligeable au fur et à mesure que \(n\) augmente, car \(\psi\) est un nombre négatif dont la valeur absolue est inférieure à 1.
En conséquence, pour des valeurs de \(n\) grandes, \(F_n\) est approximativement égal à \( \displaystyle \frac{\varphi^n}{\sqrt{5}}\).
Formule de Binet et nombre d’or
La formule de Binet permet d’établir un lien mathématique direct entre la suite de Fibonacci et le nombre d’or, \( \displaystyle \varphi = \frac{1 + \sqrt{5}}{2}\). Pour démontrer que le rapport de deux termes consécutifs de la suite de Fibonacci tend vers \(\varphi\), considérons le rapport \( \frac{F_{n+1}}{F_n} \), en utilisant la formule de Binet :
\[
\frac{F_{n+1}}{F_n} = \frac{\frac{1}{\sqrt{5}} \left( \varphi^{n+1} – \psi^{n+1} \right)}{\frac{1}{\sqrt{5}} \left( \varphi^n – \psi^n \right)} = \frac{\varphi^{n+1} – \psi^{n+1}}{\varphi^n – \psi^n}
\]
En factorisant par \(\varphi^n\) au numérateur et au dénominateur, on obtient :
\[
\frac{F_{n+1}}{F_n} = \frac{\varphi \left(1 – \left(\frac{\psi}{\varphi}\right)^{n+1}\right)}{1 – \left(\frac{\psi}{\varphi}\right)^n}
\]
Comme \( \displaystyle \left|\frac{\psi}{\varphi}\right| < 1\), les termes \( \displaystyle \left(\frac{\psi}{\varphi}\right)^n\) et \( \displaystyle \left(\frac{\psi}{\varphi}\right)^{n+1}\) tendent vers 0 lorsque \(n\) augmente. Ainsi, lorsque \(n\) tend vers l’infini, le rapport \( \displaystyle \frac{F_{n+1}}{F_n}\) tend vers \(\varphi\), c’est-à-dire :
\[
\lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \varphi
\]
Cette démonstration montre que le nombre d’or n’est pas seulement une curiosité mathématique, mais une limite fondamentale dans la croissance des termes de la suite de Fibonacci, révélée par la formule de Binet.
Démonstration de la formule de Binet
Pour démontrer la formule de Binet, partons du fait que la suite de Fibonacci est une suite récurrente linéaire d’ordre 2, définie par la relation de récurrence :
\[
F_n = F_{n-1} + F_{n-2}
\]
La première étape consiste à associer à cette suite un polynôme caractéristique. Supposons que \(F_n = r^n\) soit une solution de cette relation. En substituant cette forme dans la récurrence, on obtient l’équation caractéristique suivante :
\[
r^n = r^{n-1} + r^{n-2}
\]
En divisant par \(r^{n-2},\) non nul de par la croissance de la suite, on obtient :
\[
r^2 – r – 1 = 0
\]
Il s’agit d’une équation quadratique dont les racines, notées \(\lambda_1\) et \(\lambda_2\), sont données par la formule quadratique :
\[
\lambda_{1,2} = \frac{1 \pm \sqrt{5}}{2}
\]
Ces racines, \( \displaystyle \lambda_1 = \varphi = \frac{1 + \sqrt{5}}{2}\) (le nombre d’or) et \( \displaystyle \lambda_2 = \psi = \frac{1 – \sqrt{5}}{2},\) sont réelles et distinctes puisque le discriminant \(\Delta = 1^2 + 4 \times 1 \times 1 = 5\) est strictement positif.
La solution générale de la suite récurrente est donc une combinaison linéaire des puissances de ces racines :
\[
F_n = a \lambda_1^n + b \lambda_2^n
\]
Les constantes \(a\) et \(b\) sont déterminées par les conditions initiales. Pour \(n = 0\) et \(n = 1\), on a :
\[
F_0 = a \lambda_1^0 + b \lambda_2^0 = a + b = 0
\]
\[
F_1 = a \lambda_1^1 + b \lambda_2^1 = a \lambda_1 + b \lambda_2 = 1
\]
De \(a + b = 0\), on en déduit que \(b = -a\). Substituons cette valeur dans la deuxième équation :
\[
a \lambda_1 – a \lambda_2 = 1
\]
\[
a (\lambda_1 – \lambda_2) = 1
\]
Sachant que \( \displaystyle \lambda_1 – \lambda_2 = \frac{1 + \sqrt{5}}{2} – \frac{1 – \sqrt{5}}{2} = \sqrt{5},\) on obtient :
\[
a = \frac{1}{\sqrt{5}}
\]
\[
b = -\frac{1}{\sqrt{5}}
\]
En substituant \(a\) et \(b\) dans la solution générale, on obtient la formule de Binet :
\[
F_n = \frac{1}{\sqrt{5}} \left( \varphi^n – \psi^n \right)
\]
Cette formule explicite permet de calculer directement n’importe quel terme de la suite de Fibonacci sans avoir besoin de recourir à la définition par récurrence.
Propriétés et applications de la formule de Binet
Propriétés asymptotiques
Comme mentionné précédemment, pour de grandes valeurs de \(n\), \(\psi^n\) devient très petit, et \(F_n\) peut être approximé par \( \displaystyle \frac{\varphi^n}{\sqrt{5}}\). Cette approximation montre que la suite de Fibonacci croît de manière exponentielle.
Utilisation dans la combinatoire
La formule de Binet n’est pas seulement un outil théorique, elle a des applications pratiques, notamment en combinatoire. Par exemple, les nombres de Fibonacci permettent de compter le nombre de façons de couvrir une bande \(1 \times n\) avec des dominos \(1 \times 2\). La formule de Binet permet de compter rapidement ces configurations pour des valeurs élevées de \(n\).
Racines de polynômes et suite de Fibonacci
La connexion entre les nombres de Fibonacci et les racines de polynômes est également une application intéressante. Par exemple, la racine positive de l’équation quadratique \(x^2 – x – 1 = 0\) est \(\varphi\), et cette racine est directement liée à la croissance des termes de la suite de Fibonacci.
Cela illustre comment la suite de Fibonacci apparaît naturellement dans des contextes liés aux racines de polynômes. Ainsi, la formule de Binet est directement liée aux nombres dont le carré est égal à eux-mêmes lorsqu’on leur rajoute 1, c’est-à-dire les racines du polynôme ci-dessus.
Conclusion
La formule de Binet offre une perspective profonde sur la suite de Fibonacci, reliant des concepts tels que le nombre d’or et les solutions d’équations quadratiques. Ainsi, elle est non seulement un outil puissant pour calculer des termes spécifiques de la suite, mais elle révèle aussi des propriétés asymptotiques et des connexions avec d’autres domaines des mathématiques. Comprendre cette formule enrichit notre appréciation de la beauté et de l’élégance des structures mathématiques.
Bien que la formule de Binet soit hors programme, la compréhension approfondie des propriétés liées à cette égalité te permettra d’améliorer tes compétences en analyse. Donc, l’étude de cette notion te préparera pour les épreuves écrites et orales de mathématiques.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés ! Tu peux également accéder à toutes nos autres ressources mathématiques !