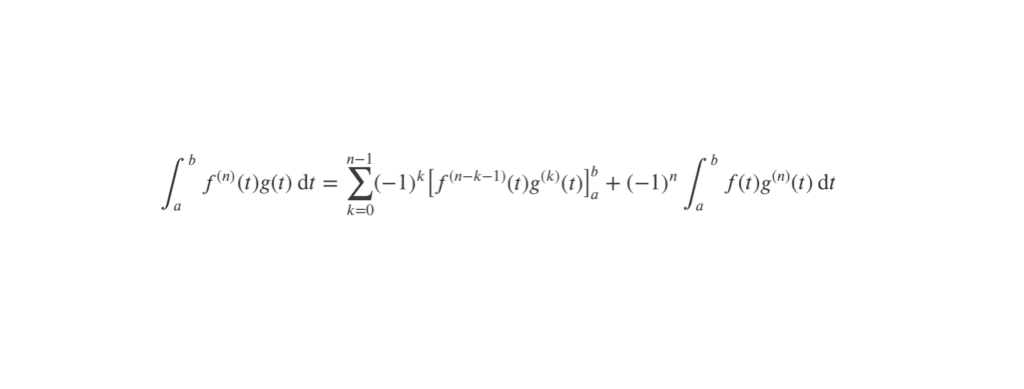
Aujourd’hui, nous allons nous intéresser à un thème classique de l’analyse : la formule d’intégration par parties itérée. Cette formule hors programme repousse les frontières de l’analyse mathématique, offrant ainsi des perspectives nouvelles sur les intégrales et leur calcul. Dans cet article, je te présente l’utilité de cette notion et plusieurs de ses propriétés qui te seront utiles lors de ta préparation aux écrits.
La formule d’intégration par parties itérée expliquée en français
L’intégration par parties itérée est une méthode utilisée pour résoudre des intégrales complexes. Elle reprend l’idée de l’intégration par parties traditionnelle en réappliquant la formule d’intégration par parties à l’intégrale qu’on obtient après une première application d’une intégration par parties.
Cela se fait de manière répétée, d’où le terme « itérée ». En procédant ainsi, on peut simplifier des intégrales complexes de manière itérative, jusqu’à obtenir une expression qui peut être résolue plus facilement.
La formule d’intégration par parties itérée
Soient \( f : [a,b] \to \mathbb{R}\) et \( g : [a,b] \to \mathbb{R}\), deux fonctions de classe \( C^n \) avec \(a < b\) deux réels et \( n \in \mathbb{N}^* \). Alors :
\[ \displaystyle\int_a^bf^{(n)}(t)g(t) \, \mathrm{d}t = \sum_{k=0}^{n-1}(-1)^k \left [ f^{(n-k-1)}(t)g^{(k)}(t)\right]_a^b + (-1)^n\int_a^bf(t)g^{(n)}(t) \, \mathrm{d}t \]
Démonstration de la formule d’intégration par parties itérée
La démonstration de cette formule est particulièrement importante, car si tu rencontres cette notion dans un sujet, il est fort probable que la première question te demande de démontrer cette égalité. De plus, la démonstration te permet de comprendre comment cette formule fonctionne.
Soient \( f : [a,b] \to \mathbb{R}\) et \( g : [a,b] \to \mathbb{R}\), deux fonctions de classe \( C^{\infty} \) avec \(a < b\) deux réels.
Montrons par récurrence sur l’entier naturel \( n \) non nul le prédicat suivant : \( P(n) :\) \( \displaystyle\int_a^bf^{(n)}(t)g(t) \, \mathrm{d}t = \sum_{k=0}^{n-1}(-1)^k \left [ f^{(n-k-1)}(t)g^{(k)}(t)\right]_a^b + (-1)^n\int_a^bf(t)g^{(n)}(t) \, \mathrm{d}t\)
Initialisation
Montrer que \( P(1) \) est vrai est équivalent à montrer que \( \displaystyle\int_a^bf^{\prime}(t)g(t) \, \mathrm{d}t = \left [ f(t)g(t)\right]_a^b -\int_a^bf(t)g^{\prime}(t) \, \mathrm{d}t \) est vrai, ce qui est bien vrai, car cette égalité est l’intégration par parties classique.
Hérédité
Supposons que \( P(n) \) est vrai pour un certain entier naturel non nul, \(n\).
\(
\begin{align}
\text{On a :}& \; \;\displaystyle\int_a^bf^{(n+1)}(t)g(t) \, \mathrm{d}t \\
&=\displaystyle\int_a^b(f^{\prime})^{(n)}(t)g(t) \, \mathrm{d}t \\
&=\sum_{k=0}^{n-1}(-1)^k \left [ (f^{\prime})^{(n-k-1)}(t)g^{(k)}(t) \right ]_a^b + (-1)^n\int_a^bf^{\prime}(t)g^{(n)}(t) \, \mathrm{d}t \; \; \text{[H.R.]} \\
& = \sum_{k=0}^{n-1}(-1)^k \left [ (f^{((n+1)-k-1)}(t)g^{(k)}(t) \right ]_a^b +(-1)^n \left ( \left [ f(t)g^{(n)}(t) \right ]_a^b -\int_a^bf(t)g^{(n+1)}(t) \, \mathrm{d}t \right ) \text{(IPP)} \\
&=\sum_{k=0}^n(-1)^k \left [ (f^{((n+1)-k-1)}(t)g^{(k)}(t) \right ]_a^b +(-1)^{n+1} \int_a^bf(t)g^{(n+1)}(t) \, \mathrm{d}t
\end{align}
\)
Ce qui est la propriété au rang suivant. Nous venons donc de démontrer la formule d’intégration par parties itérée.
Application de la formule
Essayons de calculer l’intégrale suivante : \( \displaystyle \int_0^1e^tt^n \, \mathrm{d}t \). Pour cela, utilisons la formule d’intégration par parties itérée avec \(a = 0, b = 1 \; \text{et} \; \forall t \in [0,1], f^{(n)}(t) = e^t, g(t)=t^n \)
\(
\begin{align}
\text{On a :} \displaystyle \int_0^1e^tt^n \; \mathrm{d}t &= \sum_{k=0}^{n-1}(-1)^k \frac{n!}{(n-k)!}\left [e^t t^{n-k} \right ]_0^1 +(-1)^n \int_0^1e^tn! \, \mathrm{d}t \\
&=\sum_{k=0}^{n-1} \left ((-1)^k \frac{n!}{(n-k)!}e \right ) + (-1)^nn! (e -1) \\
&=n!\left ( (-1)^{n+1} + e\left ( (-1)^n+\sum_{k=0}^{n-1} \frac{(-1)^k}{(n-k)!} \right )\right )
\end{align}
\)
Conclusion
En résumé, la formule d’intégration par parties itérée est un outil mathématique particulièrement utile en analyse qui te permet de résoudre rapidement des intégrales complexes. Ainsi, bien que cette notion soit hors programme, son étude approfondie enrichira ta préparation à toutes les épreuves de mathématiques.
Tu peux d’ailleurs t’entraîner sur le sujet Maths I 2011 (mathématiques appliquées) qui aborde le thème de l’intégration par parties itérée.
Tu peux retrouver ici toutes nos autres ressources mathématiques.
