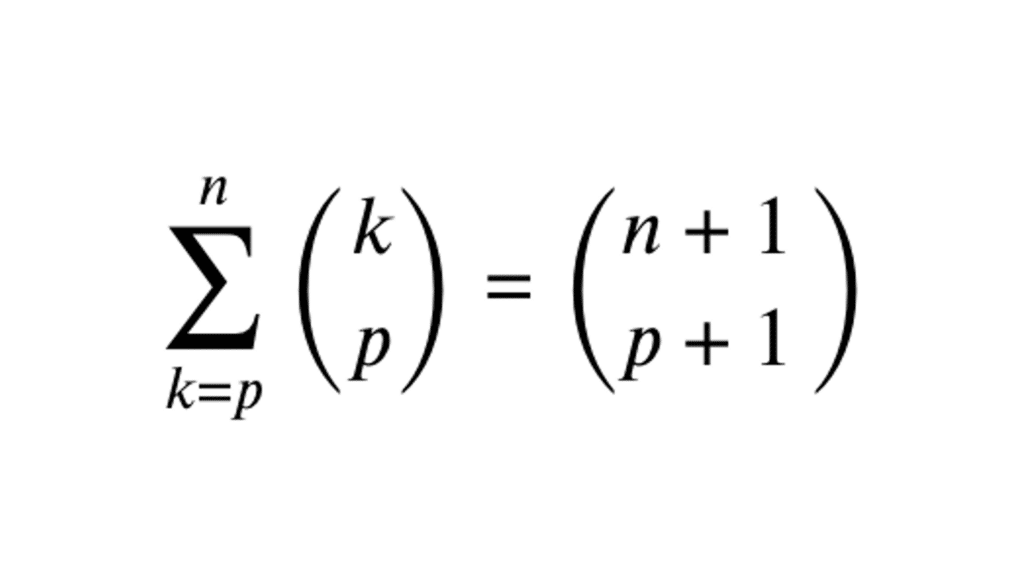La formule d’itération de Pascal est un (très) grand classique des concours ECG, que ce soit des sujets EDHEC/EM Lyon mais aussi des sujets parisiens. Elle a beau demeurer une notion en marge du programme, elle est très rapide et relativement facile à maîtriser. Cet article te propose de décortiquer cette formule d’itération de Pascal afin de t’assurer des points à ton futur DS, CB, voire concours !
Formule d’itération de Pascal
Définition
Soient \(n, p \in \mathbb{N}\) tels que \(n \geq p\), \(\displaystyle \sum_{k=p}^{n} {{k} \choose {p}} = {{n+1} \choose {p+1}}\).
Remarques :
- En utilisant la complétion du triangle de Pascal par des termes nuls, on peut aussi l’écrire : \(\displaystyle \sum_{k=0}^{n} {{k} \choose {p}} = {{n+1} \choose {p+1}}\) avec \(n, p \geq 0 \).
- Pour rappel, on sait que \(\displaystyle {{n} \choose {k}} = 0\) lorsque \(k > n\).
- En utilisant la symétrie des coefficients binomiaux, on obtient la somme d’une diagonale descendante, \(\displaystyle \sum_{k=p}^{n} {{k} \choose {k-p}} = {{n+1} \choose {p+1}}\) pour \(n \geq p \).
- Pour rappel, on sait que \(\displaystyle {{n} \choose {k}} = {{n} \choose {n-k}}\) avec \(n, k \in \mathbb{N}\) et \(n \geq k\).
Explications
La formule d’itération de Pascal, appelée aussi formule de la gouttière (ou formule de la crosse de hockey), donne le résultat d’une somme finie de termes consécutifs d’une colonne du triangle de Pascal, débutant au premier terme non nul, comme étant le coefficient binomial situé à droite et en dessous du dernier terme.
Explication graphique avec le triangle de Pascal
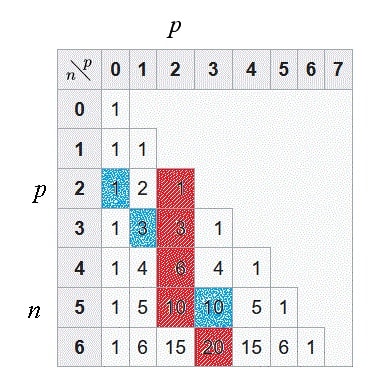
Les cases rouges sont celles utilisées par la formule pour \(n\)=5, \(p\)=2 ; en bleu, cas d’une diagonale descendante pour les mêmes valeurs.
Remarque : grâce à ce triangle de Pascal, on comprend la logique derrière le titre de « formule de la crosse de hockey ». En effet, les cases rouges, qui sont des éléments de la somme, et la case rouge 20, qui représente le résultat de la somme, forment une sorte de crosse.
Démonstrations de la formule d’itération de Pascal
Les premières démonstrations suivantes reposent sur une autre propriété de Pascal qui est au programme : \(\displaystyle {{n} \choose {k}} = {{n-1} \choose {k-1}} + {{n-1} \choose {k}}\). On l’appelle « la relation de Pascal ». Graphiquement, on voit sur le tableau ci-dessus que la somme de deux nombres consécutifs sur une même ligne est égale au nombre situé sous le second nombre additionné.
Démonstration par télescopage
\begin{align*} \displaystyle \sum_{k=p}^{n} {{k} \choose {p}} &= \sum_{k=p}^{n} \left( {{k+1} \choose {p+1}} – {{k} \choose {p+1}} \right) \text{ d’après la relation de Pascal} \\ &= \displaystyle {{p+1} \choose {n+1}} – {{p+1} \choose {p}} \text{ par télescopage} \\ &= \displaystyle {{p+1} \choose {n+1}}. \end{align*}
Remarque : cette démonstration de la formule d’itération de Pascal est la plus courte, la plus simple et la plus élégante des trois. Je la conseille fortement !
Démonstration par récurrence
Montrons que \(\displaystyle \sum_{k=p}^{n} {{k} \choose {p}} = {{n+1} \choose {p+1}}\) avec \(n, p \in \mathbb{N}\) et \(n \geq p\).
Initialisation : pour \(n\)=\(p\), on obtient 1=1
Hérédité : Soit un certain \( n \) appartenant à \([\![p, +\infty[\![\).
On a : \begin{align*} \displaystyle \sum_{k=p}^{n} {{k} \choose {p}} &= {{n+1} \choose {p+1}} \text{ par hypothèse de récurrence.} \\ \displaystyle \sum_{k=p}^{n+1} {{k} \choose {p}} &= \sum_{k=p}^{n} {{k} \choose {p}} + {{n+1} \choose {p}} \\ &= {{n+1} \choose {p+1}} + {{n+1} \choose {p}} \\ &= {{n+2} \choose {p+1}}. \end{align*}
Conclusion : la proposition est initialisée et héréditaire, donc par principe de récurrence, on a démontré la formule d’itération de Pascal.
Remarque : cette démonstration (comme la première) est rigoureuse. Cependant, comme toute récurrence, elle nécessite de connaître au préalable le résultat à démontrer. Ici, la formule d’itération de Pascal. Cela ne devrait pas poser trop de problèmes : la formule étant hors programme, il est quasiment certain que dans des sujets, on te demande « Montrer que… ».
Démonstration par itération de la relation de Pascal
\begin{align*} \text{On a } \displaystyle {{n+1} \choose {p+1}} &= {{n} \choose {p}} + {{n} \choose {p+1}} \text{ d’après la relation de Pascal.} \\ & = \displaystyle {{n} \choose {p}} + {{n-1} \choose {p}} + {{n-1} \choose {p+1}} \\ & = \displaystyle {{n} \choose {p}} + {{n-1} \choose {p}} + \dots + {{n-k} \choose {p}} + {{n-k} \choose {p+1}} \end{align*}
On pose \(k\)= \(n\) – \(p\) :
On a \(\displaystyle {{n+1} \choose {p+1}} = {{n} \choose {p}} + {{n-1} \choose {p}} + \cdots + {{p} \choose {p}} + {{p} \choose {p+1}}\) ce qui donne bien la formule voulue.
Remarque : cette démonstration peut être utile à comprendre. Cependant, je ne conseille pas de l’apprendre et de l’utiliser, car les « … » sont souvent mal vus par des correcteurs très rigoureux. Privilégie la démonstration 1 ou 2.
Remarque générale : on peut également trouver des démonstrations de la formule d’itération de Pascal qui reposent sur la formule des séries géométriques ou encore sur le dénombrement, mais mieux vaut tout de même privilégier les démonstrations n° 1 et n° 2, bien plus classiques et plus connues des correcteurs. De plus, elles ne sont pas évidentes à comprendre et pourraient causer des erreurs d’étourderie.
Utilisation de la formule d’itération de Pascal
Exemples pratiques
La formule d’itération de Pascal est particulièrement utile pour retrouver les formules des sommes des premières puissances.
Si on développe notre formule, on obtient : \[ \displaystyle \sum_{k=p}^{n} {k(k-1)\cdots(k-p+1)} = \frac{(n+1)(n)\cdots(n-p+1)}{(p+1)}. \]
Pour \(p\)=1, on obtient la somme des n premiers entiers naturels : \[ \displaystyle \sum_{k=1}^{n} k = \frac{n(n+1)}{2}. \]
Pour \(p\)=2, on trouve \[ \displaystyle \sum_{k=2}^{n} k(k-1) = \frac{n(n-1)(n+1)}{3}, \] ce qui nous permet d’obtenir par la suite la somme des n premiers carrés qui vaut \[ \displaystyle \sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6}. \]
Et pour \(p\)=3, \(p\)=4…
Une chose est sûre, si dans un sujet, on te fait démontrer la formule d’itération de Pascal, c’est qu’il faudra l’utiliser dans les questions suivantes. Donc, reste à l’affût !
Applications réelles
La formule d’itération de Pascal est appliquée dans divers domaines pour simplifier les calculs combinatoires et optimiser les algorithmes :
- En analyse combinatoire, pour déterminer la somme des coefficients binomiaux et faciliter le comptage des sous-ensembles.
- En informatique, pour optimiser les algorithmes et simplifier les expressions de complexité.
- En probabilité et statistique, pour calculer les espérances et les variances des variables aléatoires combinatoires.
- En théorie des graphes, pour compter les chemins et cycles.
- En génétique, pour analyser les combinaisons de traits.
- En économie et recherche opérationnelle, pour modéliser et optimiser des décisions et des systèmes.
Somme des inverses des termes d’une colonne du triangle de Pascal
Pour \( \displaystyle n \geq p \geq 2 \),
\[ \displaystyle \sum_{k=p}^{n} \frac{1}{\displaystyle {k \choose p}} = \frac{p}{p-1} \left(1 – \frac{1}{\displaystyle {n \choose p-1}}\right) \]
Donc, \[ \displaystyle \sum_{k=p}^{\infty} \frac{1}{\displaystyle {k \choose p}} = \frac{p}{p-1} \] On arrive au résultat précédent car \[ \displaystyle \sum_{k=p}^{\infty} \frac{1}{\displaystyle {k \choose p}} = \displaystyle \sum_{k=p}^{n} \frac{1}{\displaystyle {k \choose p}} + \displaystyle \sum_{k=n+1}^{\infty} \frac{1}{\displaystyle {k \choose p}} \]
et par télescopage à partir de \[ \displaystyle \frac{1}{\displaystyle {k \choose p}} = \frac{p}{p-1} \left( \frac{1}{\displaystyle {k-1 \choose p-1}} – \frac{1}{\displaystyle {k \choose p-1}} \right) \] qui provient de la relation : \[ \displaystyle (p-1) {k-1 \choose p-1} {k \choose p-1} = p {k-2 \choose p-1} {k \choose p} \]
Finalement, on peut écrire la somme de la façon suivante : \[ \displaystyle \sum_{k=p}^{\infty} \frac{1}{k(k-1)\cdots (k-p+1)} = \frac{1}{(p-1)!(p-1)} \]
Sujet invoquant la démonstration de l’itération de Pascal
Conclusion
Maintenant, tu maîtrises la formule d’itération de Pascal, tu es capable de démontrer cette relation et tu comprends ses applications variées ! Bien que cette notion puisse ne pas être au programme, sa compréhension te sera précieuse si tu rencontres des problèmes combinatoires complexes. Nous espérons que cet article de Major-prépa t’a apporté des éclaircissements et qu’il a enrichi ta compréhension des outils combinatoires.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !