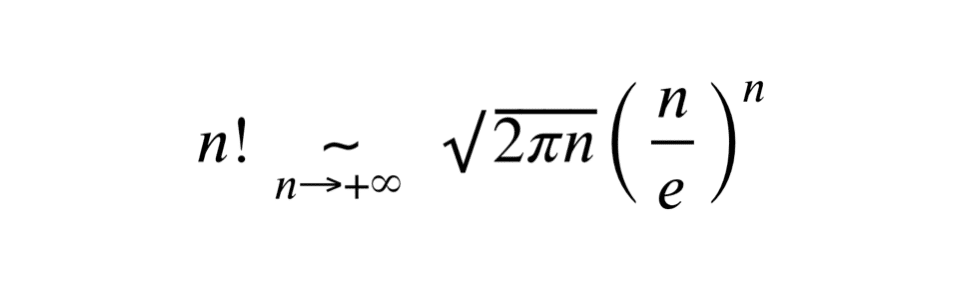En mathématiques, la formule de Stirling est une approximation puissante qui permet d’estimer la factorielle d’un nombre entier \(n\). Cette formule, qui se traduit à l’aide d’un équivalent, est donc particulièrement utile lorsque \(n\) est grand, car le calcul direct de \(n!\) devient rapidement impraticable à mesure que \(n\) augmente. James Stirling, un mathématicien écossais du XVIIIe siècle, est crédité de cette découverte, qui joue un rôle crucial en statistique, en analyse combinatoire et dans d’autres domaines des mathématiques appliquées. Bien que cette formule soit hors programme, elle tombe régulièrement aux concours. Ainsi, la maîtrise de sa démonstration et de ses propriétés te permettra de te préparer au mieux aux épreuves parisiennes et aux oraux de mathématiques.
Qu’est-ce que la formule de Stirling ?
La formule de Stirling fournit une approximation, plus précisément un équivalent de la factorielle d’un grand nombre par l’expression suivante :
\[ \fbox{\( \displaystyle n! \underset{n \to +\infty}{\sim} \sqrt{2\pi n} \left( \frac{n}{e} \right)^n \)}\]
Où \(e\) est la constante d’Euler. Cette formule est remarquable, car elle donne une estimation très proche de la valeur exacte de \(n!\), surtout pour les grandes valeurs de \(n\).
Importance et applications de la formule de Stirling
L’importance de la formule de Stirling réside dans sa capacité à simplifier les calculs impliquant des factorielles, particulièrement dans le contexte des probabilités et des statistiques.
Par exemple, elle est utilisée dans l’approximation de distributions, comme la distribution binomiale par la distribution normale dans le théorème central limite, un fondement de la statistique.
Démonstration de la formule de Stirling
Une des manières de démontrer la formule de Stirling est d’utiliser les intégrales de Wallis, qui ne sont pas au programme de ECG, mais qui reviennent régulièrement dans les sujets de concours.
Elles fournissent un lien entre les produits de factorielles et les intégrales définies.
Les intégrales de Wallis
Les intégrales de Wallis sont une suite d’intégrales pouvant être exprimées comme suit : \[ W_{n} = \int_{0}^{\pi/2} \sin^n(x) \mathrm{d}x \]
Démonstration via les intégrales de Wallis
En exploitant les propriétés des intégrales de Wallis, on peut établir une relation entre ces intégrales et les factorielles. Ce qui sert de pont pour atteindre la formule de Stirling. La démarche implique des techniques d’intégration avancées et des manipulations algébriques pour relier \(W_{n}\) à \(n!\).
En utilisant une récurrence et des intégrations par parties, on peut montrer que :
\[ \fbox{ \(W_{2n} = \frac{\pi}{2} \frac{(2n)!}{2^{2n}(n!)^2} \; \text{et} \; W_{2n+1}=\frac{2^{2n}(n!)^2}{(2n+1)!}\)} \]
En utilisant ces formules et en déduisant que \(W_{2n}\) est équivalent à \(W_{2n+1}\) avec la formule \((n+2)W_{n+2}=(n+1)W_n\), on obtient finalement la formule de Stirling.
Application de la formule de Stirling
Outre les applications directes de la formule de Stirling dans l’approximation de factorielles, une propriété mathématique notable concerne son utilisation pour approcher des sommes et des séries.
En particulier, la formule de Stirling permet de simplifier et d’estimer le comportement asymptotique de séries impliquant des factorielles. Un exemple frappant est l’approximation des coefficients binomiaux, largement utilisés en combinatoire et en théorie des probabilités.
Considérons le coefficient binomial \({{n}\choose{k}}\), qui peut être exprimé à l’aide des factorielles comme suit :
\[
{{n}\choose{k}} = \frac{n!}{k!(n-k)!}
\]
En appliquant la formule de Stirling à chaque factorielle dans cette expression, donc lorsque \(k \; \text{et} \; n \) se rapprochent de \( +\infty\), nous obtenons :
\[
{{n}\choose{k}} \sim \frac{\sqrt{2\pi n}\left(\frac{n}{e}\right)^n}{\sqrt{2\pi k}\left(\frac{k}{e}\right)^k \sqrt{2\pi (n-k)}\left(\frac{n-k}{e}\right)^{n-k}}
\]
Simplification ultérieure, en utilisant des propriétés des exponentielles et des racines carrées, cela nous mène à :
\[
{{n}\choose{k}} \sim \frac{1}{\sqrt{2\pi k \frac{n-k}{n}}} \cdot \left(\frac{n^n}{k^k (n-k)^{n-k}}\right)
\]
Cette approximation est particulièrement utile pour analyser le comportement des coefficients binomiaux pour de grands \(n\), où les calculs directs deviennent impraticables. Elle souligne la puissance de la formule de Stirling dans l’analyse asymptotique, offrant une fenêtre sur le comportement des séries et des sommes impliquant des factorielles à de grandes échelles.
Cette propriété enrichit ta boîte à outils mathématique. Elle te permet de traiter des problèmes complexes en combinatoire, analyse, avec une plus grande facilité et une précision.
Lien avec la fonction gamma et généralisation
La formule de Stirling est étroitement liée à la fonction gamma, qui est une extension des factorielles aux nombres réels et complexes.
La fonction gamma
La fonction gamma, notée \(\Gamma(z)\), est définie pour les nombres réels par l’intégrale suivante :
\[ \Gamma(z) = \int_{0}^{\infty} t^{z-1}e^{-t} \mathrm{d}t \]
Pour tout entier naturel \(n\), on a la relation : \(\Gamma(n+1) = n!\). Ce résultat peut se démontrer avec une récurrence et une intégration par parties.
La beauté de la fonction gamma réside dans sa capacité à généraliser la notion de factorielle au-delà des entiers naturels. C’est-à-dire aux réels.
Extension de l’approximation de Stirling aux nombres réels
Grâce à la fonction gamma, l’approximation de Stirling peut être étendue aux nombres réels et complexes, offrant ainsi une généralisation puissante. Cette extension permet de calculer des approximations de \(\Gamma(z)\) pour des valeurs non entières de \(z\), élargissant le champ d’application de la formule.
En effet, l’approximation de Stirling peut être réécrite en termes de la fonction gamma comme : \(\Gamma(n+1) \sim \sqrt{2\pi n} \left( \frac{n}{e} \right)^n\)
Cet équivalent peut se généraliser dans un contexte plus large avec les nombres réels. L’extension s’exprime donc de la façon suivante : \(\int_{0}^{\infty} t^{z}e^{-t} \mathrm{d}t\sim \sqrt{2\pi z} \left( \frac{z}{e} \right)^z\)
Conclusion
La formule de Stirling est plus qu’une simple approximation mathématique. C’est un outil essentiel qui traverse de nombreux domaines des mathématiques. Sa démonstration, en particulier à travers les intégrales de Wallis, met en lumière les liens profonds entre l’analyse, la combinatoire et la théorie des probabilités. L’association avec la fonction gamma et l’extension aux nombres réels démontrent la richesse et l’universalité de cette formule mathématique.
Ainsi, cette formule et ses applications sont indispensables pour les étudiants en classes préparatoires, non seulement pour réussir les épreuves parisiennes, mais aussi pour réussir les oraux de mathématiques et les épreuves EDHEC et EML.
Pour t’entraîner sur cette notion, tu peux faire le sujet Maths II 2017 (mathématiques approfondies). Tu peux également retrouver ici toutes nos autres ressources mathématiques.