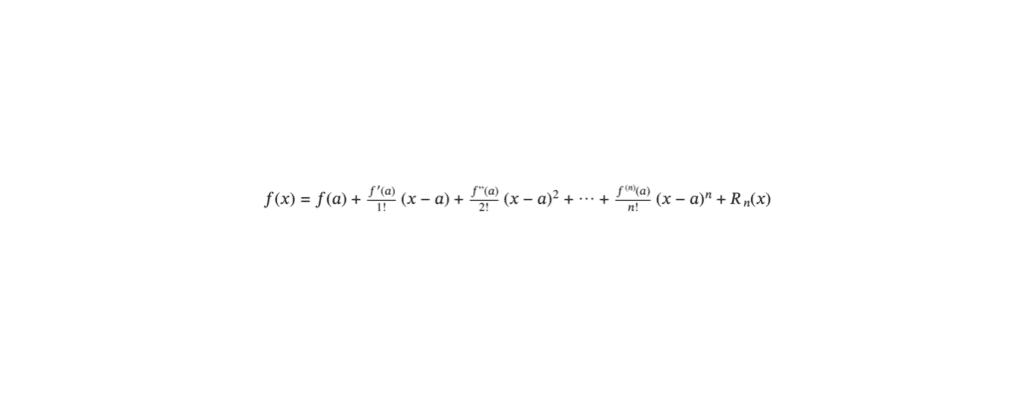On va travailler ensemble sur une formule mathématique essentielle (hors programme) : la formule de Taylor. Cette formule se retrouvant dans de nombreux sujets de concours, il est important de maîtriser ses caractéristiques. C’est aussi l’occasion pour toi de revoir les méthodes des développements limités et d’approfondir tes connaissances en analyse.
Introduction sur Taylor
Pour ta culture, Brook Taylor (1685-1731) était un mathématicien britannique de renom. La formule de Taylor, qu’il a introduite en 1715, est désormais un outil fondamental dans de nombreux domaines, y compris dans l’ingénierie.
Ses travaux ont également contribué à une meilleure compréhension des équations différentielles et des approximations locales des fonctions.
Présentation de la formule de Taylor en français
La formule de Taylor, également connue sous le nom de théorème de Taylor, est un outil mathématique essentiel qui permet d’approximer une fonction plusieurs fois dérivable au voisinage d’un point en la développant sous forme de polynôme.
La formule de Taylor exprime donc une fonction \( f(x) \) comme la somme des dérivées successives évaluées en un point \( a \), multipliées par des puissances de \( (x-a) \) auquel on ajoute un reste \( R_n(x) \). Ce dernier terme \( R_{n}(x) \) correspond à l’erreur d’approximation et est une fonction négligeable par rapport à \( (x-a)^{n} \) au voisinage de \( a \).
Présentation de la formule de Taylor en mathématiques
La formule de Taylor peut s’écrire de deux façons équivalentes.
Soient \( I \) un intervalle de \( \mathbb{R} \), \( a \) un point appartenant à \( I \), et \( f \) une fonction de \( I \) vers \( \mathbb{R} \). Soit \( n \) un entier naturel que l’on fixe. Toute fonction \( f \) de classe \( {C}^n \) sur \( I \) admet alors au voisinage du point \( a \) :
\( f(x) = f(a) + \frac{f'(a)}{1!}\,(x-a) + \frac{f”(a)}{2!}\,(x-a)^{2} + \cdots + \frac{f^{(n)}(a)}{n!}\,(x-a)^{n} + R_{n}(x)\)
\( \displaystyle f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(a)}{k!}\,(x-a)^{k} + R_{n}(x) \)
Remarque : pour rappel, une fonction \( f \) est dite de classe \( {C}^n \) sur \( I \) si elle est dérivable jusqu’à l’ordre \( n \) sur \( I \) et si sa dérivée d’ordre \( n \) est continue sur \( I \).
Lien avec la formule de Taylor-Young et les développements limités
Formule de Taylor-Young (programme ECG)
La formule de Taylor-Young est une extension de la formule de Taylor. En effet, elle exprime ce reste \( R_{n}(x) \), sous forme d’une fonction négligeable par rapport à \( (x – a)^n \) lorsque \( x \) se rapproche de \( a \). Ainsi, on a :
\( R_n(x) = o\left((x – a)^n\right) \)
Ce qui est similaire à :
\( \displaystyle \lim _{x\to a \atop x\neq a} \frac{R_{n}(x)}{(x-a)^{n}} = 0 \)
Les développements limités (programme ECG)
Pour rappel, un développement limité est une approximation d’une fonction \( f \) au voisinage d’un point sous une forme polynomiale. Il s’agit donc bien d’une application directe de la formule de Taylor-Young. Toutefois, grâce à la formule de Taylor, on va au-delà des développements limités d’ordre 2 (exigé par le programme officiel).
Exemple : tu es désormais capable de donner le développement limité d’ordre 4 au voisinage de 0 de la fonction exponentielle, qui est de classe \( C^\infty \) donc aussi de classe \( {C}^4 \). Faisons-le ensemble !
La formule de Taylor à l’ordre 4 pour une fonction \( f(x) \) autour d’un point \( a \) est :
\(\displaystyle f(x) \approx f(a) + f'(a)(x – a) + \frac{f”(a)}{2!}(x – a)^2 + \frac{f”'(a)}{3!}(x – a)^3 + \frac{f^{(4)}(a)}{4!}(x – a)^4 \)
Avec les dérivées successives de la fonction exponentielle, on a donc après calculs :
\(\displaystyle f(x) \approx 1 + 1 \cdot (x – 0) + \frac{1}{2!}(x – 0)^2 + \frac{1}{3!}(x – 0)^3 + \frac{1}{4!}(x – 0)^4 \)
Ainsi, le développement limité d’ordre 4 au voisinage de 0 de la fonction exponentielle est :
\(\displaystyle e^x \approx 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} \)
Tu peux maintenant t’entraîner à donner le développement limité d’ordre 4 au voisinage de 0 des deux fonctions suivantes :
- \( f(x) = \ ln(1+x) \)
- \( f(x) = (1+x)^\alpha \)
Formule de Taylor avec reste intégral
La formule de Taylor est également utilisée sous une forme spécifique où le reste \( R_n(x) \) est exprimé par une intégrale. Si la fonction \( f \) est de classe \( \mathcal{C}^{n+1} \) sur \( I \), alors, pour tout \( x \in I \) :
\( \displaystyle f(x) = f(a) + f'(a)(x – a) + \frac{f”(a)}{2!}(x – a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x – a)^n + \frac{1}{n!} \int_a^x (x – t)^n f^{(n+1)}(t) \, dt \)
L’intérêt de cette formule est donc de pouvoir quantifier l’erreur d’approximation, c’est-à-dire le reste \( R_n(x) \) et de vérifier si l’approximation est suffisamment précise.
La série de Taylor
Promis, c’est la dernière formule à connaître sur ce sujet !
Si tu as compris la formule de Taylor, la série de Taylor n’est en réalité qu’un prolongement de cette dernière, mais à l’infini. En effet, la série de Taylor d’une fonction infiniment dérivable en un point \( a \) est une approximation de cette fonction comme une somme infinie de termes polynomiaux. Cependant, lorsqu’on fait tendre le \( n \) vers l’infini, le reste \( R_n(x) \) devient négligeable.
Elle s’exprime ainsi :
\( \displaystyle f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} \cdot (x – a)^n \)
Utiliser la formule de Taylor en langage Python
Les sujets de concours faisant de plus en plus intervenir des exercices avec du Python, il peut être utile de maîtriser la formule de Taylor aussi dans ce langage. Le mieux est ici de s’intéresser à la série de Taylor en prenant par exemple la fonction exponentielle. L’idée est alors d’écrire un code en langage Python pour approximer la fonction exponentielle au voisinage de 0.
On veut donc écrire :
\( e^x = \displaystyle \sum_{n=0}^{\infty} \frac{x^n}{n!} \) qui se traduit aussi par \( e^x \approx 1 + x + \frac{x^2}{2!} +\ frac{x^3}{3!} + \cdots + \frac{x^n}{n!} \)
Attends, mais il ne s’agirait pas justement de la (bien connue) série exponentielle ?
On a donc, en langage Python :
Remarque : inutile de connaître ce code Python par cœur, mais tu peux essayer de le comprendre au cas où il te serait demandé de compléter des codes similaires dans un sujet de concours. Tu peux par ailleurs retrouver ici tous nos autres articles consacrés au langage Python.
Annales où tu pourras retrouver la formule de Taylor
Cette formule est d’autant plus utile à travailler qu’elle est déjà tombée de nombreuses fois aux concours de maths appliquées. Je te mets les liens des sujets où tu pourras retrouver cette formule :
- Maths I HEC 2003 Problème Partie A (question 4)
- Maths II ESSEC 2013 Partie II (question 6)
Et tu peux retrouver ici les corrigés de ces sujets :
Remarque : plus globalement, les développements limités se retrouvent dans de nombreux sujets et comprendre la formule de Taylor t’aidera désormais à les aborder avec confiance.
Conclusion
Tu connais maintenant tout sur la formule de Taylor ! Tu es désormais capable de donner cette formule (et ses autres formules spécifiques) et de l’utiliser lorsque tu en auras besoin (le plus souvent pour trouver des développements limités, tu l’as compris). Tu es même capable d’utiliser la formule de Taylor dans le langage Python.
Tu peux retrouver ici toutes nos autres ressources mathématiques et continuer à t’exercer sur d’autres annales grâce à notre méga-répertoire.