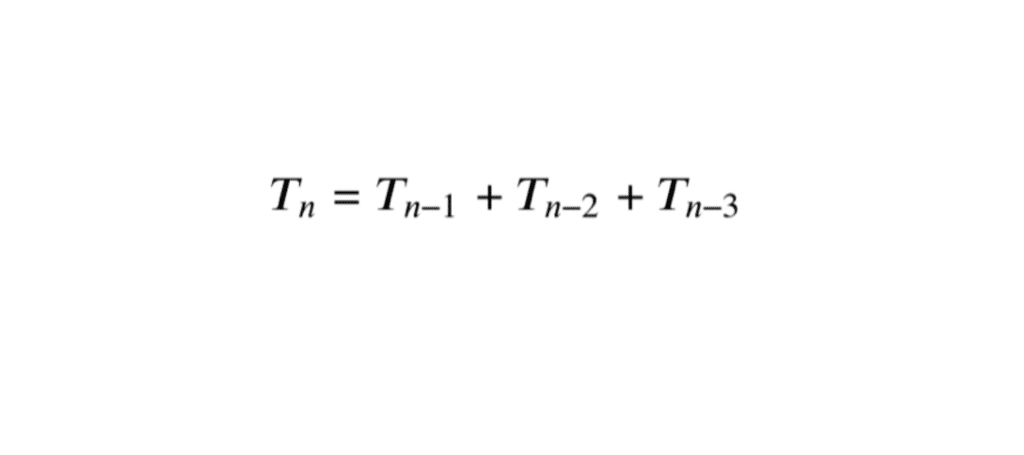La suite de Fibonacci (du mathématicien Leonardo Fibonacci) est l’une des suites les plus célèbres en mathématiques, connue pour ses propriétés fascinantes et ses nombreuses applications. Cependant, il existe des généralisations de cette suite qui permettent d’explorer des structures mathématiques plus riches et diversifiées. Cet article se propose de présenter plusieurs généralisations de la suite de Fibonacci, en détaillant leurs propriétés et leurs applications. Nous examinerons la suite de Lucas, les \(k\)-suites de Fibonacci (aussi appelées les suites de \(k\)-bonacci) et les suites de Fibonacci généralisées à partir de relations de récurrence plus complexes.
Définition et propriétés de la suite de Fibonacci
En mathématiques, la suite de Fibonacci est définie par récurrence de la manière suivante :
\[ F_0 = 0, \; F_1 = 1 \; \text{et} \; F_n = F_{n-1} + F_{n-2}, \quad \text{pour tout entier } n \geq 2
\]
Autrement dit, les deux valeurs de départ 0 et 1 étant données, chaque nombre est la somme des deux précédents. La suite de Fibonacci peut être généralisée de nombreuses façons. Par exemple, en partant d’autres nombres que 0 et 1, en ajoutant plus de deux termes pour engendrer le suivant…
Extension aux entiers négatifs
À l’aide de la relation \( F_{n-2} = F_n – F_{n-1} \), on peut étendre la suite de Fibonacci à des indices entiers négatifs. On obtient la suite :
\[
\ldots, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, \ldots
\]
qui vérifie : \( F_{-n} = (-1)^{n+1} F_n \).
Augmentation de l’ordre de la récurrence
Une suite de type Fibonacci d’ordre \( p \), ou suite de \( p \)-bonacci, est une suite d’entiers dans laquelle chaque terme à partir du \( p+1 \)-ième est la somme des \( p \) précédents (le cas classique est \( p = 2 \)).
Exemples et propriétés
1. Tribonacci (p=3) :
\[
T_n = T_{n-1} + T_{n-2} + T_{n-3}
\]
avec \( T_0 = 0, T_1 = 0, T_2 = 1 \).
2. Tetranacci (p=4) :
\[
Tet_n = Tet_{n-1} + Tet_{n-2} + Tet_{n-3} + Tet_{n-4}
\]
avec \( Tet_0 = 0, Tet_1 = 0, Tet_2 = 0, Tet_3 = 1 \).
Propriétés des \(k\)-suites de Fibonacci (ou les suites de \(k\)-bonacci)
Les \(k\)-suites de Fibonacci présentent des propriétés intéressantes, notamment en termes de croissance. Comme pour la suite de Fibonacci classique, les termes des \(k\)-suites de Fibonacci croissent de manière exponentielle, mais avec un taux de croissance plus élevé.
La formule de Binet généralisée pour les \(k\)-suites de Fibonacci peut être exprimée à l’aide des racines du polynôme caractéristique :
\[
x^k – x^{k-1} – x^{k-2} – \cdots – x – 1 = 0
\]
Les solutions de cette équation caractéristique donnent les valeurs propres \(\lambda_1, \lambda_2, \ldots, \lambda_k\). La formule de Binet généralisée est alors :
\[
F_n^{(k)} = a_1 \lambda_1^n + a_2 \lambda_2^n + \cdots + a_k \lambda_k^n
\]
où \(a_1, a_2, \ldots, a_k\) sont des coefficients déterminés par les conditions initiales.
Modification des coefficients de la récurrence
En reprenant les notations des suites de Fibonacci, on peut considérer les suites \( (u_n) \) vérifiant \( u_{n+2} = p u_{n+1} – q u_n \) où \( p \) et \( q \) sont des entiers fixés. Elles sont toutes des combinaisons linéaires des deux suites de base \( (U_n) \), \( (V_n) \) définies par :
\[
U_0 = 0, \quad U_1 = 1, \quad U_{n+2} = p U_{n+1} – q U_n
\]
\[
V_0 = 2, \quad V_1 = p, \quad V_{n+2} = p V_{n+1} – q V_n
\]
Pour \( p = 1, q = -1 \), \( U_n = F_n \) et \( V_n = L_n \), où \( L_n \) est la suite de Lucas.
Lorsque \( q = -1 \), la suite \( (U_n) \) est appelée \( p \)-suite de Fibonacci et c’est aussi la valeur en \( p \) du polynôme de Fibonacci d’indice \( n \).
Exemples de suites généralisées
1. La 2-suite de Fibonacci (suite de Pell) :
\(
0, 1, 2, 5, 12, 29, 70, 169, 408, 985, \ldots
\)
2. La 3-suite de Fibonacci :
\(
0, 1, 3, 10, 36, 136, 528, 2080, \ldots
\)
3. La 4-suite de Fibonacci :
\(
0, 1, 4, 15, 64, 280, 1260, 5736, \ldots
\)
Suite de Lucas
La suite de Lucas est une généralisation directe de la suite de Fibonacci. Elle est définie par une relation de récurrence similaire, mais avec des conditions initiales différentes. La suite de Lucas \(L_n\) est définie par :
\[
L_n = L_{n-1} + L_{n-2}
\]
avec \(L_0 = 2\) et \(L_1 = 1\). Les premiers termes de la suite de Lucas sont : 2, 1, 3, 4, 7, 11, 18…
La suite de Lucas partage de nombreuses propriétés avec la suite de Fibonacci. Par exemple, la relation de récurrence permet de démontrer que :
\[
L_n = \varphi^n + \overline{\varphi}^n
\]
où \(\varphi\) et \(\overline{\varphi}\) sont les mêmes valeurs propres que celles utilisées pour la suite de Fibonacci. Cette formule montre que la suite de Lucas peut être exprimée en termes des nombres d’or et de leurs conjugués, tout comme la suite de Fibonacci.
La suite de Pell
La suite de Pell est une généralisation intéressante de la suite de Fibonacci, définie par une relation de récurrence spécifique. Plus précisément, la suite de Pell \((P_n)\) est définie par \( P_0 = 0 \), \( P_1 = 1 \) et pour \( n \geq 2 \), \( P_n = 2P_{n-1} + P_{n-2} \). Cette suite croît plus rapidement que la suite de Fibonacci en raison du coefficient multiplicatif 2 dans la relation de récurrence. Les premiers termes de la suite de Pell sont :
\[
0, 1, 2, 5, 12, 29, 70, 169, 408, 985, \ldots
\]
Une propriété remarquable de cette suite est qu’elle est étroitement liée aux nombres de Pell, qui apparaissent dans la résolution des équations de Pell, une classe d’équations diophantiennes de la forme :
\[
x^2 – 2y^2 = 1
\]
La suite de Pell a également des applications en théorie des nombres et en algèbre, notamment dans l’étude des fractions continues et des approximations des racines carrées de 2.
La suite de Tribonacci
La suite de Tribonacci est une autre généralisation intéressante de la suite de Fibonacci. Elle est définie par une relation de récurrence où chaque terme est la somme des trois termes précédents, au lieu de deux. Plus précisément, la suite de Tribonacci \((T_n)\) est définie par \( T_0 = 0 \), \( T_1 = 0 \), \( T_2 = 1 \) et pour \( n \geq 3 \), \( T_n = T_{n-1} + T_{n-2} + T_{n-3} \). Les premiers termes de la suite de Tribonacci sont :
\[
0, 0, 1, 1, 2, 4, 7, 13, 24, 44, \ldots
\]
Comme la suite de Fibonacci, la suite de Tribonacci possède une formule de Binet généralisée. Elle est liée aux racines du polynôme caractéristique cubique :
\[
x^3 – x^2 – x – 1 = 0
\]
Les racines de ce polynôme, appelées valeurs propres de la suite de Tribonacci, permettent d’exprimer chaque terme \( T_n \) comme une combinaison linéaire de ces racines élevées à la puissance \( n \). La suite de Tribonacci trouve des applications dans diverses branches des mathématiques et de la science, telles que la combinatoire, la théorie des graphes et la dynamique des populations. Par exemple, elle peut modéliser des processus où un événement dépend des trois événements précédents, offrant ainsi une perspective plus riche et complexe que la suite de Fibonacci classique.
Aller plus loin
Les suites de \(k\)-bonacci sont à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour (et de la suite de Fibonacci) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) | |
| Suites | Nombres |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Un autre type de généralisation de la suite de Fibonacci est également à découvrir ! Il s’agit de la suite de Fibonacci aléatoire. Elle pourrait clairement faire l’objet d’un sujet de maths parisienne dans les années à venir…
A lire également : le triangle de Pascal (et ses liens avec la suite de Fibonacci).
Conclusion
Les généralisations de la suite de Fibonacci offrent un terrain riche pour l’exploration mathématique. En étendant les idées simples de la suite de Fibonacci classique, nous découvrons des structures mathématiques complexes et des applications diverses. Que ce soit à travers la suite de Lucas, les \( k \)-suites de Fibonacci ou les suites de Fibonacci généralisées, ces généralisations enrichissent notre compréhension des relations récurrentes et de leurs propriétés.
Ainsi, bien que la généralisation de la suite de Fibonacci soit hors programme, la compréhension approfondie de cette notion te permettra d’améliorer tes compétences en algèbre et en analyse. L’étude de cette notion te préparera donc pour les épreuves écrites et orales. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies),
- Maths 1 HEC 2009 (mathématiques appliquées),
- la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !