Les graphes ont récemment fait leur entrée dans le programme officiel de prépa HEC pour les Maths Appliquées. Ils ont notamment été l’objet du Sujet 0 de HEC 2023, et je t’invite ici à découvrir le cours complet sur les graphes.
Histoire des mathématiques et utilité des graphes
Les graphes sont des structures mathématiques qui ont une longue histoire et ont trouvé de nombreuses applications dans divers domaines. Ils ont été introduits pour la première fois par le mathématicien suisse Leonhard Euler au XVIIIe siècle pour résoudre le problème des sept ponts de Königsberg.
Depuis lors, les graphes ont été utilisés dans la théorie des réseaux, l’optimisation, la planification, la modélisation de systèmes complexes, les réseaux sociaux, etc. Leur simplicité et leur puissance en font un outil fondamental pour l’analyse de problèmes complexes.
Définitions et vocabulaire
Vocabulaire ensembliste
Avant tout, il convient de s’y retrouver dans les sigles « singleton », « paire » et « couple » d’éléments d’un ensemble \(E\).
Singleton : ensemble qui ne contient qu’un seul élément. Formellement, si \(“x”\) est un élément de l’ensemble \(E\), alors le singleton contenant \(“x”\) est l’ensemble noté {\(x\)}.
Paire : ensemble qui contient exactement deux éléments distincts. Formellement, si \(“x”\) et \(“y”\) sont deux éléments distincts de l’ensemble \(E\), alors la paire contenant \(“x”\) et \(“y”\) est notée {\(x, y\)}.
Couple : généralisation de la notion de paire qui permet d’inclure le cas où les deux éléments peuvent être identiques (ils peuvent être égaux). Formellement, si “\(x\)” et “\(y\)” sont deux éléments (peuvent être identiques) de l’ensemble \(E\), alors le couple contenant \(“x”\) et \(“y”\) est noté (\(x, y)\).
Il est important de noter que l’ordre des éléments, tout comme le caractère répétitif des éléments dans un couple (et non dans une paire) est significatif. Par exemple, \((x, y)\) est différent de \((y, x)\), sauf si \(x = y\). Par contre, {\(x,y\)} et {\(y,x\)} représentent le même sous-ensemble de l’ensemble \(E\).
Définitions liées aux graphes
Graphes orientés et non orientés
Un graphe est un ensemble de points, appelés sommets (ou nœuds), reliés par des lignes, appelées arêtes (ou arcs). On distingue deux types de graphes :
- les graphes non orientés : les arêtes n’ont pas de direction, ce qui signifie que la relation entre les sommets est symétrique. Si un sommet \(A\) est relié à un sommet \(B\), alors \(B\) est également relié à \(A\) ;
- les graphes orientés : les arêtes ont une direction (on dira « arêtes orientées »), ce qui signifie que la relation entre les sommets est asymétrique. Si un sommet \(A\) est relié à un sommet \(B\), cela ne signifie pas nécessairement que \(B\) est relié à \(A\).
Définition d’un graphe
Un graphe fini orienté est la donnée :
1. D’un ensemble fini non vide de sommets (= de points) \(\mathcal{S}\).
2. D’un ensemble d’arêtes orientées \(\mathcal{A}\), dont les éléments sont des couples d’éléments de \(\mathcal{S}\).
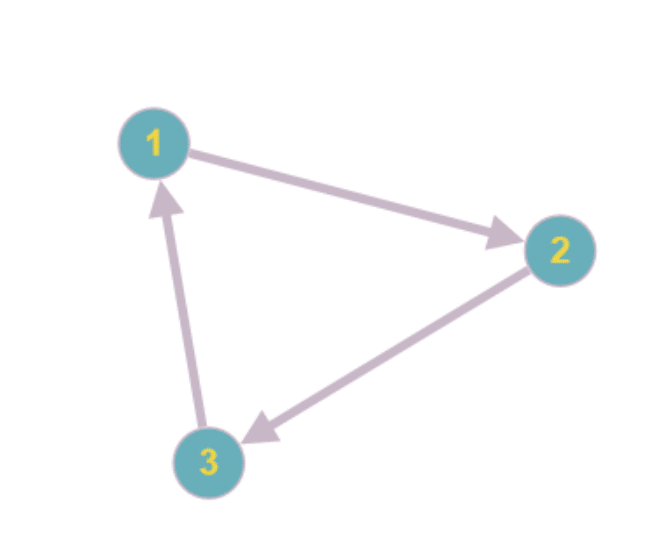
Exemple : \(\mathcal{G}\)=(\(\mathcal{S}\),\(\mathcal{A}\)), avec \(\mathcal{S}=\){\(1,2,3\)}, et \(\mathcal{A}=\){\((1,2),(2,3),(3,1)\)} est un graphe orienté à \(3\) sommets ayant \(3\) arêtes orientées.
Un graphe fini non orienté est la donnée :
1. D’un ensemble fini non vide de sommets \(\mathcal{S}\).
2. D’un ensemble d’arêtes \(\mathcal{A}\), dont les éléments sont des paires d’éléments de \(\mathcal{S}\).
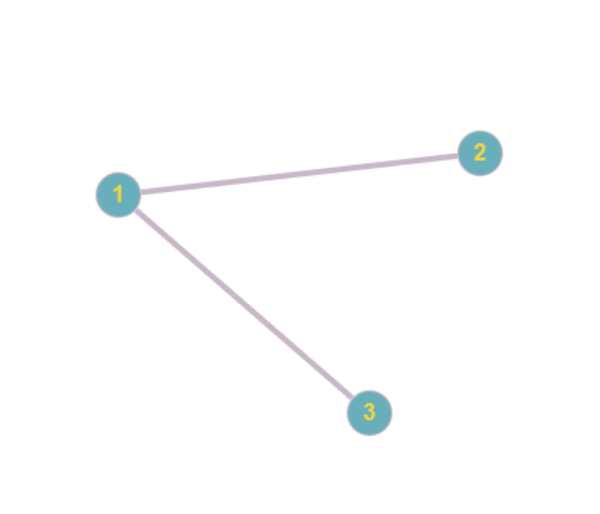
Exemple : \(\mathcal{G}\)=(\(\mathcal{S}\),\(\mathcal{A}\)), avec \(\mathcal{S}=\) {\(1,2,3\)}, et \(\mathcal{A}=\){{\(1,2\)}, {\(3,1\)}} est un graphe non orienté à \(3\) sommets ayant \(2\) arêtes.
Vocabulaire lié aux graphes
Sommets adjacents : deux sommets \((t,s)\) appartenant à \(\mathcal{S}\) sont adjacents si {\(t,s\)} \( \ \text{ou} \ (t,s) \ \text{ou} \ (s,t)\) (selon que le graphe est orienté ou non) appartient à \(\mathcal{A}\).
Sommet isolé : un sommet est dit isolé s’il n’est relié à aucun autre sommet par une arête (dans un graphe non orienté).
Extrémités d’une arête ou d’un arc : les extrémités d’une arête dans un graphe sont les sommets qui sont reliés par cette arête (orientée ou non).
Boucle : une boucle est une arête définie par un seul sommet dans un graphe non orienté (ou une arête orientée définie par un couple de même sommet dans un graphe orienté). En d’autres termes, une boucle relie un sommet à lui-même.
Graphe simple : un graphe est dit simple s’il ne contient pas de boucles et si chaque paire de sommets distincts est reliée par au plus une arête.
Ordre d’un graphe fini : l’ordre d’un graphe fini est le nombre de sommets qu’il contient. Il représente le nombre total de sommets présents dans le graphe.
Représentation graphique
Pour représenter un graphe, on peut utiliser des schémas ou des diagrammes, où les sommets sont représentés par des cercles ou des points et les arêtes sont représentées par des lignes (si non orienté) ou des flèches (si orienté) entre les sommets.
Pour reprendre les graphes définis plus haut, on a le graphe orienté qui se représente ainsi :
Et le graphe non orienté qui se représente ainsi :
Matrice d’adjacence
La matrice d’adjacence est une représentation matricielle d’un graphe. Pour un graphe non orienté à \(n\) sommets, la matrice d’adjacence est une matrice carrée de taille \(n \times n\). Chaque élément de la matrice est soit \(0\) si les sommets correspondants ne sont pas reliés par une arête, soit \(1\) s’ils sont reliés par une arête.
Pour un graphe orienté, la matrice d’adjacence est également carrée \((n \times n)\), mais c’est le coefficient \(a_{i,j}\) qui vaut \(1\) quand il y a une arête allant du sommet \(i\) au sommet \(j\).
Si on note \(A\) la matrice d’adjacence du graphe orienté ci-dessus, et \(B\) celle du graphe non orienté, on a :
\( A = \begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 1 \\ 1 & 0 & 0\end{pmatrix} \ \text{et} \ \ B = \begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix} \)
Quelques propriétés des matrices d’adjacence
- \(A\) n’est pas unique (dépend de l’ordre de numérotation des sommets)
- \(A\) est une matrice binaire
- \(A\) est symétrique si \( \mathcal{G} \) est non orienté
- \( A \) est à diagonale nulle si et seulement si \( \mathcal{G} \) est simple
- Pour un graphe simple non orienté, les degrés des sommets s’obtiennent en sommant les coefficients des lignes d’une matrice d’adjacence. Formellement : \( \forall i \in [1, n], \text{deg}(s_i) = \displaystyle \sum_{k=1}^{n} a_{i,k} \)
Notions associées aux graphes
Graphe complet : un graphe complet est un graphe non orienté dans lequel chaque paire de sommets distincts est reliée par une arête.
Graphe régulier : un graphe est dit régulier si tous ses sommets ont le même degré, c’est-à-dire qu’ils ont tous le même nombre d’arêtes.
Graphe biparti : un graphe est dit biparti si ses sommets peuvent être divisés en deux ensembles distincts de telle manière qu’il n’y a pas d’arêtes entre les sommets d’un même ensemble.
Graphe acyclique : un graphe est dit acyclique s’il ne contient pas de cycles, c’est-à-dire qu’il est impossible de revenir à un sommet en empruntant des arêtes sans repasser par un sommet déjà visité.
Ces différents types de graphes peuvent faire l’objet d’exercices ou même de questions de cours dans les sujets de concours, donc essaie d’avoir ces définitions en tête. Par ailleurs, tu peux essayer de tracer des représentations graphiques de ces graphes pour t’entraîner à les maîtriser.
Chaînes, chemins et connexité
Chaînes, chemins, cycles
Chaîne/chemin : une chaîne (si non orienté), aussi appelée chemin (si orienté) est une séquence de sommets reliés par des arêtes sans répétition de sommets. Formellement, c’est un p-uplet \((s_1, … s_p)\) dont les éléments appartiennent à \( \mathcal{S} \), qui sont consécutivement reliés par des arêtes.
La longueur d’une chaîne/chemin de \(p\) sommets vaut toujours \(p-1\) : c’est le nombre d’arêtes parcourues.
Une chaîne/chemin est “fermée” si \(s_1=s_p\).
Cycle (si orienté)/parcours (si non orienté) : un cycle/parcours est la donnée d’une chaîne fermée (si orienté)/chemin fermé (si non orienté) sans répétition d’arêtes.
Chaîne eulérienne de \( \mathcal{G} \) (graphe non orienté) : toute chaîne de \( \mathcal{G} \) passant exactement une fois par chaque arête de \( \mathcal{G} \) est appelée chaîne eulérienne.
Cycle eulérien : on appelle cycle eulérien toute chaîne eulérienne fermée. Un graphe contenant un cycle eulérien est appelé « graphe eulérien ».
Connexité
Un graphe est dit connexe s’il existe un chemin entre n’importe quel couple de sommets. On peut également parler de composantes connexes dans un graphe non orienté, qui sont les ensembles de sommets reliés entre eux mais qui ne sont pas reliés aux autres sommets du graphe.
Exemple de graphe connexe :
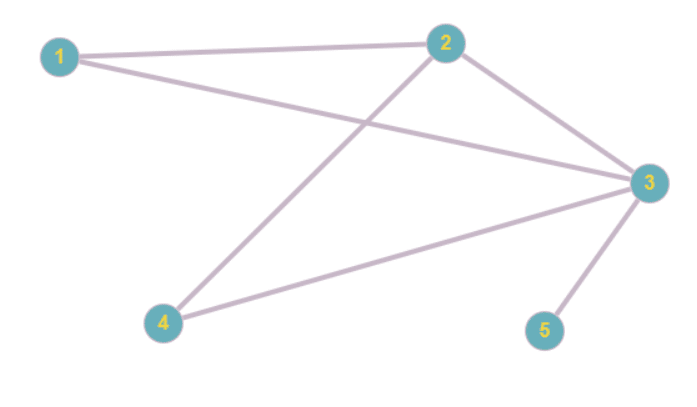
Propriétés des graphes connexes
Soit \( \mathcal{G} \)=(\( \mathcal{S} \),\( \mathcal{A} \)) un graphe connexe à \(n\) sommets, et soit \( A \) sa matrice d’adjacence.
Alors : \( \mathcal{G} \) est connexe si et seulement si la matrice \( I_n + A + A^{2} … + A^{n-1} \) est à coefficient strictement positif.
Propriétés des chaînes, chemins et cycles
Soit \( \mathcal{G} \)=(\( \mathcal{S} \),\( \mathcal{A} \)) un graphe dont la matrice d’adjacence est notée \(A\). Soit \( s \ \text{et} \ t \) deux sommets distincts.
1. Pour tout entier \(d\) strictement positif, pour tout couple d’entiers \( (i,j) \in \mathbb{N^2} \), le nombre de chaînes/chemins reliant le sommet \(s_i\) au sommet \(s_j\) vaut \(A^{d}_{i,j}\).
Soit \( \mathcal{G} \)=(\( \mathcal{S} \),\( \mathcal{A} \)) un graphe connexe dont la matrice d’adjacence est notée \(A\). Soit \( s \ \text{et} \ t \) deux sommets distincts de \( \mathcal{G} \).
2.1 : Il existe une chaîne eulérienne dans \( \mathcal{G} \) reliant les sommets \( s \ \text{et} \ t \) si et seulement si \( s \ \text{et} \ t \) sont les deux seuls sommets de degrés impairs de \( \mathcal{G} \).
2.2 : Le graphe \( \mathcal{G} \) est eulérien si et seulement si tous les sommets de \( \mathcal{G} \) sont de degrés pairs. Alors, on peut construire un cycle eulérien dans \( \mathcal{G} \) depuis n’importe quel sommet.
Réseaux sociaux
Les graphes sont souvent utilisés pour modéliser les réseaux sociaux. Cette partie du cours peut paraître enfantine, mais elle apparaît clairement dans le programme officiel. Elle nous donne des formules qui pourront être utiles lors des concours.
Soit \( \mathcal{G} \)=(\( \mathcal{S} \),\( \mathcal{A} \)) un graphe non orienté connexe.
Le degré de centralité : la centralité d’un sommet mesure son importance dans le réseau. Le degré de centralité d’un sommet \(s\) du graphe \( \mathcal{G} \) vaut \( \frac{deg(s)}{n-1} \).
Le degré d’intermédiarité : l’intermédiarité d’un sommet mesure son rôle de pont entre d’autres sommets du réseau.
Le degré d’intermédiarité d’un sommet \( v \) dans un graphe \( G \) est donné par :
\[ C(v) = \frac{2}{(n-1)(n-2)} \sum_{(s,t) \in \mathcal{S}\backslash \text{{v}}, \ s \ne t} \frac{\sigma_{st}(v)}{\sigma_{st}} \]
où :
\( \begin{align*}
& C(v) \text{ est le degré d’intermédiarité du sommet \( v \).} \\
& \sigma_{st} \text{ est le nombre total de chemins les plus courts entre les sommets \( s \) et \( t \).} \\
& \sigma_{st}(v) \text{ est le nombre de ces chemins qui passent par le sommet \( v \).} \\
& n \ \text{est le nombre total de sommets dans le graphe} \ G.
\end{align*} \)
Quelques résultats mathématiques et théorème d’Euler
Soit \( \mathcal{G} \)=(\( \mathcal{S} \),\( \mathcal{A} \)) un graphe.
Le théorème des poignées de main : dans un graphe non orienté, la somme des degrés de tous les sommets est égale au double du nombre d’arêtes. Formellement, \(\displaystyle \sum_{s \in S}deg(s) = 2Card(\mathcal{A})\).
Théorème : un graphe simple a un nombre pair de sommets de degré impair.
Théorème : un graphe acyclique d’ordre \(n\) possède au plus \(n-1\) arêtes.
Théorème : un graphe connexe d’ordre \(n\) possède au moins \(n-1\) arêtes. Ce résultat est démontrable par récurrence et constitue un bon exercice.
Lemme associé : si dans un graphe \( \mathcal{G} \), tout sommet est de degré supérieur ou égal à \(2\), alors \( \mathcal{G} \) possède au moins un cycle.
Conclusion
La théorie des graphes est un outil puissant pour l’analyse de problèmes complexes et est utilisée dans de nombreux domaines, y compris en économie, sciences sociales, informatique et optimisation. Les graphes peuvent donc naturellement donner lieu à des problèmes complexes et sont à travailler avec attention.
Tu peux également t’intéresser au fonctionnement des graphes en Python, en regardant par exemple ECRICOME 2023 (Maths Appliquées). Enfin, tu peux retrouver nos autres ressources mathématiques ici.