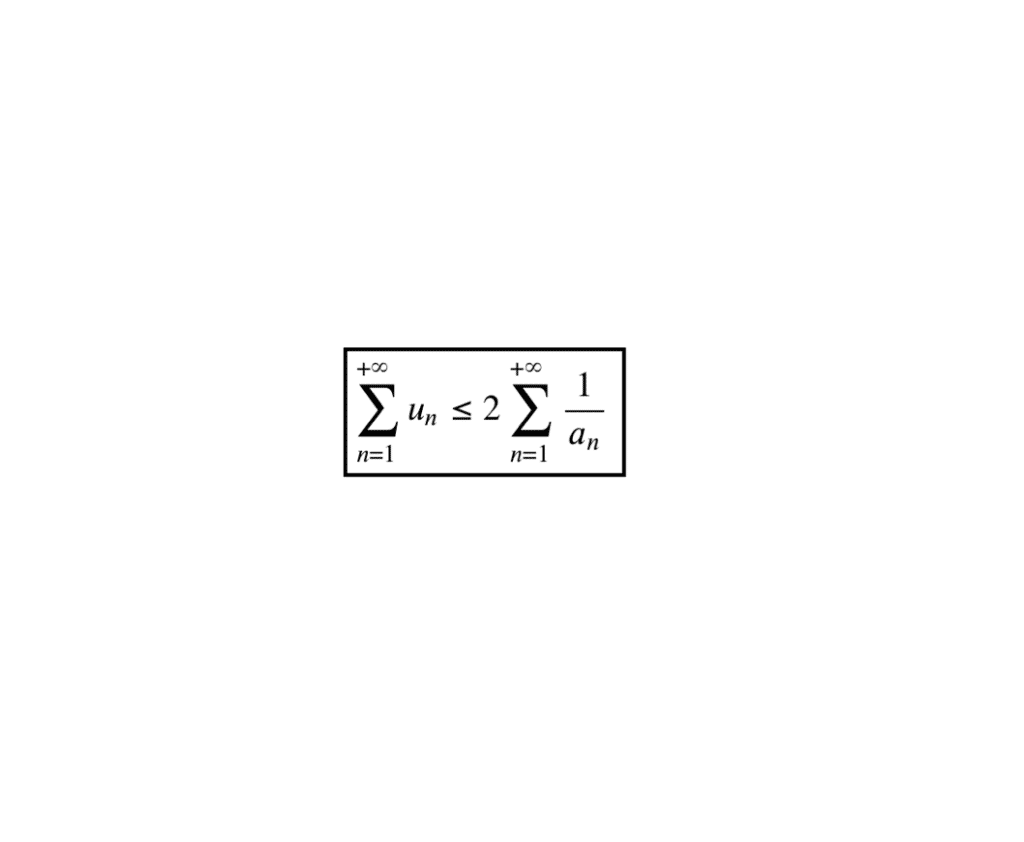On se retrouve aujourd’hui pour étudier une nouvelle notion hors programme : l’inégalité de Hardy. C’est donc l’occasion pour toi d’approfondir ta maîtrise de l’analyse, tout en ayant un coup d’avance si un exercice portant sur cette inégalité tombe aux concours.
Résultat de l’inégalité de Hardy
Il existe plusieurs formulations différentes concernant l’inégalité de Hardy mais, par souci de clarté et pour que cet article soit adapté aux préparationnaires ECG, nous allons retenir le résultat suivant :
Soit \((a_n)_{n \in \mathbb{N^*}}\) une suite de réels strictement positifs telle que la série de terme général \(\displaystyle \frac{1}{a_n}\) converge.
Alors la série de terme général \(u_n = \displaystyle \frac{n}{a_1 + a_2 + …. + a_n}\) converge également et :
\[\fbox{\(\displaystyle \sum_{n=1}^{+\infty}u_n \le 2\displaystyle \sum_{n=1}^{+\infty}\displaystyle \frac{1}{a_n}\)}\]
Un premier exemple
Pour bien comprendre ce résultat, je te propose un premier exemple en considérant la suite \((a_n)_{n \in \mathbb{N^*}},\) tel que \(\forall n \in\mathbb{N^*}, a_n = n!\).
On sait que \((a_n)_{n \in \mathbb{N^*}},\) est bien une suite de réels strictement positifs, et par définition d’une série exponentielle, \(\displaystyle\sum_{n \ge 1} a_n = \displaystyle\sum_{n \ge 1} \displaystyle\frac{1}{n!}\) converge.
Ainsi, d’après l’inégalité de Hardy, on obtient le résultat suivant :
\[\displaystyle \sum_{n=1}^{+\infty}\displaystyle\frac{n}{\left(\displaystyle \sum_{k=1}^{n}k!\right)} \le\displaystyle \sum_{n=1}^{+\infty}\displaystyle\frac{1}{n!} = \displaystyle \sum_{n=0}^{+\infty}\displaystyle\frac{1}{n!} – 1 = e – 1\]
Ce résultat se démontre assez facilement. En effet, \( \forall n \in\mathbb{N^*}, u_n = \displaystyle\frac{n}{\left(\displaystyle \sum_{k=1}^{n}k!\right)} \le \displaystyle\frac{n}{n!} = \displaystyle\frac{1}{(n – 1)!}.\)
Comme la série de terme général \(\displaystyle\frac{1}{(n – 1)!}\) converge en tant que série exponentielle, par le critère de comparaison sur les séries à termes positifs, la série de terme général \((u_n)_{n \in \mathbb{N^*}}\) converge et :
\(\displaystyle \sum_{n=1}^{+\infty}u_n \le \displaystyle \sum_{n=1}^{+\infty}\displaystyle\frac{1}{(n – 1)!} = \displaystyle \sum_{k=0}^{+\infty}\displaystyle\frac{1}{k!} = e.\)
Comme nous savons que \(2\displaystyle \sum_{n=1}^{+\infty}\displaystyle\frac{1}{a_n} = 2\displaystyle \sum_{n=1}^{+\infty}\displaystyle\frac{1}{n!} = 2(e – 1),\)et que \(e \approx 2.72,\)alors \(e\le 2(e – 1),\)
d’où :
\(\displaystyle \sum_{n=1}^{+\infty}u_n \le e \le 2\sum_{n=1}^{+\infty}\displaystyle\frac{1}{a_n} = 2(e – 1).\)
Démonstration générale de l’inégalité de Hardy
Désormais, nous allons passer à la démonstration de l’inégalité de Hardy. Si cette dernière n’est pas à connaître nécessairement par cœur, la travailler te permettra d’approfondir ta maîtrise de certains concepts importants du programme.
Considérons l’espace euclidien \(\mathbb{R}^{n}\) muni de son produit scalaire canonique, défini par : \(\forall (x, y) \in\mathbb{R}^{n}, \langle x,y\rangle = \displaystyle \sum_{i=1}^{n}x_iy_i.\)
En appliquant l’inégalité de Cauchy-Schwarz pour les vecteurs \(x = (\sqrt{a_1}, \sqrt{a_2}, …, \sqrt{a_n})\) et \(y = (\displaystyle \frac{1}{\sqrt{a_1}}, \displaystyle \frac{2}{\sqrt{a_2}}, …, \displaystyle \frac{n}{\sqrt{a_n}}),\) on obtient l’inégalité suivante :
\[\forall n \in\mathbb{N^{*}}, (1 + 2 + … + n)^2 = \displaystyle \frac{n^2(n+1)^2}{4} \le (a_1 + a_2 + … + a_n)\left( \displaystyle \frac{1}{a_1} + \displaystyle \frac{4}{a_2} + … + \displaystyle \frac{n^2}{a_n}\right)\]
Une fois cette inégalité obtenue, on peut diviser des deux côtés par \((a_1 + a_2 + … + a_n)\) qui est strictement positif, ainsi que par \(\displaystyle \frac{n^2(n + 1)^2}{4}\) qui est également strictement positif : on obtient alors l’inégalité \(\displaystyle \frac{1}{(a_1 + a_2 + … + a_n)} \le \displaystyle \frac{4}{n^2(n + 1)^2}\displaystyle \sum_{k=1}^{n}\displaystyle \frac{k^2}{a_k},\)
qui donne en multipliant de chaque côté par \(2n+1 :\)
\[\forall n \in\mathbb{N^{*}},\displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)} \le \displaystyle \frac{4(2n+1)}{n^2(n + 1)^2}\displaystyle \sum_{k=1}^{n}\displaystyle \frac{k^2}{a_k} = 4 \left(\displaystyle \frac{1}{n^2} – \displaystyle \frac{1}{(n+1)^2}\right)\displaystyle \sum_{k=1}^{n}\displaystyle \frac{k^2}{a_k}\]
Puis, en sommant cette inégalité pour \(n\) allant de \(1\)à \(N,\) on obtient :
\(\displaystyle \sum_{n=1}^{N}\displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)} \le 4\displaystyle \sum_{n=1}^{N}\left(\displaystyle \frac{1}{n^2} – \displaystyle \frac{1}{(n+1)^2}\right)\displaystyle \sum_{k=1}^{n}\displaystyle \frac{k^2}{a_k} = 4 \displaystyle \sum_{n=1}^{N}
\sum_{k=1}^{n}\displaystyle \frac{k^2}{a_k}\left(\displaystyle \frac{1}{n^2} – \displaystyle \frac{1}{(n+1)^2}\right)\)
= \(4\displaystyle \sum_{1\le k\le n \le N}\displaystyle \frac{k^2}{a_k}\left(\displaystyle \frac{1}{n^2} – \displaystyle \frac{1}{(n+1)^2}\right) = 4\sum_{k=1}^{N}\sum_{n=k}^{N}\displaystyle \frac{k^2}{a_k}\left(\displaystyle \frac{1}{n^2} – \displaystyle \frac{1}{(n+1)^2}\right)\) d’après le théorème de Fubini.
Dès lors, en simplifiant grâce à une somme télescopique, on obtient que :
\(\displaystyle \sum_{n=1}^{N}\displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)} \le 4 \sum_{k=1}^{N}\displaystyle \frac{k^2}{a_k}\left(\displaystyle \frac{1}{k^2} – \displaystyle \frac{1}{(N+1)^2}\right) = 4 \left(\sum_{k=1}^{N}\displaystyle \frac{1}{a_k}\right) – \displaystyle \left(\frac{4}{(N+1)^2}\right)\sum_{k=1}^{N}\displaystyle \frac{k^2}{a_k} \le 4\sum_{k=1}^{N}\displaystyle \frac{1}{a_k}.\)
On sait que la série de terme général \(\displaystyle \frac{1}{a_k}\) converge et est à termes positifs, d’où : \(\displaystyle \sum_{n=1}^{N}\displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)} \le 4\sum_{k=1}^{N}\displaystyle \frac{1}{a_k} \le \displaystyle \sum_{k=1}^{+\infty}\displaystyle \frac{1}{a_k}.\)
En notant \((S_N)_{N \in \mathbb{N^{*}}}\) la suite des sommes partielles de la série de terme général \(\displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)},\) on a donc la suite \((S_N)_{N \in \mathbb{N^{*}}}\) majorée. Comme cette dernière est croissante, on en déduit que la suite des sommes partielles de la série de terme général \(\displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)}\) converge, d’où la série de terme général \(\displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)}\) converge.
Enfin, comme \(\displaystyle \frac{2n}{(a_1 + a_2 + … + a_n)} \le \displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)},\)
on en déduit par critère de comparaison sur les séries à termes positifs que la série de terme général \(\displaystyle \frac{2n}{(a_1 + a_2 + … + a_n)}\) converge également, et on a alors que :
\(\displaystyle \sum_{n=1}^{N}\displaystyle \frac{2n}{(a_1 + a_2 + … + a_n)} \le \displaystyle \sum_{n=1}^{N}\displaystyle \frac{2n+1}{(a_1 + a_2 + … + a_n)} \le 4\sum_{k=1}^{N}\displaystyle \frac{1}{a_k},\) soit en passant à la limite (les séries convergeant toutes) :
\(\displaystyle \sum_{n=1}^{+\infty}\displaystyle \frac{2n}{(a_1 + a_2 + … + a_n)} \le 4\displaystyle \sum_{n=1}^{+\infty} \displaystyle \frac{1}{a_k},\) soit en divisant par 2 de chaque côté de l’inégalité :
\[\displaystyle \sum_{n=1}^{+\infty}\displaystyle \frac{n}{(a_1 + a_2 + … + a_n)} \le 2\displaystyle \sum_{n=1}^{+\infty} \displaystyle \frac{1}{a_k}\]
L’inégalité est bien prouvée.
Conclusion
L’inégalité de Hardy est déjà tombée aux concours, notamment dans l’exercice 1 de Maths EDHEC 2013 ECS.
N’hésite pas à consulter tous nos articles de mathématiques.