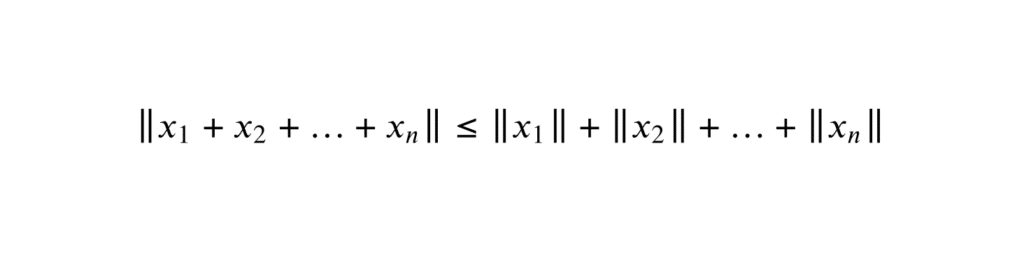L’inégalité triangulaire est un principe fondamental en géométrie et en analyse mathématique, particulièrement important pour les étudiants en classes préparatoires ECG, où elle trouve des applications variées, notamment en optimisation, en algèbre bilinéaire et en théorie des probabilités. La version généralisée de cette inégalité étend le concept au-delà des distances euclidiennes classiques, offrant un cadre plus large pour l’étude des espaces vectoriels normés.
Définition de l’inégalité triangulaire
L’inégalité triangulaire standard affirme que pour tout triplet de points \( A, B, \) et \( C \) dans un espace, la longueur du côté \( AC \) est toujours inférieure ou égale à la somme des longueurs des deux autres côtés \( AB \) et \( BC \). Mathématiquement, cela se traduit par:
\[ d(A, C) \leq d(A, B) + d(B, C) \]
où \( d \) représente la distance entre les points.
Pour généraliser cette inégalité aux espaces vectoriels normés, on considère un espace vectoriel \( V \) muni d’une norme \( \| \cdot \| \). L’inégalité triangulaire généralisée s’énonce alors comme suit:
\[ \| x + y \| \leq \| x \| + \| y \| \]
pour tous vecteurs \( x \) et \( y \) dans \( V \).
Interprétation géométrique de l’inégalité triangulaire
Géométriquement, cette inégalité signifie que dans tout espace normé, le “chemin direct” (représenté par la norme du vecteur somme) entre deux points est toujours plus court ou égal à la somme des chemins individuels. Cela est particulièrement visuel dans des espaces comme \( \mathbb{R}^2 \) ou \( \mathbb{R}^3 \), où la norme peut être envisagée comme une mesure de longueur.
Extension à la somme de n vecteurs
L’inégalité triangulaire peut être étendue à la somme de plusieurs vecteurs, ce qui est essentiel dans des contextes multidimensionnels. Cette généralisation aide à comprendre la structure des espaces vectoriels normés de dimension plus élevée et trouve des applications pratiques dans de nombreux domaines.
Formulation de l’inégalité pour n vecteurs
Supposons que nous ayons \( n \) vecteurs \( x_1, x_2, …, x_n \) dans un espace vectoriel normé \( V \). L’inégalité triangulaire généralisée pour ces \( n \) vecteurs s’énonce comme suit :
\[ \| x_1 + x_2 + \ldots + x_n \| \leq \| x_1 \| + \| x_2 \| + \ldots + \| x_n \| \]
Cette inégalité indique que la norme de la somme de \( n \) vecteurs est toujours inférieure ou égale à la somme des normes de ces vecteurs pris individuellement.
Preuve par récurrence
Pour démontrer cette inégalité, on peut utiliser le principe de récurrence :
1. Base de la récurrence : Pour \( n = 2 \), l’inégalité se réduit à la forme classique de l’inégalité triangulaire :
\[ \| x_1 + x_2 \| \leq \| x_1 \| + \| x_2 \| \]
qui est vraie par définition de la norme dans un espace vectoriel normé.
2. Hypothèse de récurrence : Supposons que l’inégalité soit vraie pour \( n \) vecteurs. C’est-à-dire :
\[ \| x_1 + x_2 + \ldots + x_n \| \leq \| x_1 \| + \| x_2 \| + \ldots + \| x_n \| \]
3. Pas de récurrence : Ajoutons un vecteur \( x_{n+1} \) et appliquons l’inégalité triangulaire à \( x_1 + x_2 + \ldots + x_n \) et \( x_{n+1} \) :
\[ \| x_1 + x_2 + \ldots + x_n + x_{n+1} \| \leq \| x_1 + x_2 + \ldots + x_n \| + \| x_{n+1} \| \]
En utilisant l’hypothèse de récurrence, nous avons :
\[ \| x_1 + x_2 + \ldots + x_n + x_{n+1} \| \leq \| x_1 \| + \| x_2 \| + \ldots + \| x_n \| + \| x_{n+1} \| \]
Ainsi, l’inégalité est prouvée pour \( n+1 \) vecteurs.
Cas d’égalité dans l’Inégalité Triangulaire Généralisée
L’analyse du cas d’égalité dans l’inégalité triangulaire généralisée offre des informations importantes sur la structure et l’orientation des vecteurs dans différents espaces normés. Ce cas particulier aide à comprendre dans quelles conditions les vecteurs se comportent de manière linéairement dépendante ou alignée, même dans des contextes multi-dimensionnels.
Pour deux vecteurs :
Considérons deux vecteurs \( x \) et \( y \) dans un espace vectoriel normé. L’inégalité triangulaire affirme que :
\[ \| x + y \| \leq \| x \| + \| y \| \]
Le cas d’égalité se produit lorsque \( x \) et \( y \) sont colinéaires et de même sens, c’est-à-dire lorsque l’un est un multiple scalaire non-négatif de l’autre. Mathématiquement, cela peut être exprimé comme \( x = \lambda y \) ou \( y = \lambda x \) pour un \( \lambda \geq 0 \). Dans ce cas, les deux vecteurs alignés ajoutent leurs magnitudes directement, rendant la somme de leurs normes égale à la norme de leur somme vectorielle.
Généralisation à n vecteurs :
Lorsqu’on généralise cette situation à \( n \) vecteurs, \( x_1, x_2, …, x_n \), l’inégalité triangulaire s’étend comme suit :
\[ \| x_1 + x_2 + \ldots + x_n \| \leq \| x_1 \| + \| x_2 \| + \ldots + \| x_n \| \]
Le cas d’égalité pour cette inégalité généralisée survient lorsque tous les vecteurs \( x_i \) sont colinéaires et orientés dans la même direction, c’est-à-dire que chaque vecteur \( x_i \) est un multiple scalaire non-négatif d’un vecteur \( x_j \) commun. Si \( x_i = \lambda_i x \) pour tous les \( i \), avec \( \lambda_i \geq 0 \) et \( x \) un vecteur fixé, alors chaque vecteur contribue linéairement à la norme totale de leur somme, réalisant ainsi l’égalité.
Cette compréhension du cas d’égalité non seulement renforce la connaissance de la structure linéaire sous-jacente des espaces vectoriels, mais aussi met en lumière les conditions spécifiques sous lesquelles les effets de superposition vectorielle sont maximisés. Ces cas sont particulièrement importants dans des applications pratiques telles que l’analyse de la stabilité des systèmes dynamiques et l’optimisation linéaire, où l’alignement des vecteurs de contrainte peut influencer significativement la solution d’un problème.
Exemple avec plusieurs vecteurs
Pour illustrer l’application de l’inégalité triangulaire généralisée à une somme de plusieurs vecteurs dans un contexte plus complexe, considérons l’espace \( \mathbb{R}^3 \) et examinons comment cette propriété peut être utilisée pour comprendre la dynamique des vecteurs dans cet espace.
Énoncé de l’exemple :
Soient \( v_1 = (1, 0, 1) \), \( v_2 = (2, 2, 0) \), \( v_3 = (0, 1, 3) \) et \( v_4 = (1, 1, 1) \) dans \( \mathbb{R}^3 \). Nous utilisons la norme euclidienne pour mesurer la longueur des vecteurs et de leur somme. Calculons la norme de la somme de ces vecteurs et comparons-la à la somme de leurs normes individuelles.
Calcul et application de l’inégalité :
1. Calcul des normes individuelles :
– \( \|v_1\| = \sqrt{1^2 + 0^2 + 1^2} = \sqrt{2} \)
– \( \|v_2\| = \sqrt{2^2 + 2^2 + 0^2} = 2\sqrt{2} \)
– \( \|v_3\| = \sqrt{0^2 + 1^2 + 3^2} = \sqrt{10} \)
– \( \|v_4\| = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3} \)
2. Calcul de la norme de la somme :
– La somme des vecteurs est \( v_1 + v_2 + v_3 + v_4 = (1+2+0+1, 0+2+1+1, 1+0+3+1) = (4, 4, 5) \)
– \( \|v_1 + v_2 + v_3 + v_4\| = \sqrt{4^2 + 4^2 + 5^2} = \sqrt{41} \)
3. Comparaison avec la somme des normes :
– Somme des normes: \( \sqrt{2} + 2\sqrt{2} + \sqrt{10} + \sqrt{3} \approx 1.41 + 2.83 + 3.16 + 1.73 = 9.13 \)
– Norme de la somme: \( \sqrt{41} \approx 6.40 \)
Conclusion sur l’inégalité triangulaire généralisée
L’inégalité triangulaire généralisée s’étend bien au-delà de ses racines géométriques, offrant une méthode puissante pour aborder des problématiques complexes dans divers domaines mathématiques tels que l’optimisation et la théorie des probabilités. En permettant l’analyse des propriétés des espaces vectoriels normés et de leurs interactions, cette généralisation de l’inégalité classique enrichit notre compréhension des structures linéaires et des dynamiques de somme de vecteurs. Ainsi, elle constitue un pilier fondamental pour résoudre des problèmes complexes dans des espaces de dimension \(n.\) Cette notion est particulièrement utile en mathématiques appliquées, en effet elle facilite le développement de stratégies efficaces pour la résolution de problèmes complexes et multidimensionnels.
Pour t’entrainer sur cette nouvelle notion tu peux réaliser les sujets mathématiques approfondies suivants :
Tu peux retrouver le méga répertoire qui contient toutes les annales de concours et leur corrigé ! Tu peux également accéder à toutes nos autres ressources mathématiques !