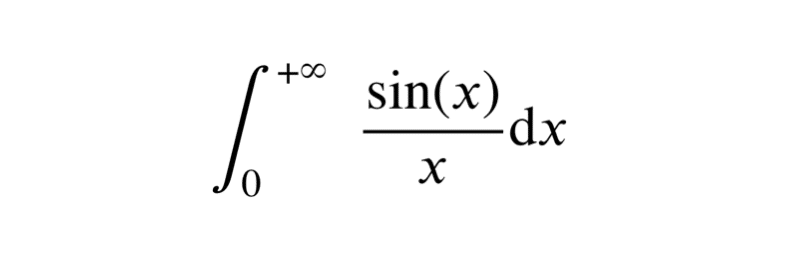L’intégrale de Dirichlet joue un rôle central dans de nombreux domaines des mathématiques, notamment en analyse et en théorie des nombres. Elle est particulièrement pertinente, car elle introduit des concepts fondamentaux de convergence et de manipulation des intégrales impropres. Des concepts qui se retrouvent fréquemment dans l’épreuve de Maths II. Cette intégrale se distingue par sa simplicité apparente et sa profondeur sous-jacente, offrant de la matière pour explorer des propriétés d’analyse. Bien que cette notion soit hors programme, sa compréhension approfondie te permettra de te préparer aux épreuves parisiennes et aux oraux de mathématiques.
Définition de l’intégrale de Dirichlet
L’intégrale de Dirichlet est définie par la relation suivante :
\[ \fbox{ \(\int_{0}^{+\infty} \frac{\sin(x)}{x} \mathrm{d}x\)} \]
Au premier abord, cette intégrale peut sembler déroutante, car elle s’étend sur un intervalle infini et le dénominateur s’annule en \(x = 0\). Cependant, elle converge vers une valeur bien définie que nous allons voir ci-dessous.
Cependant, commençons par le plus important, c’est-à-dire montrer que cette intégrale converge. Ce qui ne semble pas évident à première vue.
Démonstration de la convergence de l’intégrale de Dirichlet
Il est particulièrement important de maîtriser cette démonstration de convergence, car la première question qui te serait posée à l’écrit ou à l’oral serait de prouver que cette intégrale converge.
L’intégrale de Dirichlet est définie par l’expression \( \displaystyle \int_{0}^{+\infty} \frac{\sin(x)}{x} dx\). Pour démontrer sa convergence, il est essentiel de considérer l’intégrale sur deux intervalles distincts : de 0 à 1, et de 1 à \(+\infty\).
Sur le premier intervalle, la fonction \(\displaystyle \frac{\sin(x)}{x}\) (c’est-à-dire l’intégrande) peut être étendue par continuité en \(x = 0\) en posant sa valeur à 1, rendant ainsi la fonction continue et bornée sur cet intervalle fermé. Cette extension peut se démontrer en utilisant les développements limités. La convergence sur cet intervalle est donc garantie par le théorème de la convergence des fonctions continues sur un intervalle fermé.
Pour démontrer la convergence de l’intégrale de Dirichlet sur l’intervalle \([1,+\infty]\), nous allons introduire \(A > 1\) et nous allons procéder par intégration par parties (IPP). Cette méthode est particulièrement adaptée à notre cas, car elle permet de transformer l’intégrale initiale en une forme plus facilement analysable en termes de convergence. L’idée clé derrière l’IPP est d’exploiter la dérivée de \(\displaystyle \frac{1}{x}\) pour séparer l’intégrale en deux parties, dont l’une sera plus aisée à évaluer en termes de convergence.
Soit l’intégrale \(\displaystyle I = \int_{1}^{A} \frac{\sin(x)}{x} \mathrm{d}x\). Pour appliquer l’IPP, nous identifions les termes \(u\) et \(v\) comme suit : \( \displaystyle u = \frac{1}{x}\) dont la dérivée est \( \displaystyle -\frac{1}{x^2} \) et \(\displaystyle v^{\prime} = \sin(x) \) dont la primitive est \(v = -\cos(x)\).
Ainsi :
\( \displaystyle I = \left[-\frac{\cos(x)}{x}\right]_{1}^{A} – \int_{1}^{A} \frac{\cos(x)}{x^2} \mathrm{d}x \)
\( \displaystyle I = -\frac{\cos(A)}{A} + \frac{\cos(1)}{1} – \int_{1}^{A} \frac{\cos(x)}{x^2} \mathrm{d}x \)
Maintenant, examinons la convergence de cette expression lorsque \(A\) tend vers l’infini. Le terme \(\displaystyle -\frac{\cos(A)}{A}\) tend vers 0 quand \(A\) tend vers l’infini, car \(\cos(A)\) est borné par \([-1, 1]\) et \(\displaystyle \frac{1}{A}\) tend vers 0 (ceci se formalise à l’aide du théorème des gendarmes). Le terme \(\displaystyle \frac{\cos(1)}{1}\) est simplement une constante.
Considérons l’intégrande \(\displaystyle \frac{\cos(x)}{x^2}\) multipliée par \(x^{\frac{3}{2}}\), soit \(\displaystyle \frac{\cos(x)}{x^2} \cdot x^{\frac{3}{2}} = \frac{\cos(x)}{x^{\frac{1}{2}}}\).
D’après le théorème des gendarmes, la limite de cette expression lorsque \(x\) tend vers l’infini est : \( \displaystyle \lim_{x \to \infty} \frac{\cos(x)}{x^{\frac{1}{2}}} = 0 \). Ainsi, la convergence de \( \displaystyle \int_{1}^{A} \frac{\cos(x)}{x^2} \mathrm{d}x\) lorsque \(A\) tend vers l’infini est assurée par le critère de Riemann.
En conclusion, en faisant tendre \(A\) vers l’infini, nous voyons que chaque composant de l’expression de \(I\) converge. Ce qui démontre que l’intégrale de Dirichlet sur l’intervalle \([1, \infty)\) est convergente. Cette approche par intégration par parties non seulement confirme la convergence de l’intégrale, mais illustre aussi une technique puissante pour analyser la convergence d’intégrales impropres.
Démonstration de la valeur de l’intégrale de Dirichlet
Maintenant que nous avons établi la convergence de l’intégrale, il est intéressant de connaître sa valeur, nous avons :
\[ \fbox{\(\int_{0}^{+\infty} \frac{\sin x}{x} \mathrm{d}x = \frac{\pi}{2} \)} \]
La valeur de l’intégrale de Dirichlet \(\displaystyle \int_{0}^{+\infty} \frac{\sin(x)}{x} \mathrm{d}x\) peut être établie en utilisant une approche par décomposition en intégrales partielles sur des intervalles finis et l’utilisation de méthodes d’intégration par parties ou par des techniques de sommation de séries. Une méthode directe pour démontrer sa valeur fait souvent appel à des techniques avancées largement hors du programme d’ECG. La démonstration de ce résultat ferait l’objet d’au moins une partie d’une épreuve écrite.
Nous pouvons néanmoins proposer une piste de démonstration qui serait celle proposée dans un sujet. La méthode consiste à poser
\[ J_n = \int_{0}^{\frac{\pi}{2}} \frac{\sin((2n+1)x)}{\sin(x)} \mathrm{d}x \; \; \text{et} \; \; K_n = \int_{0}^{\frac{\pi}{2}} \frac{\sin((2n+1)x)}{x} \mathrm{d}x \]
Dans un premier temps, il faut montrer que la différence de ces deux suites tend vers 0. Ensuite, il faut montrer que la première suite est constante et égale à \(\frac{\pi}{2}\). Finalement, il faut montrer que la deuxième suite tend vers l’intégrale de Dirichlet. Il est donc possible de conclure que : \( \displaystyle \int_{0}^{+\infty} \frac{\sin x}{x} \, \mathrm{d}x = \frac{\pi}{2}. \)
Caractère semi-convergent de l’intégrale de Dirichlet
Cette intégrale est à connaître, car elle offre l’exemple d’une intégrale impropre semi-convergente. La semi-convergence, dans le contexte des intégrales, désigne une situation où une intégrale impropre converge vers une valeur finie sans pour autant converger absolument.
Cela signifie que, bien que l’intégrale de la fonction sur un intervalle donné tende vers une limite finie, l’intégrale de la valeur absolue de cette fonction sur le même intervalle diverge. En d’autres termes, la convergence de l’intégrale dépend de l’alternance des signes de la fonction et non pas uniquement de son amplitude.
Le caractère semi-convergent de l’intégrale de Dirichlet réfère au fait que bien que l’intégrale \(\displaystyle \int_{0}^{+\infty} \frac{\sin(x)}{x} \mathrm{d}x\) converge, l’intégrale de la valeur absolue \(\displaystyle \int_{0}^{+\infty} \left|\frac{\sin(x)}{x}\right| \mathrm{d}x\) diverge.
Conclusion
En somme, l’intégrale de Dirichlet, \(\displaystyle \int_{0}^{+\infty} \frac{\sin(x)}{x} \mathrm{d}x\), est un sujet fascinant qui offre un aperçu profond des concepts de convergence et de calcul intégral. Bien que son évaluation directe puisse sembler complexe en raison de l’intervalle infini et du point singulier en \(x = 0\), elle fournit un outil mathématique avec de nombreuses propriétés en analyse. Ce qui fait d’elle un candidat idéal pour les sujets de concours.
La trigonométrie expliquée dans une vidéo très complète
Si des paroles sont mieux que des mots pour ta compréhension de la trigonométrie, on t’invite à aller voir cette merveilleuse vidéo explicative de Ambroise réalisée sur notre chaîne youtube, il détaille vraiment tout sur tout de la trigonométrie dans les moindres détails…
Aller plus loin
Les fonctions de trigonométries peuvent être approfondies sous différentes formes. En effet, les fonctions sinus et cosinus ont donné lieu à de nombreuses notions hors programme (qui se trouvent régulièrement dans les sujets). Parmi elles, tu peux retrouver : voici un tableau récapitulatif de toutes nos ressources de trigonométrie sur Major Prépa, que ce soit aussi bien en termes de notions de cours comme de notions hors programme :
Tu peux retrouver ici toutes nos autres ressources mathématiques !