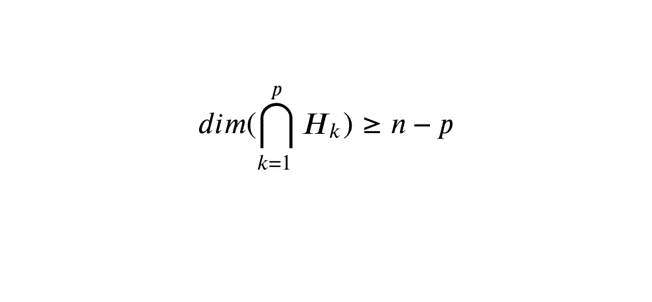Les notions hors programme sont à travailler en priorité pour les candidats visant les trois Parisiennes, bien qu’elles puissent également se retrouver dans les sujets de l’EDHEC et de l’EM Lyon, ainsi que dans les sujets d’oraux. Dans cet article, je te propose de découvrir les principales propriétés concernant la dimension d’une intersection d’hyperplans, afin de ne pas être pris(e) au dépourvu le jour J !
À savoir absolument sur les hyperplans (au programme)
Soit \(E \) un espace vectoriel de dimension finie. On appelle hyperplan de \(E\) tout sous-espace vectoriel de \(E\) de dimension égale à \(dim E-1.\)
Soit \( E \) un espace vectoriel de dimension finie. \(H\) est un hyperplan de \(E \Leftrightarrow H\) est le noyau d’une forme linéaire non nulle de \(E.\)
Ainsi, l’une des principales caractéristiques d’un hyperplan de \(E\) est sa dimension, qui vaut \(dim E -1:\) il est maintenant intéressant de se pencher sur la dimension d’une intersection de plusieurs hyperplans.
Premier cas : intersection de deux hyperplans distincts
Soit \(E\) un espace vectoriel de dimension \(n\), \(H_{1}\) et \(H_{2}\) deux hyperplans de \(E\) tels que \(H_{1} \ne H_{2}.\)
Alors :
\[\fbox{\(dim(H_{1}\cap H_{2}) = n-2 \)}\]
Démontrons ce résultat :
D’après la formule de Grassmann, \(dim (H_{1}\cap H_{2}) = dim H_{1} + dim H_{2} – dim (H_{1}+H_{2})\)
Comme \((H_{1}+H_{2}) \subset E,\) on a \(dim(H_{1}+H_{2})\le n,\)
d’où : \(dim (H_{1}\cap H_{2}) \ge dim H_{1}+ dim H_{2} – n,\)
soit \(dim(H_{1}\cap H_{2}) \ge n-2\) car \(H_{1}\) et \(H_{2}\) sont des hyperplans.
Comme par inclusion, on a \((H_{1}\cap H_{2}) \subset H_{1} \), alors \(dim(H_{1}\cap H_{2}) \le n-1.\)
Nous avons donc deux cas possibles : \(dim(H_{1}\cap H_{2}) = n-1 \) ou bien \(dim(H_{1}\cap H_{2}) = n-2. \)
Supposons que \(dim(H_{1}\cap H_{2}) = n-1 = dim H_{1} = dim H_{2}:\) comme \((H_{1}\cap H_{2}) \subset H_{1} \) et que \((H_{1}\cap H_{2}) \subset H_{2} \), il vient alors que \((H_{1}\cap H_{2}) = H_{1} = H_{2},\) ce qui est absurde, car \(H_{1} \ne H_{2}.\)
Ainsi, on obtient bien que \(dim(H_{1}\cap H_{2}) = n-2.\)
Deuxième cas : intersection de p hyperplans quelconques (inégalité)
On peut prouver par récurrence un second résultat assez intéressant sur la dimension d’une intersection de \(p\) hyperplans quelconques. Soit \(E\) un espace vectoriel de dimension \(n\) et \(H_{1}, H_{2}, …, H_{p}\) \(p\) hyperplans de \(E\), tels que \(p \in [\![1,n]\!]\). Alors, \[\fbox{\(dim (\displaystyle \bigcap_{k=1}^{p} H_{k}) \ge n-p \)}\]
Démontrons ce résultat :
Initialisation : pour \(p = 1\)
Comme \(H_{1}\) est bien un hyperplan, sa dimension vaut bien \(n-1\). Le cas \(p=1\) est donc vrai.
Hérédité :
Supposons qu’il existe \(p\in [\![1,n-1]\!]\), tel que \(dim (\displaystyle \bigcap_{k=1}^{p} H_{k}) \ge n-p.\)
Montrons alors que \(dim (\displaystyle \bigcap_{k=1}^{p+1} H_{k}) \ge n-(p+1) \)
On sait d’après la relation de Grassmann que :
\(dim (\displaystyle \bigcap_{k=1}^{p+1} H_{k}) = dim ((\displaystyle \bigcap_{k=1}^{p} H_{k}) \cap H_{p+1} ) = dim (\displaystyle \bigcap_{k=1}^{p} H_{k}) + dim ( H_{p+1}) – dim ((\displaystyle \bigcap_{k=1}^{p} H_{k}) + H_{p+1})\)
= \((n-p) + (n-1) – dim ((\displaystyle \bigcap_{k=1}^{p} H_{k}) + H_{p+1})\) par hypothèse de récurrence et car \(H_{p+1}\) est un hyperplan de \(E\).
Or, comme \(((\displaystyle \bigcap_{k=1}^{p} H_{k}) + H_{p+1}) \subset E \), on obtient que \(dim ((\displaystyle \bigcap_{k=1}^{p} H_{k}) + H_{p+1}) \le dim E = n,\)
d’où : \(dim (\displaystyle \bigcap_{k=1}^{p+1} H_{k}) \ge (n-p) + (n-1) -n = n- (p+1) \), ce qui achève donc l’hérédité.
Finalement, l’inégalité est bien prouvée par récurrence.
Troisième cas : intersection de p hyperplans quelconques (égalité)
Le résultat prouvé précédemment est intéressant, car il n’y a pas de conditions sur les hyperplans choisis. Maintenant, comme on sait d’après le cours que tout hyperplan est défini comme le noyau d’une forme linéaire non nulle, on peut obtenir un résultat encore plus intéressant en rajoutant une condition sur les formes linéaires non nulles associées à nos hyperplans.
Soit \(E\) un espace vectoriel de dimension finie, \(p\in [\![1,n]\!].\) En choisissant alors \(p\) hyperplans \(H_{1}, H_{2},…, H_{p}\) définis par \(p\) formes linéaires non nulles et linéairement indépendantes \((f_1, f_2,…, f_p)\), c’est-à-dire tels que la famille \((f_1, f_2,…, f_p)\) de \(\mathcal{L}(E,\mathbb{R})\) soit libre, alors :
\[\fbox{\(dim (\displaystyle \bigcap_{k=1}^{p} H_{k}) = n-p \)}\]
Démonstration :
Je ne vais pas détailler ici l’entièreté de la démonstration, car cela peut être l’objet de toute une partie d’un problème, comme ce fut notamment le cas dans l’épreuve Maths EM Lyon 2023 Appro . Toutefois, certaines idées peuvent être retenues :
Nous allons poser \(f\) une application linéaire de \(E\) dans \(\mathbb{R}^{p}\), tel que \(\forall x \in E, f(x)=(f_k (x))_{1 \le k \le
p}.\)
En montrant que \(rg(f)=p,\) (ce qui se démontre plus longuement, notamment dans le problème de Maths EM Lyon 2023 Appro), et en prouvant que \(\text{Ker}(f)=\displaystyle\bigcap_{k=1}^{n} \text{Ker}(f_k)\), on obtient finalement que :
\(dim(\displaystyle\bigcap_{k=1}^{n} \text{Ker}(f_k) = dim (\text{Ker}(f)) = dim E – rg(f) = n-p,\) et cela par le théorème du rang.
N’hésite pas à consulter tous nos articles de mathématiques !