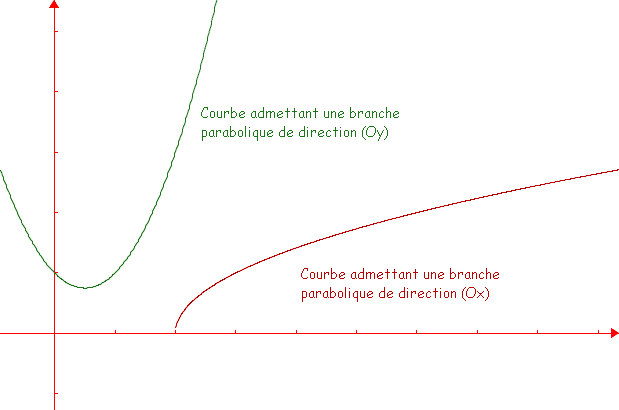Il arrive que certains sujets demandent aux candidats de représenter graphiquement une fonction. En plus de tracer l’allure de la courbe et d’éventuels points d’inflexion, ce type de question demande également (implicitement ou explicitement) de représenter les éventuelles asymptotes et branches infinies de la fonction en question. En effet, si tu ne le fais pas, le correcteur considérera que tu n’auras traité que partiellement la question !
Dans cet article, tu trouveras les rappels de cours adéquats qui te permettront de déterminer si ta fonction admet une asymptote et/ou une branche infinie, mais aussi de déterminer l’équation de la branche infinie si elle existe !
Dans tout ce qui suit, on notera \( C_f \) la courbe représentative d’une fonction \(f\).
Cas n° 1 : les asymptotes verticales
Si \( \lim \limits_{x \ \to \ x_0} f(x) = ± \infty \), alors \(C_f\) admet une asymptote verticale d’équation \( x = x_0 \)
Cas n° 2 : les asymptotes horizontales
Soit \(l \in \mathbb{R}\).
Si \(\lim \limits_{x \to +\infty} f(x) = l\), alors \(C_f\) admet une asymptote horizontale d’équation \( y = l \)

Cas n° 3 : les branches paraboliques
Pour admettre une branche parabolique, il faut que \( \lim \limits_{x \to +\infty} f(x) = ± \infty \)
Plusieurs sous-cas se présentent alors :
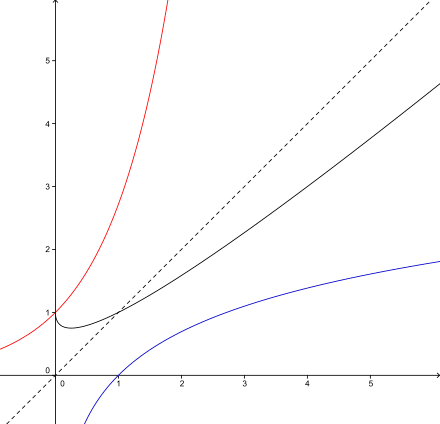
- si \( \displaystyle \lim \limits_{x \to +\infty} \frac {f(x)}{x} = ± \infty \), alors \(C_f\) admet en \(+\infty\) une branche parabolique en direction de l’axe des ordonnées (courbe rouge sur le schéma ci-dessous) ;
- si \( \displaystyle \lim \limits_{x \to +\infty} \frac {f(x)}{x} = 0 \), alors \(C_f\) admet en \(+\infty\) une branche parabolique en direction de l’axe des abscisses (courbe bleue sur le schéma ci-dessous).
Cas n° 4 : les asymptotes obliques
Pour admettre une asymptote oblique, il faut que \( \lim \limits_{x \to +\infty} f(x) = ± \infty \)
À nouveau, plusieurs sous-cas se présentent :
- si \( \displaystyle \lim \limits_{x \to +\infty} \frac {f(x)}{x} = a \ (a \in \mathbb{R^{*}})\), et si \( \lim \limits_{x \to +\infty} (f(x) \ – ax) = ± \infty \), alors \(C_f\) admet en \(+\infty\) une asymptote oblique d’équation \(y=ax\)
- si \( \displaystyle \lim \limits_{x \to +\infty} \frac {f(x)}{x} = a \ (a \in \mathbb{R^{*}})\), et si \( \lim \limits_{x \to +\infty} (f(x) \ – ax) = b \ (b \in \mathbb{R^{*}}) \), alors \(C_f\) admet en \(+\infty\) une asymptote oblique d’équation \(y=ax+b\)
Quelques remarques
- On a bien entendu des théorèmes équivalents en \( -\infty\)
- \( y = ax+b\) est une asymptote oblique de \(f\) en \(± \infty \Leftrightarrow \lim \limits_{x \to +\infty} (f(x) \ – ax+b) = 0\). Il s’agit d’une propriété au programme, n’hésite donc surtout pas à l’utiliser. Elle te permettra en plus de te démarquer des autres candidats.
Quelques annales
Les annales suivantes demandent de tracer les allures des courbes :
- Ecricome 2004 – Exercice 2
- EML 2014 – Problème 1
- EML 2005 – Problème 2
- EML 2010 – Problème 2
- Maths II 2015
N’hésite pas à aller consulter nos autres ressources mathématiques !