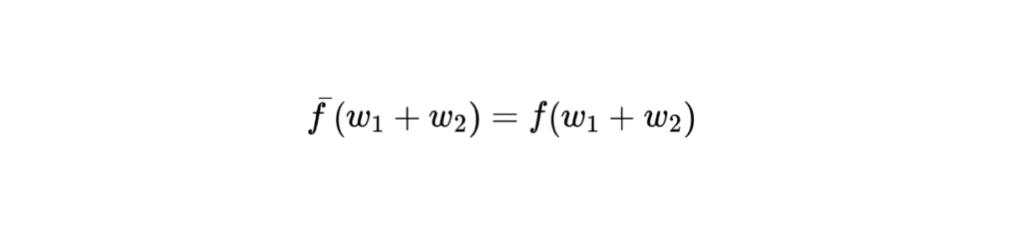En algèbre linéaire, l’étude des endomorphismes est fondamentale pour comprendre les structures des espaces vectoriels et leurs transformations. Parmi les endomorphismes, les endomorphismes induits occupent une place particulière. Ces endomorphismes sont obtenus à partir de la restriction ou de la projection d’un espace vectoriel sur un sous-espace vectoriel. Cet article explore en détail la notion d’endomorphisme induit, ses propriétés, et ses applications principales. Bien que cette notion soit hors programme il est courant de la retrouver aux écrits et aux oraux de mathématiques.
Définition de l’Endomorphisme Induit
Considérons un espace vectoriel \( V \) sur le corps \( \mathbb{R} \) et un sous-espace vectoriel \( W \subseteq V \). Si \( f: V \to V \) est un endomorphisme, nous pouvons définir un endomorphisme induit \( \bar{f}: W \to W \) par restriction de \( f \) à \( W \). Plus formellement, l’endomorphisme induit \( \bar{f} \) est défini par :
\[ \bar{f}(w) = f(w) \quad \text{pour tout } w \in W \]
Propriétés de l’Endomorphisme Induit
Les propriétés de l’endomorphisme \( f \) se reflètent généralement dans l’endomorphisme induit \( \bar{f} \). Par exemple, si \( f \) est un endomorphisme linéaire, alors \( \bar{f} \) sera également linéaire. En particulier, pour \( w_1, w_2 \in W \) et \( \lambda \in \mathbb{R} \), nous avons :
\[ \bar{f}(w_1 + w_2) = f(w_1 + w_2) = f(w_1) + f(w_2) = \bar{f}(w_1) + \bar{f}(w_2) \]
\[ \bar{f}(\lambda w_1) = f(\lambda w_1) = \lambda f(w_1) = \lambda \bar{f}(w_1) \]
Exemple d’Endomorphisme Induit
Considérons l’espace vectoriel \( \mathbb{R}^3 \) et le sous-espace \( W \) défini par le plan \( x + y + z = 0 \). Supposons que \( f: \mathbb{R}^3 \to \mathbb{R}^3 \) soit défini par :
\[ f(x, y, z) = (2x – y, 2y – z, 2z – x) \]
Nous pouvons restreindre \( f \) au sous-espace \( W \). Si \( (x, y, z) \in W \), alors \( x + y + z = 0 \), et l’endomorphisme induit \( \bar{f} \) sera donné par :
\[ \bar{f}(x, y, z) = f(x, y, -x – y) = (2x – y, 2y – (-x-y) , 2(-x – y) -x)\]
Il est essentiel de vérifier que \( \bar{f}(x, y, -x – y) \in W \) pour tout \( (x, y, z) \in W \). En effet, :
\[ \bar{f}(x, y, z) = (2x – y, 3y + x, -3x-2y ) \]
et :
\[ (2x – y) + (3y + x) + (-3x -2y) = 0 \]
Ce qui confirme que \( \bar{f} \) est bien une application de \( W \) dans \( W \).
Endomorphismes Induits par des Projections
Une autre manière de comprendre les endomorphismes induits est à travers les projections. Supposons que \( V \) soit un espace vectoriel sur \( \mathbb{R} \) et que \( V = W \oplus W’ \) soit une décomposition directe en deux sous-espaces \( W \) et \( W’ \). La projection \( P \) de \( V \) sur \( W \) parallèlement à \( W’ \) est un endomorphisme \( P: V \to V \) tel que \( P(v) = w \) pour tout \( v = w + w’ \) avec \( w \in W \) et \( w’ \in W’ \). L’endomorphisme induit par \( P \) sur \( W \) est simplement l’identité sur \( W \), c’est-à-dire :
\[ \bar{P}(w) = w \quad \text{pour tout } w \in W \]
Les projections jouent un rôle clé dans de nombreuses applications, notamment dans la résolution de systèmes d’équations linéaires où elles permettent d’isoler et de traiter des sous-espaces de manière indépendante.
Endomorphismes Induits et Diagonalisation
Un aspect important des endomorphismes induits est leur comportement vis-à-vis de la diagonalisation. Supposons que \( f: V \to V \) soit un endomorphisme diagonalisable, c’est-à-dire qu’il existe une base de \( V \) composée de vecteurs propres de \( f \). Si \( W \subseteq V \) est un sous-espace stable par \( f \), c’est-à-dire \( f(W) \subseteq W \), alors \( \bar{f}: W \to W \) peut hériter de la diagonalisation de \( f \). En d’autres termes, il existe une base de \( W \) composée de vecteurs propres de \( \bar{f} \) qui sont aussi des vecteurs propres de \( f \).
Endomorphismes Induits et Formes Bilinéaires
Les endomorphismes induits sont également pertinents dans l’étude des formes bilinéaires. Supposons que \( V \) soit un espace vectoriel muni d’une forme bilinéaire \( B: V \times V \to \mathbb{R} \). Si \( f: V \to V \) est un endomorphisme qui préserve \( B \), c’est-à-dire \( B(f(u), f(v)) = B(u, v) \) pour tous \( u, v \in V \), alors l’endomorphisme induit \( \bar{f}: W \to W \) sur un sous-espace \( W \subseteq V \) préserve également la restriction de \( B \) à \( W \). Cette propriété est utile dans l’étude des espaces euclidiens et hermitiens, où les formes bilinéaires symétriques ou hermitiennes jouent un rôle crucial.
Endomorphismes Induits et Polynômes de Matrices
Un autre domaine où les endomorphismes induits apparaissent naturellement est l’étude des polynômes de matrices. Si \( A \) est une matrice représentant un endomorphisme \( f: V \to V \) et \( W \subseteq V \) est un sous-espace stable par \( f \), alors l’endomorphisme induit \( \bar{f}: W \to W \) est représenté par une sous-matrice de \( A \). Les polynômes en \( A \), tels que le polynôme caractéristique ou le polynôme minimal, se restreignent alors à des polynômes en la sous-matrice représentant \( \bar{f} \).
Propriétés Spectrales des Endomorphismes Induits
Une question intéressante concerne les propriétés spectrales des endomorphismes induits. En particulier, si \( \lambda \) est une valeur propre de \( f \) avec un vecteur propre associé \( v \), et si \( v \in W \), alors \( \lambda \) est également une valeur propre de \( \bar{f} \) avec le même vecteur propre \( v \). Cependant, l’ensemble des valeurs propres de \( \bar{f} \) peut être strictement inclus dans celui de \( f \).
Considérons par exemple \( f: \mathbb{R}^3 \to \mathbb{R}^3 \) défini par :
\[ f(x, y, z) = (2x, 3y, z) \]
et \( W \subset \mathbb{R}^3 \) le sous-espace \( z = 0 \). L’endomorphisme induit \( \bar{f}: W \to W \) est alors donné par :
\[ \bar{f}(x, y) = (2x, 3y) \]
Les valeurs propres de \( f \) sont \( 2, 3,0 \) et \( 1 \), tandis que les valeurs propres de \( \bar{f} \) sont \( 2 \) et \( 3 \).
Conclusion
Les endomorphismes induits offrent un outil puissant pour l’analyse des sous-espaces vectoriels et de leurs transformations. En restreignant ou en projetant des endomorphismes, nous obtenons de nouvelles applications linéaires qui conservent des propriétés importantes tout en simplifiant parfois l’étude de structures complexes. Cette notion est particulièrement utile en algèbre linéaire et dans divers domaines des mathématiques avancées, offrant une perspective enrichissante sur la manière dont les espaces vectoriels peuvent être manipulés et compris. Ainsi bien que cette notion soit hors programme, t’entraîner à manipuler ces endomorphismes te permettra de te préparer aux épreuves parisiennes et plus particulièrement au Maths I qui fait régulièrement apparaitre cette notion.
Pour t’entraîner sur cette notion tu peux réaliser les sujets suivants :
Tu peux retrouver ici toutes nos autres ressources mathématiques !