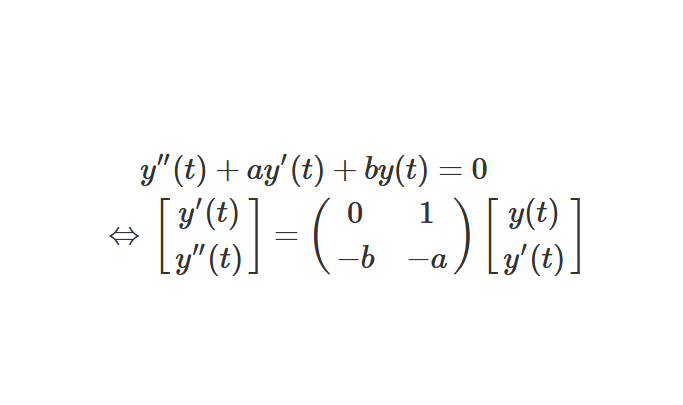Les équations différentielles, tout comme les systèmes différentiels, font leur entrée au programme d’ECG Maths Appliquées. Il existe plusieurs liens entre ces objets et il est important que tu les aies tous en tête afin d’avoir une vision claire de la chose.
Définition et théorèmes
Soit \( n \in \mathbb{N} \)
Ce qu’il faut déjà bien comprendre, c’est que lorsque l’on parle de système différentiel, on parle d’une matrice de fonctions. On peut définir \(X\) une application d’un intervalle \(I\) de \(\mathbb{R} \) à valeur dans \( \mathcal{M}_{n,1}(\mathbb{R}) \) qui intègre \(n\) fonctions composantes (\(x_1, x_2… x_n) \) telles que :
\[\forall t \in I, X(t) =\begin{bmatrix}x_1(t) \\ x_2(t) \\\vdots \\x_n(t)\end{bmatrix}\]
Et si (\(x_1, x_2… x_n) \) sont dérivables sur \(I\), alors :
\[\forall t \in I, X'(t) =\begin{bmatrix}x’_1(t) \\ x’_2(t) \\\vdots \\x’_n(t)\end{bmatrix}\]
Théorème : Soit \(B \in \mathcal{M}_{n}(\mathbb{R}) \). On suppose encore les \(n\) composantes de \(X\) dérivables sur \(I\). Alors, les composantes de \(BX\) sont dérivables sur \(I\) et \((BX)’ = BX’ \).
Théorème : Soit \(Y\) une application de \(I\) dans \( \mathcal{M}_{n,1}(\mathbb{R}) \), \(g\) une fonction dérivable de \(I\) dans \( \mathbb{R} \) et \(V \in \mathcal{M}_{n,1}(\mathbb{R}) \).
Si on a \(Y(t) = g(t)V\), alors les \(n\) composantes de \(Y\) sont dérivables et \(Y'(t) = g'(t)V \).
Voilà, les bases sont posées pour pouvoir étudier sereinement les ponts que la théorie trace entre équations différentielles et systèmes linéaires.
Réécritures des équations différentielles en systèmes différentiels
Considérons \(I\), un intervalle non vide de \(\mathbb{R}\).
Soit \((E)\) une équation différentielle linéaire homogène du deuxième ordre avec coefficients constants sur \(I\), exprimée sous forme normalisée :
\( \begin{align}
(E) : y^{\prime \prime} + ay’ + by = 0, \quad \text{d’inconnue } y \in \mathcal{A}(I, \mathbb{R})
\end{align} \)
Nous définissons la matrice \(A\) comme suit :
\[A =\begin{pmatrix}0 & 1 \\-b & -a\end{pmatrix} \]
En utilisant cette matrice, nous pouvons réécrire l’équation \((E)\) sous forme de système différentiel : \( \begin{align}
(S) : X’ = AX,
\end{align} \)
où \(X\) est une fonction inconnue définie sur \(I\) et à valeurs dans l’espace des matrices \(M_{2,1}(\mathbb{R})\).
Pour toute fonction \(y\) appartenant à \(A(I, \mathbb{R})\), nous définissons le vecteur colonne \(Y(t)\) comme suit, pour tout \(t\) dans \(I\) :\[Y(t) =\begin{pmatrix}y(t) \\y'(t)\end{pmatrix}.\]
Nous montrons que les deux affirmations suivantes sont équivalentes :
\( \begin{align}
\text{(i)} & \quad y \text{ est une solution de } (E); \\
\text{(ii)} & \quad Y \text{ est une solution de } (S).
\end{align} \)
Démonstration
Je vais ici te démontrer cette équivalence, car il est absolument nécessaire que tu saches parfaitement passer de l’un à l’autre de manière fluide, sans forcément devoir utiliser ce théorème comme une boîte noire. Je reprends les notations introduites plus haut.
Supposons que \(y\) est solution de \(E\). On a l’équivalence :
\( \begin{align*}
\forall t \in I, \ & y^{\prime \prime}(t) + ay'(t) +by(t) = 0 \\
\Leftrightarrow & \ y^{\prime \prime}(t) = -ay'(t) -by(t) \\
\Leftrightarrow & \ \begin{bmatrix}y'(t) \\ y^{\prime \prime}(t) \end{bmatrix} = \begin{pmatrix} 0 & 1 \\ -b & -a\end{pmatrix} \begin{bmatrix}y(t) \\ y'(t) \end{bmatrix}
\end{align*} \)
De fait, si tu développes le produit matriciel de droite, tu verras que l’on retombe bien sur l’équation différentielle citée au-dessus, accompagnée d’une égalité « inutile » donnant \(y'(t) = y'(t) \).
Généralisons ce résultat à \(n\) composantes.
Soit \(n \in \mathbb{N}^*\).
Soit \((E)\) une équation différentielle linéaire homogène d’ordre \(n\) à coefficients constants sur \(I\), écrite sous forme normalisée.
Alors, il existe \(n\) réels \(a_0, a_1, \ldots, a_{n-1}\) tels que \((E)\) se présente de la manière suivante : \[(E) : y^{(n)} + \sum_{k=0}^{n-1} a_k y^{(k)} = 0 \quad \text{d’inconnue } y \in A(I, \mathbb{R})\]
On pose :
\[A = \begin{pmatrix}
0 & 1 & 0 & \ldots & 0 \\
0 & 0 & 1 & \ldots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \ldots & 1 \\
-a_0 & -a_1 & -a_2 & \ldots & -a_{n-1}
\end{pmatrix}.\]
On note \((S)\) le système différentiel :
\[(S) : X’ = AX \quad \text{d’inconnue } X \in A(I, M_{n,1}(\mathbb{R})).\]
Soit \(y \in A(I, \mathbb{R})\).
On pose, pour tout \(t \in I\),
\[Y(t) = \begin{pmatrix}
y(t) \\
y'(t) \\
\vdots \\
y^{(n-1)}(t)
\end{pmatrix}.\]
Alors, les deux assertions suivantes sont équivalentes :
\( \begin{align}
(i) & \quad y \text{ est solution de } (E); \\
(ii) & \quad Y \text{ est solution de } (S).
\end{align} \)
Exemple
Si l’on prend \( (E) : y^{\prime \prime} + 5y’ – 2y = 0, \quad \text{d’inconnue } y \in \mathcal{A}(I, \mathbb{R}) \)
Alors, en posant \( A =\begin{pmatrix}0 & 1 \\2 & -5\end{pmatrix}, \ Y = \begin{pmatrix}y(t) \\y'(t)\end{pmatrix} \) et \( (S) : X’ = AX \)
Alors, les deux assertions suivantes sont équivalentes :
\( \begin{align}
(i) & \quad y \text{ est solution de } (E); \\
(ii) & \quad Y \text{ est solution de } (S).
\end{align} \)
Mais tu dois également être capable d’adapter la méthode précédente à des systèmes intégrant des équations différentielles, que tu vas devoir transformer en égalité matricielle.
Donnons-nous le système d’équations différentielles donné par :
\[
(S) : \forall t \in \mathbb{R},
\begin{cases}
x’_1(t) &= -x_1(t) + 4x_2(t) + 2x_3(t) \\
x’_2(t) &= -x_1(t) + 2x_2(t) + x_3(t) \\
x’_3(t) &= \phantom{-x_1(t) +.}2x_2(t) + x_3(t)
\end{cases}
\]
avec les inconnues \((x_1, x_2, x_3) \) qui sont des fonctions dérivables de \( \mathbb{R} \ dans \ \mathbb{R}\)
Alors, tu vois qu’on peut très simplement réécrire \((S)\) sous forme matricielle ainsi :
\[ (S) : X’=AX \]
où : \( Y = \begin{pmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \end{pmatrix} \text{et} \ A=\begin{pmatrix} -1 & 4 & 2\\ -1 & 2 & 1 \\ 0 & 2 & 1\end{pmatrix} \)
Alors, les deux assertions suivantes sont équivalentes :
\( \begin{align}
(i) & \quad (x_1, x_2, x_3) \ \text{ est solution de } (E); \\
(ii) & \quad Y \text{ est solution de } (S).
\end{align} \)
Le mécanisme de démonstration est exactement le même que pour le cas particulier précédent. Un bon exercice consiste à essayer de mimer la preuve précédente pour arriver à démontrer ce résultat. Encore une fois, comprendre ce mécanisme de passage te permettra d’aborder sereinement la prochaine partie, qui pourrait bien être la plus importante.
Réduction des systèmes différentiels
Cette méthode est déjà vue comme un classique des sujets de concours (en particulier EDHEC/EM, et elle sera probablement poussée dans les Parisiennes). Voici une idée générale de la façon dont tu peux procéder.
Soit \(I\) un intervalle non vide de \(\mathbb{R}\), non réduit à un point.
Considérons un entier \(n \in \mathbb{N}^*\) et une matrice \(A \in M_n(\mathbb{R})\).
Réduire la matrice \(A\), c’est trouver une matrice carrée simple \(B\) d’ordre \(n\) et une matrice carrée inversible \(P\) d’ordre \(n\) telles que \(A = PBP^{-1}\).
Nous souhaitons résoudre le système linéaire différentiel :
\[(SA) : X’ = AX \quad \text{d’inconnue } X \in A(I, M_{n,1}(\mathbb{R})).\]
Pour cela, nous nous servirons de la résolution du système différentiel auxiliaire :
\[(SB) : Y’ = BY \quad \text{d’inconnue } Y \in A(I, M_{n,1}(\mathbb{R})).\]
Le système \((SB)\) est généralement plus simple à résoudre que \((SA)\), car la matrice \(B\) possède plus de coefficients nuls que \(A\). Idéalement, \(B\) serait une matrice diagonale, ce qui rendrait les \(n\) équations différentielles linéaires du système \((SB)\) aisées à résoudre, étant indépendantes les unes des autres.
Il faut donc établir un lien clair entre les solutions de \((SA)\) et celles de \((SB)\). Le voici.
On reprend les notations précédentes, avec \((A,B)\) deux matrices de \( \mathcal{M}_{n}(\mathbb{R}) \), et \(P\) une matrice inversible de \( \mathcal{M}_{n}(\mathbb{R}) \) telles que \( A = PBP^{-1} \).
Soit \( X \in \mathcal{A}(I, \mathbb{R}) \). On reprend \((SA)\) et \((SB)\), et on peut alors dire que :
\[ X \ \text{est solution de} \ (SA) \ \text{si et seulement si} \ P^{-1}X \ \text{est solution de} \ (SB) \]
La démonstration de ce théorème est très simple, mais tu devras la refaire à chaque utilisation du théorème. C’est pourquoi je te le démontre ici. On reprend les mêmes notations.
Supposons \(X\) solution de \((SA)\). On a l’équivalence :
\( \begin{align*}
& \phantom{\Leftrightarrow – } X’ = AX \\
& \Leftrightarrow X’ = PBP^{-1}X \\
& \Leftrightarrow P^{-1}X’ = BP^{-1}X \\
& \Leftrightarrow (P^{-1}X)’ = BP^{-1}X, \ \text{rappelle-toi du premier théorème !} \\
& \Leftrightarrow Y’ = BY, \ \text{avec} \ Y = P^{-1}X
\end{align*} \)
Exemple
Prenons ici l’exemple du sujet EMLYON 2023 (Maths Appliquées). On s’intéresse au III de l’exercice 2.
On nous donne \( B = \begin{pmatrix} -1 & -4 \\ 1 & 3\end{pmatrix} \). On trouve que \(B\) n’est pas diagonalisable, mais on trouve une matrice \(Q = \begin{pmatrix} 2 & -1 \\ -1 & 0\end{pmatrix} \) et une matrice triangulaire \(T = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \) telles que \( B = TQT^{-1} \).
Résolvons alors sur \( \mathbb{R} \) le système différentiel suivant :
\[
\begin{cases}
x’ = -x – 4y \\
y’ = x + 3y
\end{cases}
\]
On voit qu’en posant \( X =\begin{bmatrix} x \\ y \end{bmatrix} \) avec \((x,y) \) deux fonctions dérivables sur \( \mathbb{R} \), ce système équivaut au système \( (S_1) : X’=BX \)
On va également se servir du système \( (S_2) : Y’ = TY \), et le lien nous donne que \(X\) est solution de \((S_1) \) si et seulement si \(Q^{-1}X\) est solution de \((S_2) \).
On pose \(Y= \begin{bmatrix} a \\ b \end{bmatrix} \) avec \((a,b) \) deux fonctions dérivables sur \( \mathbb{R} \) et \((S_2) \) donne \begin{cases}a’ = a + b \\ b’ = b\end{cases}
On voit donc que \(b\) est de la forme « exponentielle multipliée par constante », puis on résout la première équation à l’aide de méthodes classiques (voir cet article).
On trouve des fonctions de la forme :
\( \forall t \in \mathbb{R}, b(t) = C_2e^{t}, C_2 \in \mathbb{R} \\
\forall t \in \mathbb{R}, a(t) = C_1e^{t} + C_2te^{t}, (C_1,C_2) \in \mathbb{R^2} \)
Pour finalement trouver la solution, il ne reste plus qu’à multiplier par \(Q\) à gauche, puisque :
Pour tout \( t \in \mathbb{R} \), \( X(t) = QY(t) \) (1). Donc :
\[
\forall t \in \mathbb{R}, \ X(t) =
\begin{bmatrix}
2C_1e^t + 2C_2te^t – C_2e^t \\
-C_1e^t – C_2te^t
\end{bmatrix}, (C_1, C_2) \in \mathbb{R}^2
\]
(1) De fait, la solution \(Y\) que l’on avait alors était égale à \(Q^{-1}X\), ce qui explique que pour trouver \(X\), on multiplie finalement la matrice \( Y= \begin{bmatrix} a \\ b \end{bmatrix}\) par la matrice \(Q\) à gauche.
Conclusion
Ces liens entre équations différentielles et systèmes différentiels sont importants et retomberont à coup sûr dans les sujets des prochaines années. Tu dois donc bien comprendre ces liens pour pouvoir les manipuler avec aisance aux concours.
Tu peux également retrouver toutes nos autres ressources mathématiques ici.