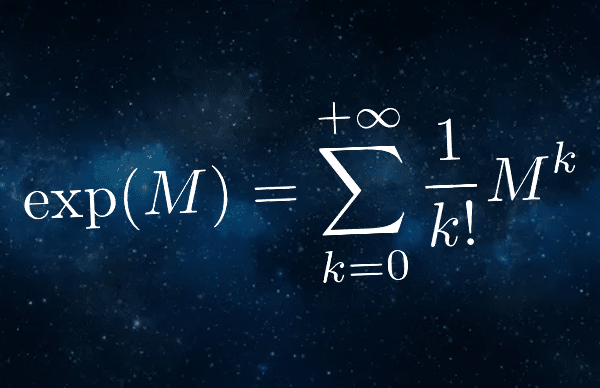Les notions hors programme sont à travailler en priorité par les candidats visant les trois Parisiennes. Cet article te propose de découvrir les limites et les exponentielles de matrices, déjà apparues dans plusieurs sujets de concours, pour mieux t’aider à les comprendre si tu te trouves face à ce sujet un jour de concours. Il te permettra aussi de faire le lien avec la notion de densité d’un ensemble.
Avant d’expliquer les exponentielles de matrice, il convient d’introduire la notion de limites de matrices pour mieux comprendre la notion hors programme.
Limites de matrices
On fixe un entier \(p\in\mathbb N^*\).
Rappels
Le produit scalaire canonique sur \(\mathcal M_p(\mathbb R)\), également appelé produit scalaire de Frobenius, est défini par
\[\forall A,B\in\mathcal M_p(\mathbb R), \quad \langle A,B\rangle = \text{Tr}({}^tAB)\]
De plus, si l’on note \(A=(a_{i,j})\) et \(B=(b_{i,j})\), on a : \(\langle A,B\rangle =\displaystyle \sum_{i=1}^p\sum_{j=1}^p a_{i,j}b_{i,j}\).
On peut alors définir la norme sur \(\mathcal M_p(\mathbb R)\) associée à ce produit scalaire :
\[\forall A\in\mathcal M_p(\mathbb R), \quad \|A\| = \sqrt{\text{Tr}({}^tAA)} = \displaystyle \sqrt{\sum_{i=1}^p\sum_{j=1}^p a_{i,j}^2}\]
Attention : parfois le sujet peut introduire une autre norme sur \(\mathcal M_p(\mathbb R)\). Par exemple, si l’on note \(A=(a_{i,j})\), les formules \(\|A\|_\infty=\max_{1\leq i,j\leq p}|a_{i,j}|\), ou encore \(\|A\|_1=\sum_{i=1}^p\sum_{j=1}^p |a_{i,j}|\) définissent deux autres normes sur \(\mathcal M_p(\mathbb R)\).
Pour cet article, nous prendrons la norme de Frobenius. Mais un jour de concours, il faut savoir s’adapter aux normes de l’énoncé !
Deux définitions de la limite d’une suite de matrices
Nous allons ici donner les deux principales définitions de la notion de limite de matrices, susceptibles d’être données par l’énoncé dans un sujet de concours. On va montrer qu’elles sont en fait équivalentes.
On se fixe \((A_n)_{n\in\mathbb N}\) une suite de matrices de \(\mathcal M_p(\mathbb R)\) et \(A\) une matrice de \(\mathcal M_p(\mathbb R)\).
Version 1 (celle de HEC 2007 ECS)
On dit que \((A_n)\) converge vers \(A\) lorsque \(\lim_{n\to+\infty}\|A_n-A\|=0\).
Dans cette version, il faut bien comprendre ce que signifie \(\|A_n-A\|\) tend vers 0. La norme d’une différence peut être interprétée comme la « distance » entre ces deux éléments (même si la notion de distance entre les matrices n’est pas très intuitive).
On est donc en train de dire que plus \(n\) est grand, plus \(A_n\) et \(A\) sont « proches ».
Version 2 (celle d’ECRICOME 2004 ECE)
On pose \(A_n=(a_{i,j}^{(n)})\) et \(A=(a_{i,j})\). On dit que \((A_n)\) converge vers \(A\) lorsque pour tout \((i,j)\in\{1,\dots,p\}^2\), la suite \((a_{i,j}^{(n)})_{n\in\mathbb N}\) converge vers \(a_{i,j}\).
Dans cette version, on dit qu’une suite de matrices \((A_n)\) converge lorsque chacun des coefficients de la suite a une limite finie quand \(n\to+\infty\). Et la limite de la suite est alors la matrice obtenue en regroupant toutes les limites des coefficients dans une matrice \(A\).
Note que dans la seconde version, il est assez clair que la limite d’une matrice si elle existe est unique. En effet, si on avait deux matrices limites distinctes, cela contredirait l’unicité de la limite dans \(\mathbb R\).
Ces deux définitions sont en fait équivalentes
Montrons ceci par double implication.
(\(\Leftarrow\)) Supposons que pour tout \((i,j)\in\{1,\dots,p\}^2\), \(\lim_{n\to+\infty} a_{i,j}^{(n)} = a_{i,j}\).
Alors pour tout \((i,j)\in\{1,\dots,p\}^2\), \(\lim_{n\to+\infty} (a_{i,j}^{(n)}-a_{i,j})=0\), donc :
\[\|A_n-A\|=\left(\sum_{i=1}^p\sum_{j=1}^p(a_{i,j}^{(n)}-a_{i,j})^2\right)^{1/2}\underset{n\to+\infty}\longrightarrow 0\]
(\(\Rightarrow\)) Supposons que \(\lim_{n\to+\infty}\|A_n-A\|=0\).
Soit \((i,j)\in\{1,\dots,p\}^2\). Pour tout \((k,\ell)\in\{1,\dots,p\}^2\), \((a_{k,\ell}^{(n)}-a_{k,\ell})^2\geq 0\), donc :
\[0\leq (a_{i,j}^{(n)}-a_{i,j})^2\leq \sum_{k=1}^p\sum_{\ell=1}^p(a_{k,\ell}^{(n)}-a_{k,\ell})^2 \underset{n\to+\infty}\longrightarrow 0\]
D’où, par encadrement : \(\lim_{n\to+\infty} a_{i,j}^{(n)} = a_{i,j}\).
Ainsi, pour la norme de Frobenius, les deux définitions sont équivalentes.
Je te laisse vérifier que c’est encore le cas pour les normes \(\|\cdot\|_1\) et \(\|\cdot\|_\infty\).
Quelques résultats connus sur les limites de matrices
1/ Limite d’une somme/d’un produit de matrices
a) Si \((A_n)_{n\in\mathbb N}\) et \((B_n)_{n\in\mathbb N}\) sont deux suites de \(\mathcal M_p(\mathbb R)\) telles que \(\lim_{n\to+\infty} A_n=A\) et \(\lim_{n\to+\infty} B_n=B\), alors :
\[ \lim_{n\to+\infty} (A_n+B_n)=A+B \]
Preuve :
Soit \((i,j)\in\{1,\dots,p\}^2\). On a \( [A_n + B_n]_{i,j} = a_{i,j}^{(n)} + b_{i,j}^{(n)} \underset{n\to+\infty}\longrightarrow a_{i,j} + b_{i,j} = [A+B]_{i,j} \) d’où le résultat.
b) Exercice : montrer que de même, la limite d’un produit de suites convergentes de matrices est le produit des limites.
2/ \(\text{GL}_p(\mathbb R)\) est dense dans \(\mathcal M_p(\mathbb R)\)
Toute matrice de \(\mathcal M_p(\mathbb R)\) est la limite d’une suite de matrices inversibles.
Preuve :
Soit \(A\in\mathcal M_p(\mathbb R)\).
Alors \(A\) admet au plus \(p\) valeurs propres distinctes.
Donc, il existe au plus un nombre fini d’entiers \(n\) tels que \(\frac1n\) est valeur propre de \(A\).
Ainsi, il existe un rang \(n_0\in\mathbb N^*\) tel que pour tout \(n\geq n_0\), la matrice \(A-\frac1n I_p\) est inversible.
On pose \(A_n=I_p\) si \(n<n_0\) et \(A_n=A-\frac1n I_p\) si \(n\geq n_0\).
La suite \((A_n)\) est donc une suite de matrices inversibles, et de plus on a pour tout \(n\geq n_0\) :
\[ A_n = \begin{pmatrix} a_{1,1} – \frac1n & a_{1,2} & \cdots & \cdots & a_{1,p} \\ a_{2,1} & a_{2,2} – \frac1n & & & \vdots \\ \vdots & & \ddots & & \vdots \\ \vdots & & & a_{p-1,p-1} – \frac1n & a_{p-1,p} \\ a_{p,1} & \cdots & \cdots & a_{p,p-1} & a_{p,p} – \frac1n \end{pmatrix} \underset{n\to+\infty}\longrightarrow \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & \cdots & a_{1,p} \\ a_{2,1} & a_{2,2} & & & \vdots \\ \vdots & & \ddots & & \vdots \\ \vdots & & & a_{p-1,p-1} & a_{p-1,p} \\ a_{p,1} & \cdots & \cdots & a_{p,p-1} & a_{p,p} \end{pmatrix} = A \]
Exponentielles de matrices
Soit \(A\in\mathcal M_p(\mathbb R)\) fixée. On s’intéresse à la convergence de la suite de matrices définie par :
\[ \forall n\in\mathbb N, \quad A_n = \sum_{k=0}^n \frac{1}{k!} A^k \]
Note la similitude de cette expression avec celle de la série exponentielle.
Lorsque cette suite converge, comme précisé précédemment, sa limite est unique, et on note \(\exp(A)\) sa limite.
Quelques exemples importants
Exemple 1
Si \(A\) est nulle, \(\exp(A)\) existe et vaut \(I_p\). En effet, pour tout \(k\geq 1\), \(A^k=0\) et de plus \(A^0=I_p\).
Exemple 2
Si \(A=I_p\) cette fois, \(\exp(I_p)\) existe et vaut \(eI_p\).
En effet :
\[\forall n\in\mathbb N, \quad A_n = \begin{pmatrix} \sum_{k=0}^n \frac{1}{k!} & 0 & \cdots & \cdots & 0 \\ 0 & \sum_{k=0}^n \frac{1}{k!} & & & \vdots \\ \vdots & & \ddots & & \vdots \\ \vdots & & & \sum_{k=0}^n \frac{1}{k!} & 0 \\ 0 & \cdots & \cdots & 0 & \sum_{k=0}^n \frac{1}{k!} \end{pmatrix} \]
Et donc, d’après la formule de la série exponentielle, la limite de chacun des coefficients diagonaux est \(e\), donc \(\lim_{n\to+\infty}A_n=eI_p\).
Exemple 2 bis
En réalité, avec le même raisonnement, on peut prouver que pour toute matrice diagonale \(D=\text{diag}(\lambda_1,\dots,\lambda_p)\), la matrice \(\exp(D)\) existe et est égale à \(\text{diag}(e^{\lambda_1},\dots,e^{\lambda_p})\).
À toi de le prouver !
Exemple 3
On suppose cette fois que \(A\) est une matrice diagonalisable.
Il existe \(P\in\text{GL}_p(\mathbb R)\) et \((\lambda_1,\dots,\lambda_p)\in\mathbb R^p\) tels que \(A=PDP^{-1}\) avec \(D=\text{diag}(\lambda_1,\dots,\lambda_p)\).
Alors :
\[A_n = \sum_{k=0}^n \frac{1}{k!} A^k = \sum_{k=0}^n \frac{1}{k!} P D^k P^{-1} = P \sum_{k=0}^n \frac{1}{k!} D^k P^{-1} \]
De plus, d’après l’exemple 2 bis, \(\lim_{n\to+\infty} \sum_{k=0}^n \frac{1}{k!} D^k = \text{diag}(e^{\lambda_1},\dots,e^{\lambda_p})\).
Donc, \((A_n)\) converge : ainsi \(\exp(A)\) existe et vaut \(P\times \text{diag}(e^{\lambda_1},\dots,e^{\lambda_p}) \times P^{-1}\).
Cas général
Nous allons montrer que toute matrice admet une exponentielle.
Pour toute matrice \(A=(a_{i,j})\in\mathcal M_p(\mathbb R)\), on pose :
\[m_A = \max_{1\leq i,j\leq p} |a_{i,j}|\]
Soient \(A=(a_{i,j}),B=(b_{i,j})\in\mathcal M_p(\mathbb R)\). Montrons que \(m_{AB}\leq pm_Am_B\).
Soit \((i,j)\in\{1,\dots,p\}^2\). On a \(\displaystyle |[AB]_{i,j}| = \left| \sum_{k=1}^p a_{i,k} b_{k,j} \right|\), d’où par inégalité triangulaire :
\[|[AB]_{i,j}| \leq \sum_{k=1}^p |a_{i,k}| |b_{k,j}| \leq \sum_{k=1}^p m_Am_B = pm_Am_B\]
En prenant le maximum, on obtient \(m_{AB}\leq pm_Am_B\).
Par une récurrence immédiate, on en déduit pour tout \(k\in\mathbb N^*\), \(m_{A^k}\leq p^{k-1} m_A^k\).
Fixons \((i,j)\in\{1,\dots,p\}^2\).
On déduit de ce qui précède que \(|[A^k]_{i,j}|\leq p^{k-1} m_A^k\). D’où :
\[0\leq\left|\left[\frac1{k!}A^k\right]_{i,j}\right|\leq \frac1p\times \frac{(pm_A)^k}{k!}\]
Or, la série \(\sum_{k\geq 0} \frac{(pm_A)^k}{k!}\) est une série exponentielle convergente (série de réels ici), ainsi \(\sum_{k\geq 0} \left[\frac1{k!}A^k\right]_{i,j}\) converge absolument, donc converge.
Autrement dit, la suite des sommes partielles \(\left(\left[\frac1{0!}A^0+\cdots+\frac1{n!}A^n\right]_{i,j}\right)_{n\in\mathbb N^*}\) converge.
Donc, la suite de matrices définie par \(A_n=\sum_{k=0}^n\frac1{k!}A^k\) converge, d’où l’existence de \(\exp(A)\).
Conclusion
Comme pour tous les thèmes hors programme, ce serait une perte de temps d’apprendre par cœur ces résultats. Il vaut mieux essayer de comprendre l’enchaînement des arguments. En revanche, si tu veux tester ta compréhension sur ce thème, je te recommande de faire les sujets suivants :
- Ecricome 2004 ECE (exercice 2), qui étudie des propriétés des exponentielles de matrices dans les cas particuliers d’une matrice nilpotente, puis d’une matrice diagonalisable.
- HEC 2007 maths 1 ECS, qui étudie les exponentielles pour une norme différente de celle que nous avons utilisée dans cet article. Attention, c’est un sujet difficile.
N’hésite pas à consulter toutes nos ressources mathématiques.