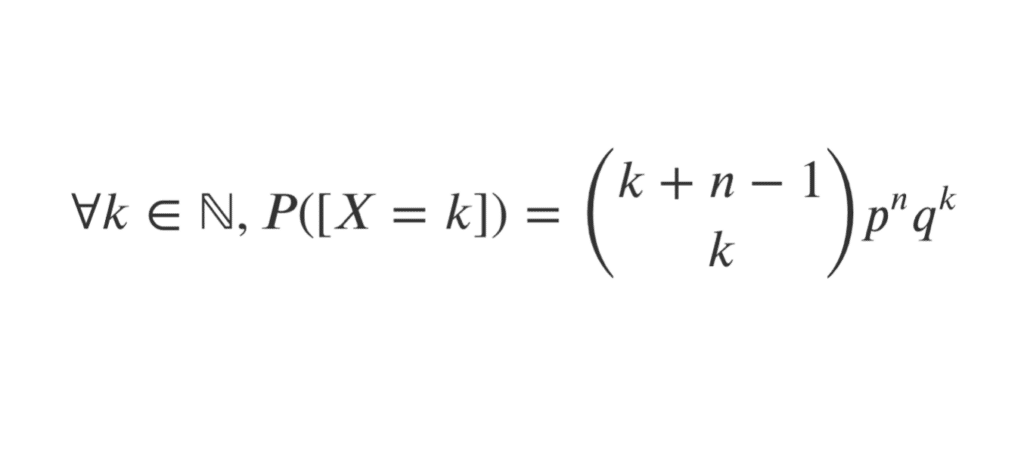Les notions hors programme se destinent surtout aux candidat·e·s visant les trois Parisiennes. Cet article t’explique donc la loi binomiale négative, loi de probabilité qui se retrouve dans de nombreux exercices, pour t’aider à mieux l’appréhender quand tu la rencontreras ! Tu pourras également retrouver une liste de propriétés liées à cette loi, ainsi que des liens vers des sujets de concours qui l’utilisent.
Dans tout cet article : \(p \in ]0,1[\) et \(n \in \mathbb N\).
La loi binomiale négative expliquée en français
La loi binomiale négative est une loi de probabilité proche de la loi géométrique. Cette dernière s’applique à une variable discrète qui compte le nombre d’essais avant d’arriver à un succès (de probabilité \(p\)).
La loi binomiale négative, elle, compte le nombre d’échecs avant d’arriver à \(n\) succès.
Exemple concret de la loi binomiale négative
Prenons l’exemple d’une pièce, qui donne pile avec la probabilité \(p\) et face avec la probabilité \(q=p-1\). Supposons ici que \(n=1\), c’est-à-dire que la variable compte le nombre d’échecs (le nombre de fois où la pièce a donné face) avant d’obtenir un succès, ici pile.
Ainsi, la variable \(X\), qui compte le nombre d’échecs avant d’obtenir un pile, suit la loi binomiale négative, et ici, nous avons : \[ \forall k \in\mathbb{N}, P([X=k])=q^{k}p\]
Définition mathématique de la loi binomiale négative
La loi binomiale négative est la loi que suit une variable aléatoire discrète \(X\), qui compte le nombre d’échecs nécessaires avant l’obtention de \(n\) succès, réalisés avec la probabilité \(p\) lors d’expériences toutes identiques et indépendantes.
Par différentes démonstrations, la loi binomiale négative se révèle suivre une loi proche de la loi binomiale. Son support est \(\mathbb{N}\), et sa loi se définit par : \[ \forall k \in\mathbb{N},P([X=k])={{k+n-1}\choose{k}}p^{n}q^{k}\] avec \(q=p-1\), \(n\) le nombre de succès et \(k\) le nombre d’échecs.
En reprenant l’exemple où \(n=1\) avec notre pièce qui donne pile avec la probabilité \(p\) et face avec la probabilité \(q\), nous retrouvons bien : \[ \forall k \in\mathbb{N},P([X=k])={{k+1-1}\choose{k}}p^{1}q^{k}=q^{k}p\]
Explication de la formule grâce au dénombrement
La formule devient un peu plus complexe quand \(n\) est différent de 1, mais elle peut s’expliquer avec du dénombrement. \(X\) compte le nombre d’échecs avant d’obtenir \(n\) succès, donc il y a au total \(n+k\) expériences. Cependant, comme la dernière donne automatiquement un succès, on ne « choisit » que \(k\) échecs parmi les \(n+k-1\) expériences.
La probabilité d’obtenir \(k\) échecs est, elle, de \(q^{k}\) et la probabilité d’obtenir les \(n\) succès est de \(p^{n}\), les expériences étant toutes des expériences identiques et indépendantes.
C’est une des manières de retrouver (et surtout de comprendre) la formule de la loi binomiale négative.
Quelques propriétés sur la loi binomiale négative
Soit \(X\) la variable aléatoire discrète comptabilisant le nombre d’échecs \(k\in\mathbb{N}\) avant d’obtenir \(n\in\mathbb{N}^{*}\) succès, avec la probabilité \(p\in]0,1[\). On la notera également \(X_n\).
- L’espérance de cette loi est égale à \(\displaystyle E(X)=\frac{nq}{p}\).
- La variance est, elle, égale à \(\displaystyle V(X)=\frac{nq}{p^{2}}\).
- La fonction de répartition est égale à \(F(k)=I_p(n,k+1)\), où \(I_p\) est la fonction bêta incomplète régularisée, c’est-à-dire que \(F(k)=\displaystyle \int_{0}^{1} t^{n-1}(1-t)^{k+1-1}\,\mathrm{d}t\).
- Par récurrence sur \(k\), on peut aussi retrouver que \(F(k)=1-q^{k+1}\displaystyle \sum_{i=0}^{n-1}{{k+i}\choose{i}}p^{i}\).
- La loi binomiale négative se note \(\mathcal{BN}(n,p)\), et on a alors \(X\hookrightarrow\)\(\mathcal{BN}(n,p)\).
- On retrouve parfois une loi alternative, celle de la loi de Pascal, appliquée à une variable aléatoire discrète Y qui compte le nombre d’essais nécessaires \(m\) avant d’obtenir \(n\) succès (dans les mêmes conditions que pour la loi binomiale négative). Ainsi, on obtient \[ \forall m \ge n,P([Y=m])={{m-1}\choose{m-n}}p^{n}q^{m-n}={{m-1}\choose{n-1}}p^{n}q^{m-n}\] Il est aisé de déduire l’une de l’autre, car il existe la relation suivante avec \(m=k+n\) : \[Y=X+n\] ce qui permet d’obtenir avec le théorème de transfert et le cours sur la variance \(\displaystyle E(X)=E(Y)-n=\frac{n}{p}-n=\frac{nq}{p}\) et \(\displaystyle V(X)=V(Y)=\frac{nq}{p^{2}}\).
- La loi binomiale négative de paramètres \(n\) et \(p=n(n+\lambda)^{-1}\) avec \(/lambda\) réel fixé strictement supérieur à 0 converge faiblement vers une loi de Poisson, elle est de paramètre \(\lambda\), quand \(n\) tend vers \(+\infty\). Cela signifie surtout que si \(X_n\hookrightarrow\)\(\mathcal{BN}(n,n(n+\lambda)^{-1})\) et que \(X\hookrightarrow\mathcal{P}(\lambda)\), alors cela donne que \(X_n\overset{\mathcal{L}}{\rightarrow}X\).
- La loi binomiale est de plus stable par somme : la somme de \(k\) variables aléatoires discrètes qui suivent toutes une loi binomiale négative de paramètres \(p\) et respectivement \((n_1,n_2,…,n_k)\), suit une loi binomiale négative de paramètres \(p\) et \(n=n_1+…+n_k\).
- D’après l’exemple au début de l’article, il existe un lien entre la loi binomiale négative et la loi géométrique : de fait, la loi géométrique s’applique à des variables discrètes qui comptabilisent le nombre de tentatives avant le premier succès, c’est-à-dire la loi binomiale négative de paramètres \(1\) et \(p\), donc \(\mathcal{G}(p)=\mathcal{BN}(1,p)\).
- L’autre loi proche de la loi binomiale négative est la loi binomiale : si on considère une variable aléatoire discrète \(Y_{k+n}\) qui suit une loi binomiale de paramètres \(k+n\) et \(p\), on obtient alors que : \[\begin{align}P([X_n\le k]&=I_p(n,k+1)\\&=1-I_{1-p}(k+1,n)\\&=1-I_{1-p}((k+n)-(n-1),(n-1)+1)\\&=1-P([Y_{k+n}\le (n-1)])\\&=P([Y_{k+n}\ge n])\end{align}\] Cette probabilité est donc égale à la probabilité qu’après \(k+n\) épreuves, il y ait au moins \(n\) succès.
Les sujets de concours utilisant la loi binomiale négative
Plusieurs sujets de concours abordent cette notion hors programme de différentes manières. Voici la liste des sujets sur lesquels tu peux t’entraîner pour te familiariser un peu plus avec cette notion (les liens mènent vers les corrigés) :