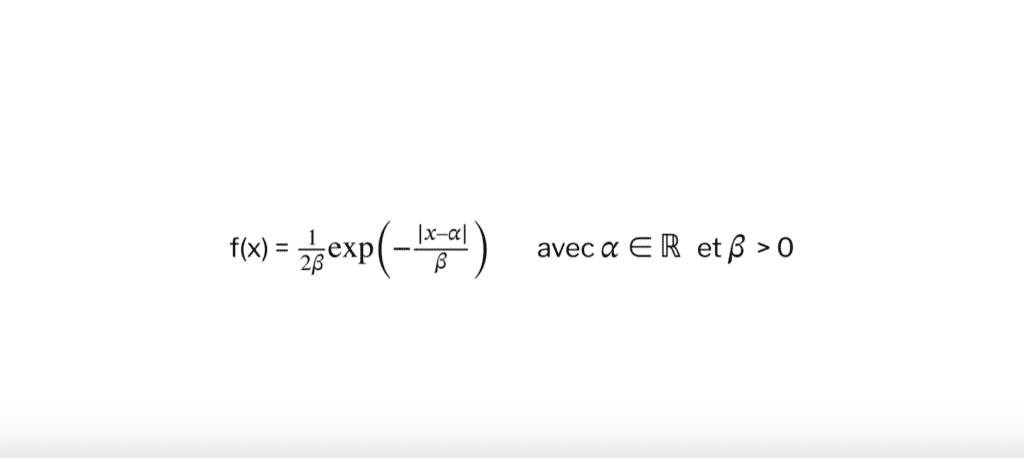On va travailler ensemble sur une loi de probabilité essentielle (mais hors programme) : la loi de Laplace. Cette loi se retrouvant dans de nombreux sujets de concours, il est important de maîtriser ses caractéristiques. C’est aussi l’occasion pour toi de revoir les méthodes des variables à densité et des lois de probabilités continues.
Présentation de la loi de Laplace
La loi de Laplace est une loi de probabilité continue à support infini. Elle est également connue sous le nom de « loi de double exponentielle », car sa densité peut correspondre à l’association de deux lois exponentielles. Cette loi permet de représenter la variabilité de phénomènes naturels et financiers (ex. : variation de prix d’actifs financiers). Elle s’illustre ainsi dans de nombreux domaines scientifiques et économiques.
Pour ta culture, Pierre-Simon Laplace (1749-1827) était un mathématicien et astronome français de renom. Il est connu pour ses travaux sur les équations différentielles, les séries infinies et la théorie des probabilités, dont la loi de Laplace est un exemple important. Laplace a également joué un rôle crucial dans la formulation de la théorie de la gravitation et a contribué à la compréhension des mouvements des corps célestes.
Définition de la loi de Laplace
On dit qu’une variable aléatoire X suit la loi de Laplace de paramètres (\( \alpha \), \( \beta \)), si elle admet comme densité la fonction f donnée par :
\( f(x) \displaystyle = \frac{1}{2 \beta} \exp\left(-\frac{|x – \alpha|}{ \beta}\right) \) avec \( \alpha \) \( \in \mathbb{R} \) et \( \beta \) > 0
Remarque : \( \alpha \) est souvent appelé le paramètre de position et \( \beta \) le paramètre d’échelle.
Tu peux t’entraîner à montrer que la fonction f est bien une densité de probabilité, voici quelques conseils :
- Tu peux facilement vérifier la positivité (fonction valeur absolue) et démontrer la continuité en \( \alpha \) et sur le reste de l’espace \( \mathbb{R} \).
- Pour montrer que l’intégrale de f sur \( \mathbb{R} \) est égale à 1 : sépare les deux cas \( x \geq \alpha \) et x < \( \alpha\), puis additionne les deux résultats obtenus.
Fonction de répartition de la loi de Laplace
La fonction de répartition F(x) d’une variable aléatoire X suivant la loi de Laplace (qui, pour rappel, correspond à la probabilité que X prenne une valeur inférieure ou égale à x) est définie par :
\( F(x) = \begin{cases} \frac{1}{2} \exp\left(\frac{x – \alpha}{\beta}\right) & \text{si } x \leq \alpha \\ 1 – \frac{1}{2} \exp\left(-\frac{x – \alpha}{\beta}\right) & \text{si } x > \alpha \end{cases} \)
Espérance et variance de la loi de Laplace
Une variable suivant la loi de Laplace admet toujours une espérance, car la densité de probabilité de la loi de Laplace est bien définie pour tout \( \alpha \) \( \in \mathbb{R} \). Elle admet une variance uniquement si \( \beta \) > 0.
Calcul de l’espérance
Pour trouver l’espérance d’une variable aléatoire suivant la loi de Laplace, il faut là aussi séparer l’intégrale en deux cas \( x \geq \alpha \) et x < \( \alpha\). On a donc :
\( \begin{align} \mathbb{E}[X] &= \int_{-\infty}^{\infty} x \cdot f(x) \, dx \\ \mathbb{E}[X] &= \int_{-\infty}^{\alpha} x \cdot \frac{1}{2\beta} \exp\left(-\frac{ \alpha – x}{\beta}\right) \, dx + \int_{\alpha}^{\infty} x \cdot \frac{1}{2 \beta} \exp\left(-\frac{x – \alpha }{ \beta}\right) \, dx \end{align} \)
Après calculs, on trouve alors que l’espérance d’une variable suivant la loi de Laplace est égale à :
\( \mathbb{E}[X] = \left( \alpha \cdot \frac{ 1}{2} + \frac{ \beta}{2}\right) + \left(\alpha \cdot \frac{1}{2} – \frac{ \beta}{2}\right) = \alpha \)
L’espérance de la loi de Laplace est donc \( \mathbb{E}[X] = \alpha \).
Calcul de la variance
Pour trouver la variance d’une variable aléatoire suivant la loi de Laplace, on utilise la formule (bien connue) de König \( \text{V}(X) = \mathbb{E}[X^2] – (\mathbb{E}[X])^2 \). On sait déjà que l’espérance est égale à \( \alpha \). Pour calculer \( (\mathbb{E}[X])^2 \), on sépare à nouveau l’intégrale en deux cas \( x \geq \alpha \) et x < \( \alpha\). On a donc :
\(\displaystyle \mathbb{E}[X^2] = \int_{-\infty}^{\alpha} x^2 \cdot \frac{1}{2\beta} \exp\left(-\frac{\alpha – x}{\beta}\right) \, dx + \int_{\alpha}^{\infty} x^2 \cdot \frac{1}{2\beta} \exp\left(-\frac{x – \alpha}{\beta}\right) \, dx \)
\(\displaystyle \mathbb{E}[X^2] = \alpha^2 + 2\beta^2 \)
Par la formule de König, on trouve alors :
\( \text{V}(X) = \mathbb{E}[X^2] – (\mathbb{E}[X])^2 = (\alpha^2 + 2\beta^2) – \alpha^2 = 2\beta^2 \)
La variance de la loi de Laplace est donc \( \text{V}(X) = 2\beta^2 \).
Quelques astuces sur la loi de Laplace
Si on pose une variable aléatoire réelle Y = \( \beta \)X +\( \alpha \) avec X une variable aléatoire qui suit la loi de Laplace de paramètres (0,1), alors on peut montrer assez facilement que la variable Y suit en réalité la loi de Laplace de paramètres (\( \alpha \), \( \beta \)).
Pour trouver l’espérance et la variance plus facilement d’une variable aléatoire réelle Y qui suit la loi de Laplace de paramètres (\( \alpha \), \( \beta \)), tu peux donc d’abord passer par l’espérance et la variance d’une variable aléatoire X qui suit la loi de Laplace de paramètres (0,1).
Représentation graphique de la loi de Laplace (Python)
Les sujets de concours faisant de plus en plus intervenir des exercices avec du Python, il peut être utile de maîtriser la loi de Laplace aussi dans ce langage, en particulier sa représentation graphique.
Voici tout d’abord le code Python qui permet d’écrire la densité d’une variable suivant la loi de Laplace (que tu connais désormais) :
En utilisant à nouveau la fonction laplace_pdf (PDF = Probability Density Function) définie ci-dessus, on est alors capable d’écrire en langage Python la représentation graphique de cette densité. On prendra alors ici les valeurs 0 pour \( \alpha \) et 1 pour \( \beta \) :
Remarque : inutile de connaître ces deux codes Python par cœur, mais tu peux essayer de les comprendre au cas où il te serait demandé de compléter des codes similaires dans un sujet de concours. Tu peux par ailleurs retrouver ici tous nos autres articles consacrés au langage Python.
Annales où tu pourras retrouver la loi de Laplace
Cette loi est d’autant plus utile à travailler qu’elle est déjà tombée aux concours de maths appliquées. Je te mets ici les liens des sujets :
- Maths III HEC 2007 Problème Partie I
- Maths I-III ESSEC 2014 Partie 3 (3a)
- Maths I-III ESSEC 2017 Partie I
Ce dernier sujet est par ailleurs très intéressant puisqu’il met aussi en jeu les lois \( \epsilon \)-différentielles (très intéressantes même si elles aussi sont hors programme).
Et tu peux retrouver ici les corrigés de ces sujets :
Conclusion
Voilà, tu connais maintenant tout sur la loi de Laplace ! Tu es désormais capable de donner sa fonction de répartition, son espérance, sa variance et même d’écrire sa densité et sa représentation graphique sur Python.
J’espère que cet article t’a plu. Tu peux retrouver ici toutes nos autres ressources mathématiques et continuer à t’exercer sur d’autres annales grâce à notre méga-répertoire.