Dans cet article, nous allons nous intéresser à un classique des annales : la loi log-normale. L’étude de cette loi peut survenir aussi bien en mathématiques approfondies qu’en mathématiques appliquées, et on la retrouve dans des annales de Parisiennes comme dans des annales de l’EMLyon ou de l’EDHEC.
Présentation de la loi
Une variable aléatoire \(X\) suit la loi log-normale de paramètres \((m,\sigma)\) si \(Y=\ln(X)\) suit la loi \(X \hookrightarrow\mathcal{N}(m,\sigma^2) \).
Pour simplifier les calculs, comme nous connaissons les propriétés des lois normales, nous allons étudier \(X=e^{Y}\) pour découvrir les propriétés de la loi log-normale.
Fonction de répartition et densité
On note \(\Phi\) la fonction de répartition de \(Y\).
Tout d’abord, \(X(\Omega)=\mathbb{R}_{+}^{*}\).
Ainsi, en notant \(F_X\) la fonction de répartition de \(X\), on a \(\forall x \in\mathbb{R}_{-}\), \(F_X(x)=0\).
\(\forall x \in\mathbb{R}_{+}^{*}\), \(F_X(x)=P(e^{Y}\le x) = P(Y \le \ln(x)) = \Phi(\ln(x)) \)
Donc, \(F_X(x) =\begin{cases}0 &\text{si} \; x \le 0\\\Phi(\ln(x)) &\text{sinon}\end{cases}\) et \(F_X\) est bien continue sur \(\mathbb{R}\) par continuité de la fonction logarithme.
On peut alors trouver une densité de \(X\) que l’on note \(f_X\). On obtient \(f_X(x) =\begin{cases}0 &\text{si} \; x \le 0\\\frac{e^{-\frac{1}{2}(\frac{\ln(x)-m}{\sigma})^2}}{\sqrt{2\pi} \sigma x} &\text{sinon}\end{cases}\).
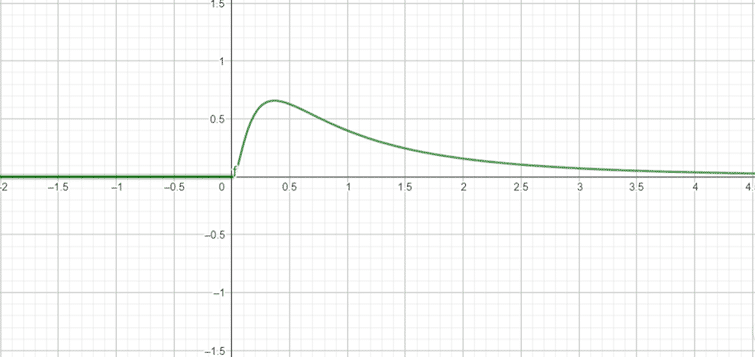
Représentation graphique
En prenant les paramètres \(m=0\) et \(\sigma=1\), on obtient cette représentation graphique de \(f_X\) :
Espérance
\(X\) admet bien une espérance et pour la calculer, on utilise un théorème de transfert et la méthode de la factorisation canonique :
\( \begin{align} E(X)=E(e^Y) & =\displaystyle \int_{-\infty}^{+\infty} e^t \frac{e^{-\frac{1}{2}(\frac{x-m}{\sigma})^2}}{\sqrt{2\pi} \sigma} \, \mathrm{d}t \\&= \displaystyle \int_{-\infty}^{+\infty} \frac{e^{\frac{2\sigma^2t-t^2+2tm -m^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma} \, \mathrm{d}t \\&= \displaystyle \int_{-\infty}^{+\infty} \frac{e^{-\frac{1}{2}(\frac{t-(m+\sigma^2)}{\sigma})^2 +\frac{2m\sigma^2+\sigma^4}{2\sigma^2}}}{\sqrt{2\pi}\sigma} \, \mathrm{d}t \\&= e^{m+\frac{\sigma^2}{2}} \underbrace{\displaystyle \int_{-\infty}^{+\infty} \frac{e^{-\frac{1}{2}(\frac{t-(m+\sigma^2)}{\sigma})^2 }}{\sqrt{2\pi}\sigma} \, \mathrm{d}t}_{=1 (\text{on reconnaît la densité d’une loi} \mathcal{N}(m+\sigma^2,
\sigma^2))} \\&= e^{m+\frac{\sigma^2}{2}} \end{align}\).
Ainsi, \(E(X)=e^{m+\frac{\sigma^2}{2}}\).
Variance
Pour calculer la variance de \(X\), on utilise la formule de König-Huygens. Nous devons alors trouver l’espérance de \(X^2\).
\(E(X^2)=E(e^{2Y})\). Or \(2Y \hookrightarrow\mathcal{N}(2m,(2\sigma)^2) \), ainsi, on obtient \(E(X^2)=e^{2m+\frac{(2\sigma)^2}{2}}=e^{2m+2\sigma^2}\).
Donc, \(V(X)=E(X^2)-(E(X))^2=e^{2m+2\sigma^2}-e^{2m+\sigma^2} = e^{2m+\sigma^2}(e^{\sigma^2}-1)\).
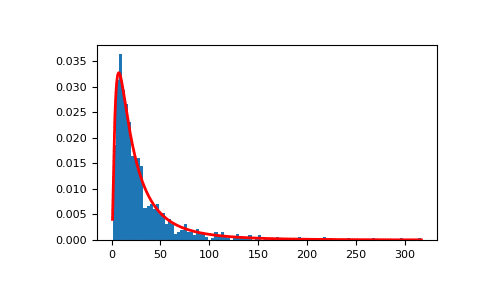
En python
Pour simuler une loi log-normale sur Python, on utilise son lien avec la loi normale dont on peut utiliser la commande. Ainsi un programme type qui simulerait cette loi serait du type :
Voici l’histogramme de cette loi sorti par Python :
N.B. : il existe une commande déjà enregistrée par python qui est hors programme ECG, c’est la commande :
Pour t’entraîner
En mathématiques appliquées, le sujet de Mathématiques 1 de 2012 traite des propriétés des lois log-normales en partie 1 (sujet, corrigé)
En mathématiques approfondies, tu peux t’entraîner à refaire les démonstrations de l’espérance et de la variance en prenant des valeurs particulières de \(m\) et de \(\sigma\). Par exemple, tente de montrer que pour \(m=0\) et \(\sigma=1\), \(E(X)=\sqrt{e}\).
Tu peux retrouver toutes nos ressources de mathématiques ici !