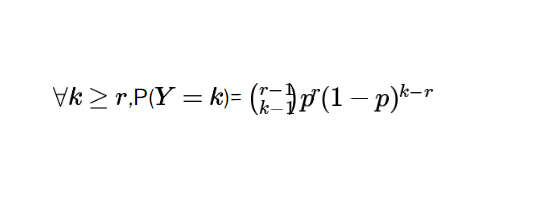Les notions hors programme se destinent surtout aux candidats visant les trois Parisiennes. Cet article t’explique donc la loi de Pascal, loi de probabilité qui se retrouve dans de nombreux exercices, pour t’aider à mieux l’appréhender quand tu la rencontreras ! Tu pourras également trouver des liens vers des articles traitant de notions qui se rapprochent de cette loi.
Dans tout cet article, soient \(p \in ]0,1[ , n \in \mathbb N\)
Explication en français de la loi de Pascal
On considère un schéma de Bernoulli, c’est-à-dire une expérience aléatoire à deux issues : succès (de probabilité \(p\)) ou échec (de probabilité \(1-p\), souvent appelé \(q\) ). Ce schéma est répété \(n\) fois de façons identiques et indépendantes. Soit la variable aléatoire \(X\), qui donne le rang d’apparition du premier succès (on parle aussi de temps d’attente du premier succès). On dit que \(X\) suit une loi géométrique de paramètre p, \(X \hookrightarrow
\mathcal{G}(p)\).
Soit \(Y\) le nombre de tirages nécessaires pour l’obtention du r-ième succès (r≥1). On dit que \(Y\) suit la loi de Pascal de paramètres \(r\) et \(p\).
Explication mathématique de la loi de Pascal
Soit \(Y\) une variable aléatoire qui suit une loi de Pascal de paramètres \(r\) et \(p\), on note alors : \(Y\hookrightarrow \mathcal P(r,p)\), sa loi de probabilité est définie par :
\(Y(\Omega)=\{r,r+1,\dots\}\)
\(\forall k \ge r\),P(\(Y=k\))= \({ {r-1}\choose{k-1} } p^r(1-p)^{k-r}\)
\(Y\) admet alors une espérance et une variance données par : \(E(Y)=\frac rp\textrm{ et }V(Y)=\frac{r(1-p)}{p^2}\)
Démonstration de la formule de la loi et de l’espérance
Il y a plusieurs façons de démontrer cette formule : avec des événements, par dénombrement ou encore par récurrence (sur \(r\)).
Voici ci-dessous une des démonstrations possibles : la démonstration par événements.
Démonstration de la formule de la loi
Soit \( k \ge r\). [\(Y=k\)] se réalise si et seulement si on obtient le r-ième pile au k-ième lancer. On note \(Z\) la variable aléatoire égale au nombre de « pile » obtenu au cours des \( k-1\) premiers lancers et \(P_k\) l’événement : « obtenir pile au k-ième lancer ». On a donc :
[\(Y=k\)]=[\(Z=r-1\)]\(\cap\) \(P_k\)
De plus, les lancers sont indépendants, donc les événements le sont aussi :
\(P(Y=k)=P(Z=r-1)P(P_k)\)
\( Z\) est la variable aléatoire égale au nombre de succès (obtenir « pile ») au cours de \(k-1\) lancers indépendants donnant tous « pile » avec la probabilité \(p\), donc \(Z\) suit la loi binomiale \( \hookrightarrow
\mathcal{B}(k-1,p)\) et \(\forall k \ge r\),P(\(Y=k\))= \({{r-1}\choose{k-1}} p^r(1-p)^{k-r}\)
Démonstration de l’espérance
Soit \(Y’\) une variable suivant une loi de Pascal de paramètres \(r+1\) et \(p\). Y est une variable prenant ses valeurs pour tout \( k \in[\![r,+\infty]\!]\). L’espérance de \(Y\) existe si et seulement si la série de terme général \(k P(Y=k)\) converge.
On observe que : \(\forall k \ge r\), k P(\(Y=k\)) = \( k{{k-1}\choose{r-1}} p^r(1-p)^{k-r}\) = \(r{{k}\choose{r}}p^r(1-p)^{k-r}\) = \(\frac{r}{p}{{k}\choose{r}}p^{r+1}(1-p)^{k+1-(r+1)}\) = \(\frac{r}{p}\)P(\(Y’=k+1)\)
On sait que \(Y’\) est une variable qui prend ses valeurs dans \( \in[\![r+1,+\infty]\!]\). La série\(\displaystyle \sum_{k=r+1}^{+\infty} P(Y’=k+1)\) converge donc et sa somme vaut \(1\). On en déduit que la série de terme général \(k P(Y=k\)) est convergente.
On en déduit aussi que : \(\displaystyle \sum_{k=r}^{+\infty}k P(Y=k)\) = \(\frac{r}{p}\displaystyle \sum_{k=r}^{+\infty} P(Y’=k+1\)) = \(\frac{r}{p}\)
Ce qui démontre que : \(Y\) admet une espérance et : \(E(Y)=\frac rp\textrm{ }\)
Liens vers des sujets d’annales liés à cette notion
Plusieurs sujets de concours abordent cette notion hors programme. Voici la liste des sujets sur lesquels tu peux t’entraîner pour te familiariser un peu plus avec cette notion (les liens mènent vers les corrigés) :
Conclusion
Tu connais maintenant la loi de Pascal, tu sais démontrer sa formule (comme c’est une notion hors programme, si tu la rencontres, je compte sur toi pour refaire la démonstration) et dans quel type de problème on peut la rencontrer.
Voilà ! Cet article de Major-prépa portant sur la loi de Pascal touche à sa fin, j’espère qu’il t’aura été utile. N’hésite pas à consulter toutes nos ressources mathématiques !