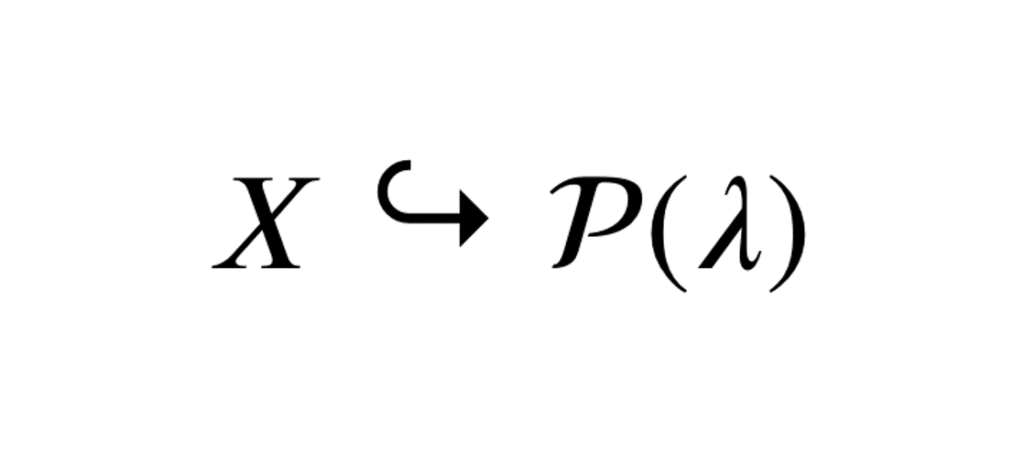La loi de Poisson est un grand classique du concours (que l’on doit au célèbre mathématicien Denis Poisson). Il est donc nécessaire de maîtriser les bases, mais aussi les plus fines subtilités de cette notion. Major-Prépa est là pour t’aider. Voici ce qu’il y a à savoir. On prendra pour tout le long de cet article \( n \in \mathbb{N}\)et \( p \in \mathbb{[0,1]}\).
Petit point d’histoire sur Poisson
Denis Poisson (1781-1840) est un mathématicien, géomètre et physicien français du XIXe siècle. Il a été reconnu par ses pairs pour ses travaux remarquables. En témoignage de cette reconnaissance, son nom figure parmi les 72 personnalités — scientifiques, ingénieurs et industriels — inscrites par Gustave Eiffel sur la tour Eiffel.
En 1838, Poisson introduit la loi de Poisson dans son ouvrage Recherches sur la probabilité des jugements en matière criminelle et en matière civile. Cette loi est aujourd’hui un outil fondamental en théorie des probabilités et en statistique, largement utilisée pour modéliser des phénomènes aléatoires rares ou espacés.
Modèle de la loi de Poisson
La loi de Poisson ne possède pas de modèle à part entière, mais est applicable à diverses situations. Notamment celles impliquant l’étude de flux sur une période déterminée. Dans la plupart des exercices, les paramètres de la loi de Poisson sont fournis.
Définition et formule de la loi de Poisson
Une variable aléatoire \( X \) suit une loi de Poisson de paramètre \( \lambda \) (où \( \lambda \in \mathbb{R}_{+}^{*}\)) si :
\[
X(\Omega) = \mathbb{N} \quad \text{et} \quad \forall k \in \mathbb{N}, \quad P(X=k) = e^{-\lambda} \frac{\lambda^k}{k!}
\]
On note alors \( X \hookrightarrow \mathcal{P}(\lambda) \).
Quelques propriétés de la loi de Poisson
Démonstration de l’espérance et de la variance
Soit \( X \) une variable aléatoire suivant une loi de Poisson de paramètre \( \lambda \).
\begin{align}
\mathbb{E}(X) &= \sum_{k=0}^{\infty} k \cdot \frac{\lambda^k e^{-\lambda}}{k!} \\
&= \sum_{k=1}^{\infty} k \cdot \frac{\lambda^k e^{-\lambda}}{k!} \\
&= \lambda e^{-\lambda} \sum_{k=1}^{\infty} \frac{\lambda^{k-1}}{(k-1)!} \\
&= \lambda e^{-\lambda} \sum_{j=0}^{\infty} \frac{\lambda^j}{j!} \quad (j = k-1) \\
&= \lambda e^{-\lambda} e^{\lambda} \\
&= \lambda
\end{align}
D’où : \( \fbox{ \(\mathbb{E}(X) = \lambda \)} \)
Pour la variance, on calcule \( \mathbb{E}(X^2) \) pour utiliser la formule de König-Huygens :
\[
\text{Var}(X) = \mathbb{E}(X^2) – (\mathbb{E}(X))^2
\]
\begin{align}
\mathbb{E}(X^2) &= \sum_{k=0}^{\infty} k^2 \cdot P(X = k) \\
&= \sum_{k=0}^{\infty} k^2 \cdot \frac{\lambda^k e^{-\lambda}}{k!} \\
&= \sum_{k=0}^{\infty} (k(k – 1) + k) \cdot \frac{\lambda^k e^{-\lambda}}{k!} \\
&= \sum_{k=0}^{\infty} k(k – 1) \frac{\lambda^k e^{-\lambda}}{k!} + \sum_{k=0}^{\infty} k \frac{\lambda^k e^{-\lambda}}{k!} \\
&= \lambda^2 e^{-\lambda} \sum_{j=0}^{\infty} \frac{\lambda^j}{j!} + \lambda \\
&= \lambda^2 + \lambda
\end{align}
D’où :
\[
\text{Var}(X) = \mathbb{E}(X^2) – (\mathbb{E}(X))^2 = \lambda^2 + \lambda – \lambda^2 = \lambda
\]
Ainsi : \( \fbox{\( \text{Var}(X) = \lambda \)} \)
Approximation de la loi binomiale par la loi de Poisson
Contrairement à la loi de Poisson, qui a un paramètre \( \lambda\), la loi binomiale est caractérisée par deux paramètres : \(n\) (le nombre d’épreuves) et \(p\) (la probabilité de succès).
Mais quel est le lien avec la loi de Poisson ? Sous certaines conditions, une loi binomiale peut être approximée par une loi de Poisson si :
\(n ≥ 30 \) : le nombre d’épreuves est suffisamment grand.
\(p≤0,1 \) : la probabilité de succès est assez petite.
\(np<15 \) : l’espérance d’avoir un succès reste faible.
Ces conditions signifient que lorsqu’on a un grand nombre d’épreuves avec une faible probabilité de succès, on parle d’un phénomène rare. Dans ce cas, on peut approximativement utiliser la loi de Poisson pour simplifier les calculs.
Dans ce cas, si \(X \hookrightarrow \mathcal{B}(n,p) \), alors \(X\) peut être approchée par \(X \hookrightarrow \mathcal{P}(np)\) soit \(X \hookrightarrow \mathcal{P}(\mathbb{E}(X))\)
Approximation de la loi de Poisson par la loi normale
Lorsque le paramètre \( \lambda\) de la loi de Poisson est grand (généralement supérieur à 15), la distribution de Poisson peut être approximée par une loi normale. Cette approximation est utile, car la loi normale est plus facile à manipuler mathématiquement, en particulier pour les calculs de probabilités.
Paramètres de la loi normale approximative
L’espérance \(\mu = \lambda\)
La variance \(\sigma^2 = \lambda\)
Formule de la loi normale
La variable aléatoire \(X\) suivant une loi normale avec espérance \(\lambda\) et variance \(\lambda\) est notée \(X \sim \mathcal{N}(\lambda, \lambda)\). La densité de probabilité est donnée par :
\[
f(x) = \frac{1}{\sqrt{2 \pi \lambda}} \exp\left(-\frac{(x – \lambda)^2}{2\lambda}\right)
\]
Exercice
Dans un supermarché, le nombre de clients passant à une caisse par heure suit une loi de Poisson avec un paramètre \( \lambda = 15 \).
Questions
- Quelle est la probabilité que la caisse enregistre exactement 20 clients en une heure ?
- Quelle est la probabilité que la caisse enregistre au plus 10 clients en une heure ?
- Utilisez la loi normale pour approximer la probabilité d’avoir entre 12 et 18 clients en une heure. Justifiez l’utilisation de la loi normale et effectuez les calculs nécessaires.
- Supposons que le nombre de clients par heure puisse également être modélisé par une loi binomiale avec \( n = 30 \) essais et une probabilité de succès \( p = 0,5 \). Montrez que, sous ces conditions, la loi binomiale peut être approximée par la loi de Poisson et comparez les probabilités d’avoir exactement 15 clients avec les deux lois.
Solutions
Question 1
Ici, on calcule \( P(X = 20) = \frac{e^{-15} \cdot 5^{20}}{20!} \)
Ainsi, \( \fbox{P(X = 20) ≈ 0,0381} \)
Question 2
La probabilité d’avoir au plus 10 clients est :
\(\begin{align}
P(X \leq 10) &= \sum_{k=0}^{10} P(X = k) \\
&= \sum_{k=0}^{10} \frac{e^{-15} \cdot 15^k}{k!} \\
\end{align} \)
Donc, \( \fbox{\(P(X \leq 10) \approx 0,2231\)} \)
Question 3
On commence par justifier l’utilisation de la loi normale.
Ici, \(\lambda = 15\), ce qui est suffisamment grand pour utiliser cette approximation.
Paramètres de la loi normale approximative :
\[
\text{Espérance} \, (\mu) = \lambda = 15
\]
\[
\text{Variance} \, (\sigma^2) = \lambda = 15
\]
\[
\text{Écart-type} \, (\sigma) = \sqrt{\lambda} = \sqrt{15} \approx 3,87
\]
Nous souhaitons calculer : \(P(12 \leq X \leq 18)\)
On a : \( X \sim N(15, 15) \)
On cherche à se ramener à une loi normale.
On pose Z = \( \frac{X-15}{\sqrt{15}}\)
\[
P(12 \leq X \leq 18)= \left(\frac{12 – 15}{\sqrt{15}} \leq Z \leq \frac{18 – 15}{\sqrt{15}}\right)
\]
Calculons les bornes :
\[
\frac{12 – 15}{\sqrt{15}} \approx \frac{-3}{3,87} \approx -0,78
\]
\[
\frac{18 – 15}{\sqrt{15}} \approx \frac{3}{3,87} \approx 0,78
\]
Ainsi :
\(
\begin{align}
P(12 \leq X \leq 18) & \approx P(-0,78 \leq Z \leq 0,78) \\
& \approx \Phi(0,90) – \Phi(-0,90) \\
& \approx 0,5420
\end{align}
\)
Donc, la probabilité d’avoir entre 12 et 18 clients en une heure est d’environ \( \fbox{\(54 \%\)} \)
Question 4
On compare les deux méthodes.
En utilisant la loi binomiale avec \( n = 30 \) et \(p = 0,5 \)
On a alors : \( X \hookrightarrow
\mathcal{B}(30 , 0,5) \)
Donc :
\[
\begin{align}
P(X = 15) = &\binom{30}{15} (0,5)^{30} \\
& \approx 0,144
\end{align}\]
On obtient donc \( \fbox{\(P(X =15) \approx 0,144\)} \)
On cherche maintenant à calculer \( P(X = 15) \) en utilisant une approximation par la loi de Poisson.
On a : \(\lambda = np = 15 \).
Soit :
\[
\begin{align}
P(X = 15) & \approx \frac{e^{-15} \cdot 15^{15}}{15!} \\
& \approx 0,1024
\end{align}
\]
On obtient donc ici \( \fbox{\(P(X=15) \approx 0,1024\)} \)
On remarque une légère différence entre ces deux méthodes, il y a une marge d’erreur à considérer.
N’hésite pas à faire et à refaire des exercices classiques sur la loi de Poisson pour ensuite te tester sur des problèmes plus compliqués. Ne panique pas si tu n’as pas tout compris dès le départ, cela viendra à force de t’exercer !
Notions hors programme en rapport avec la loi de Poisson
La loi de Poisson a donné lieu à de nombreuses notions hors programme (qui se trouvent régulièrement dans les sujets). Parmi elles, tu peux retrouver :
- Modes d’une distribution poissonnienne (hors programme ECG)
- Le processus de Poisson (hors programme ECG)
Tu peux aussi consulter nos autres articles pour parfaitement maîtriser les probabilités :
- Fiche sur les probabilités
- Trois astuces sur les probabilités discrètes
- Cinq liens entre les lois de probabilité
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés ! Tu peux également accéder ici à toutes nos autres ressources mathématiques !