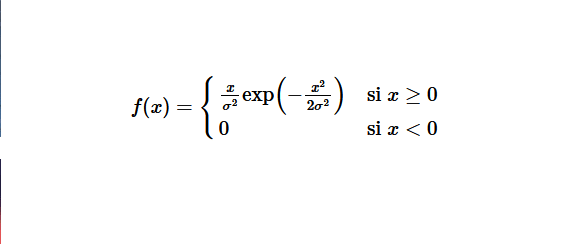Nous allons nous intéresser à une loi de probabilité hors programme qui tombe régulièrement aux concours écrits qui est la loi de Rayleigh. Généralement, les notions hors programme s’adressent aux étudiants visant les écoles du top 3. Mais cette loi tombe assez régulièrement dans des sujets EDHEC/EML. Cette loi est une loi continue. Elle te permettra de revoir les calculs classiques pour les variables aléatoires à densité !
Définition de la loi de Rayleigh
La loi de Rayleigh est un cas particulier de la loi de Weibull avec \( k=2 \ \text{et} \ \lambda=\sigma\).
On dit qu’une variable aléatoire \(X\) suit la loi de Rayleigh de paramètre \(\sigma\), si elle admet comme densité la fonction \(f\) donnée par :
\( \displaystyle f(x) =
\begin{cases}
\frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right)&\text{si} \; x \ge 0
\\
0 &\text{si} \; x < 0
\end{cases} \)
\(\quad \text{Avec} \ \sigma >0 \ \text{un paramètre quelconque (ce n’est pas une variance ou un écart-type)} \)
Il est rapide de montrer que cette fonction est bien à densité :
- \(f\) est continue sur \(\mathbb{R}\) comme produit et composée de fonctions continues sauf éventuellement en \(0\)
- \(f\) est aussi positive sur \(\mathbb{R}\) soit par produit, soit parce qu’elle est nulle
- Sous convergence de l’intégrale, on a :\(\displaystyle \int_{-\infty}^{+\infty} f(x) \, \mathrm{dx} =\int_{0}^{+\infty} \frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right) \, \mathrm{dx}\).
Or, soit \( \text{A} >0, \)
\( \begin{align} \displaystyle \int_{0}^{A} \frac{x}{\sigma^2} \exp\left(-\frac{x^2}{2\sigma^2}\right) \, \mathrm{dx}\ &=\displaystyle \left[-\exp\left(-\frac{x^2}{2\sigma^2}\right)\right]_{0}^{A}
\\ & = -\exp\left(-\frac{A^2}{2\sigma^2}\right) \ + \exp(0)
\end{align}\)
\( \text{Et}, \ \lim \limits_{A \to +\infty} \displaystyle -\frac{A^2}{2\sigma^2} = – \infty \ \text{donc} \ \lim \limits_{n \to +\infty}e^{X}=0
\)
Donc, on a bien \(\lim \limits_{A \to +\infty} \displaystyle \exp(-\frac{A^2}{2\sigma^2}) = 1 \ \text{et} \ \displaystyle \int_{-\infty}^{+\infty} f(x) \, \mathrm{dx} =1 \)
Fonction de répartition
Déterminons la fonction de réparation de la loi de Rayleigh :
- \(\forall \ x<0\) : \( f\) est nulle sur \( ]-\infty,0[\), donc \(F(x) = 0\)
- \(\forall \ x \in\mathbb{R}^+\),
\(\begin{align} \displaystyle F(x) &=\int_{-\infty}^{x}f(t) \, \mathrm{dt} \\&=\int_{0}^{x} \frac{t}{\sigma^2} \exp\left(-\frac{t^2}{2\sigma^2}\right) \, \mathrm{dt}
\\&=\displaystyle \left[-\exp\left(-\frac{t^2}{2\sigma^2}\right)\right]_{0}^{x}
\\ & = 1 -\exp\left(-\frac{x^2}{2\sigma^2}\right) \
\end{align}\)
La fonction de répartition de la loi de Rayleigh est donc : \(
\forall x \in \mathbb{R}, \quad \fbox {\(F(x) =
\begin{cases}
1 – e^{-\frac{x^2}{2\sigma^2}} & \text{si } x \ge 0, \\
0 & \text{si } x < 0.
\end{cases}\)}
\)
Lien avec d’autres lois
La loi de Rayleigh est liée avec la loi normale et la loi du Khi 2. Je te laisse lire cet article si tu veux en savoir plus !
La loi de Rayleigh est aussi liée à la loi exponentielle. En effet, si \(X\hookrightarrow\mathcal{E}(\lambda)\), alors \( Y=\sqrt{2X\sigma^2\lambda} \) suit la loi de Rayleigh de paramètre \(\sigma\).
Démonstration
Soit \(X\hookrightarrow\mathcal{E}(\lambda)\) et \( Y= \displaystyle \sqrt{2X\sigma^2\lambda} \). Déterminons la fonction de répartition de Y.
Y est une variable aléatoire positive, donc : \(\forall x <0, \; F_Y(x) = 0\)
\( \begin{align*} \text{Et,} \ \forall x \in\mathbb{R}_{+}, \
F_Y(x) &= P(Y \leq x) \\
&= P\left(\sqrt{2X\sigma^2\lambda} \leq x\right) \\
&= P\left(X \leq \frac{x^2}{2\sigma^2\lambda}\right) \\
&= F_X\left(\frac{x^2}{2\sigma^2\lambda}\right)\\
&= 1 – e^{-\lambda \cdot \frac{x^2}{2\sigma^2\lambda}} \\
&= 1 – e^{-\frac{x^2}{2\sigma^2}}.
\end{align*}\)
On retrouve bien \(F_Y(y) =
\begin{cases}
0 & \text{si } x < 0, \\
1 – e^{-\frac{x^2}{\sigma^2}} & \text{si } x \geq 0.
\end{cases}\) qui est la fonction de répartition d’une loi de Rayleigh de paramètre \(\sigma\).
On peut alors facilement simuler la loi de Rayleigh sur Python à l’aide de la loi exponentielle :
On n’a pas besoin de faire intervenir un \(\lambda\), car si \( X \hookrightarrow \mathcal{E}(1), \ Y= \displaystyle \sqrt{2X\sigma^2\lambda}\) suit la loi de Rayleigh de paramètre \(\sigma\).
Espérance
Pour trouver l’espérance d’une variable X suivant la loi de Rayleigh, on peut utiliser la loi normale :
En effet, soit \(Z \hookrightarrow \mathcal{N}(0,\sigma^2) \), sa densité est donc \(f_Z(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{x^2}{2\sigma^2}}\). Or, d’après le cours, on sait que Z admet une variance et donc un moment d’ordre 2 qui vaut \(E(X^2)=V(X)-E(X)=\sigma-0=\sigma\).
De plus, la fonction \(x \mapsto x^2.f_Z(x)\) est paire, ce qui signifie que : \(\displaystyle\int_{0}^{+\infty} x^2 f_Z(x) \, dx = \frac{1}{2}E(Z^2)\).
La variable aléatoire \( X \) admet une espérance si et seulement si l’intégrale
\[
\int_{-\infty}^{+\infty} x f_X(x) \, dx
\]
est absolument convergente. Comme \( f \) est nulle sur \( ]-\infty, 0] \) et positive sur \( [0, +\infty[ \), cela revient à prouver la convergence simple de l’intégrale :
\[
\int_{0}^{+\infty} x^2 e^{-\frac{x^2}{2\sigma^2}} \, dx =\frac{\sqrt{2 \pi }}{2} \times E(Z^2) = \sigma\sqrt{\frac{\pi }{2}}.
\]
Donc, \( X \) admet une espérance qui vaut \( \displaystyle
E(X) =\sigma \sqrt{\frac{\pi }{2}}. \)
Variance
Pour déterminer la variance de X suivant la loi de Rayleigh, il nous faut d’abord déterminer \(E(X^2)\). Pour cela, nous pouvons utiliser son lien avec la loi exponentielle, car on sait que si \(Y\hookrightarrow\mathcal{E}(\lambda)\), alors \( X= \displaystyle \sqrt{2Y\sigma^2\lambda} \) suit la loi de Rayleigh de paramètre \(\sigma\).
Ainsi, \( \displaystyle E(X^2)= E( (\sqrt{2Y\sigma^2\lambda})^2) =2 E(Y) \lambda\sigma^2=2 \frac{1}{\lambda}\lambda\sigma^2 =2\sigma^2\)
Donc, d’après la formule de Köning-Huygens, \( V(X)=E(X^2)-E(X)^2=2\sigma^2-\sigma^2\frac{\pi}{2}= \sigma^2(\frac{4-\pi}{2})\)
Conclusion
Il est plus probable que cette loi tombe dans un sujet type EDHEC/EML que dans un sujet top 3. Mais ce n’est pas impossible non plus dans la mesure où elle est un cas particulier de la loi de Weibull qui est déjà tombé en 2010 (Maths 2 appli). Attention, il est inutile d’apprendre ces résultats par cœur, mais il est intéressant de savoir reproduire les calculs !
Pour t’entraîner sur cette loi, tu peux t’entraîner sur ces sujets (maths appliquées) :
- Maths EMLYON 2006 et 2012
- Maths EDHEC 2018 et 2024
- Oral HEC 2022 (sujet E1 et E5)
N’hésite pas à consulter tous nos articles en mathématiques et notre méga-répertoire maths appliquées !