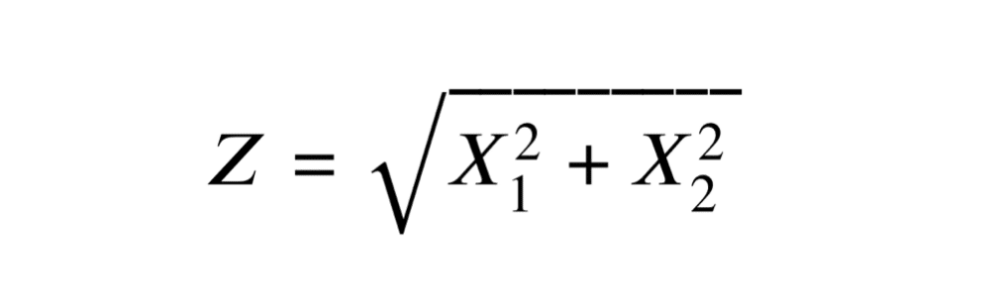En probabilités et en statistiques, il est essentiel de comprendre le lien entre différentes distributions pour modéliser des phénomènes variés et aborder avec succès des problématiques complexes. Cet article explore les connexions entre la loi normale, la loi de Rayleigh et la loi du \(\chi^2\), fondamentales dans de nombreux domaines, y compris en économie, et souligne leur importance dans la modélisation statistique. Parmi ces trois lois, il n’y a que la loi normale qui est au programme d’ECG. Cependant, il est fréquent de retrouver la loi du Khi 2 et la loi de Rayleigh dans les épreuves parisiennes. Ainsi, les propriétés que nous allons étudier te permettront d’enrichir ta préparation à l’épreuve de Maths II et aux oraux de mathématiques, offrant une perspective plus large et une compréhension approfondie des outils statistiques.
La loi de Rayleigh
La loi de Rayleigh est une distribution de probabilité continue avec de nombreuses applications pratiques, notamment dans le domaine de l’ingénierie des signaux et des communications.
La loi de Rayleigh est également un cas particulier de la loi de Weibull.
Densité
La fonction de densité de probabilité de la loi de Rayleigh est donnée par : \( \displaystyle f(z, \sigma) = \frac{z}{\sigma^2} \exp\left(-\frac{z^2}{2\sigma^2}\right), \; \text{pour} \; z \geq 0 \).
Cette densité a la particularité d’être nulle pour les valeurs négatives de \(z\).
Fonction de répartition
La fonction de répartition est exprimée comme : \( \displaystyle F(z, \sigma) = 1 – \exp\left(-\frac{z^2}{2\sigma^2}\right), z \geq 0 \).
Cette fonction est nulle pour les valeurs négatives de \(z\).
Espérance et variance
L’espérance (ou la moyenne) de la loi de Rayleigh est calculée par : \( \displaystyle \mathbb{E}[Z] = \sigma \sqrt{\frac{\pi}{2}} \)
La variance est donnée par : \( \displaystyle V[Z] = \left(2 – \frac{\pi}{2}\right) \sigma^2 \)
Lien avec la loi normale
La loi de Rayleigh peut être intuitivement comprise comme résultant de la racine carrée de la somme des carrés de deux variables normales centrées réduites indépendantes.
Si nous prenons deux variables aléatoires \( X_1 \) et \( X_2 \), chacune distribuée normalement avec une espérance de zéro et une variance de \( \sigma^2 \) (c’est-à-dire \( X_i \sim N(0, \sigma^2) \)), alors la variable aléatoire \( Z \) définie par :
\[ Z = \sqrt{X_1^2 + X_2^2} \]
suit une loi de Rayleigh de paramètre \( \sigma \).
La loi du Khi 2
La loi du \(\chi^2\), ou khi-carré, est une distribution fondamentale en statistiques, souvent utilisée pour différents tests statistiques.
Elle prend une importance particulière dans les tests d’hypothèses et les intervalles de confiance.
Définition avec des lois normales
Une variable aléatoire \(X\) suit une loi du \(\chi^2\) avec \(k\) degrés de liberté si elle peut être exprimée comme la somme des carrés de \(k\) variables aléatoires indépendantes et normalement distribuées (de moyenne nulle et de variance unitaire).
Densité de probabilité
La densité de cette distribution est donnée par : \( \displaystyle f(x, k) = \frac{1}{2^{k/2}\Gamma(k/2)} x^{(k/2)-1} e^{-x/2}, \; \text{pour} \; x \geq 0 \) où \(\Gamma\) représente la fonction gamma, et \(k\) est le nombre de degrés de liberté.
Espérance et variance
Les propriétés de cette distribution sont bien caractérisées par ses moments. L’espérance (la moyenne) de la loi du \(\chi^2\) est égale aux degrés de liberté : \( \mathbb{E}[X] = k. \)
La variance est le double des degrés de liberté : \( V[X] = 2k \)
La loi normale
Rappelons que la loi normale est caractérisée par sa densité de probabilité en forme de cloche. Elle est définie mathématiquement par deux paramètres essentiels : l’espérance \( \mu \) et la variance \( \sigma^2 \)
Ces paramètres sont les indicateurs clés de la localisation et de l’étalement de la distribution, respectivement. Voici une densité d’une variable aléatoire suivant une telle loi :
\[ \displaystyle f(x, \mu, \sigma^2) = \frac{1}{\sigma\sqrt{2\pi}} e^{\displaystyle -\frac{(x-\mu)^2}{2\sigma^2}} \]
Cette distribution est symétrique autour de la moyenne et décrit de nombreux phénomènes naturels et sociaux. Lorsque \(\mu = 0\) et \(\sigma = 1\), on parle de loi normale centrée réduite.
Le lien entre les trois lois
La loi normale, la loi de Rayleigh et la loi du \(\chi^2\) sont intimement liées par la théorie des variables aléatoires et leurs transformations.
En effet, si \(X_1\) et \(X_2\) sont deux variables aléatoires indépendantes suivant une loi normale centrée réduite, la variable \(Z=\sqrt{X_1^2 + X_2^2}\) suit une loi de Rayleigh. Cette construction géométrique donne une interprétation géométrique à la loi de Rayleigh. Elle représente la distance d’un point aléatoire à l’origine dans un espace euclidien bidimensionnel, où chaque axe est régi par une loi normale.
D’autre part, la loi du \(\chi^2\) avec deux degrés de liberté est directement liée à la loi de Rayleigh. En effet, si \(Z\) suit une loi de Rayleigh, alors \(Z^2\) suit une loi du \(\chi^2\) avec deux degrés de liberté. Cette relation est une conséquence de la définition de la loi du \(\chi^2\), qui est la somme des carrés de variables normales indépendantes.
En somme, la loi normale, fondement de la théorie des probabilités, se transforme en loi du \(\chi^2\) lorsqu’on examine la somme de leurs carrés et se transforme également en loi de Rayleigh lorsqu’on s’intéresse à la racine carrée de la somme de leurs carrés. Cette trinité de distributions forme un pont mathématique essentiel qui pourrait faire l’objet d’un sujet de Maths II ou d’un oral ESCP ou HEC.
Conclusion
La loi normale, la loi de Rayleigh et la loi du \(\chi^2\) ne sont pas seulement des entités mathématiques isolées, mais elles constituent un trio interconnecté au cœur de la théorie des distributions de probabilités. Leur compréhension et leur application judicieuse sont cruciales, en particulier pour les étudiants qui se préparent aux rigoureuses épreuves parisiennes.
En maîtrisant ces distributions, tu pourras non seulement exceller dans tes examens, mais aussi acquérir une compréhension profonde des fondements statistiques nécessaires dans le domaine économique.
Pour t’entraîner sur ces lois de probabilités, tu peux réaliser les sujets (mathématiques approfondies) suivants :
Tu peux retrouver ici toutes nos autres ressources mathématiques pour approfondir ta préparation et te familiariser davantage avec ces concepts essentiels.