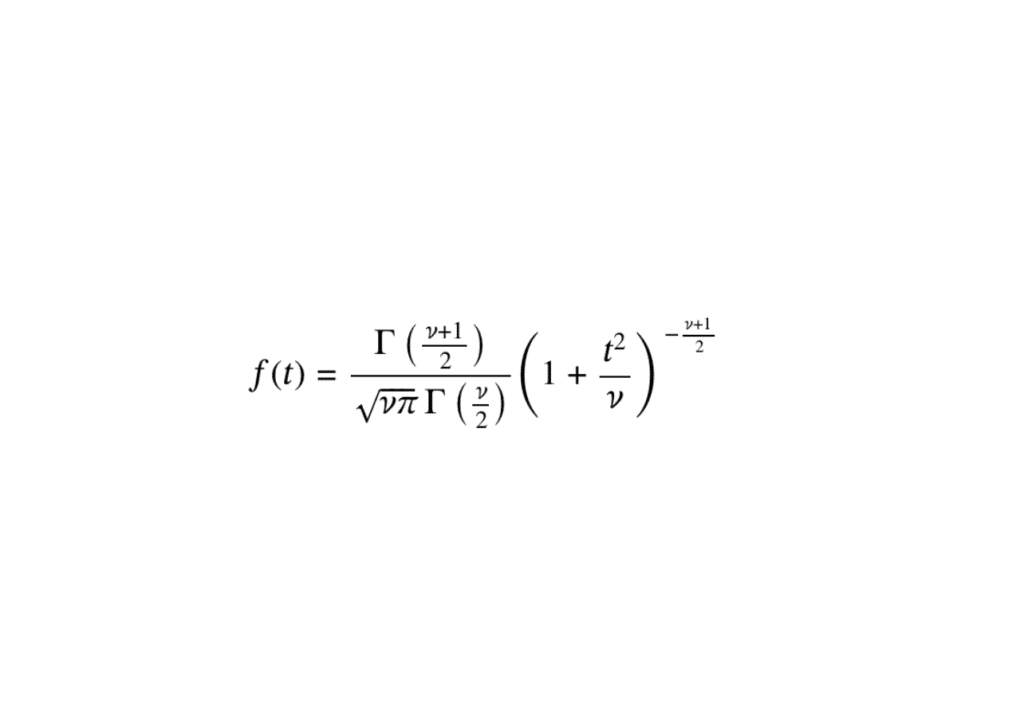On va travailler ensemble sur une loi de probabilité primordiale en statistiques : la loi de Student. Cette loi mathématique est particulièrement utile pour estimer ou étudier des échantillons. Cette loi est hors programme, mais elle pourrait très bien se retrouver dans des sujets de concours, il est donc important de maîtriser ses caractéristiques et ses diverses propriétés. C’est aussi l’occasion pour toi de revoir les méthodes des variables à densité et des lois de probabilité continues.
Présentation de la loi de Student
La loi de Student est une loi de probabilité continue à support infini. Elle correspond à la combinaison de deux lois de probabilités différentes : la loi normale centrée réduite et la loi de khi. En effet, elle est formée du quotient de ces deux lois spécifiques. Cette loi, introduite en 1908 par William Gosset, est particulièrement utilisée en statistiques, notamment pour créer des intervalles de confiance, estimer des petits échantillons ou encore des tests de Student.
Pour ta culture, William Gosset (1876-1937) était un mathématicien et statisticien britannique. C’est lorsqu’il est encore brasseur dans la brasserie Guinness qu’il développe le test de Student, aussi connu sous le nom de « test t », afin d’analyser des échantillons de petites tailles dans la production de bières. Ces tests de Student, reposant sur la loi de Student, seront ensuite popularisés grâce à la généralisation qu’en fait le biologiste et statisticien britannique Ronald Aylmer Fisher.
Définition de la loi de la Student par sa densité
On dit qu’une variable aléatoire X suit la loi de Student à \( \nu \) degrés de liberté, si et seulement si elle admet comme densité la fonction f donnée par :
\[ \displaystyle f(t) = \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi} \, \Gamma\left(\frac{\nu}{2}\right)} \left( 1 + \frac{t^2}{\nu} \right)^{-\frac{\nu+1}{2}} \]
avec \( \nu > 0 \) et \( \Gamma \) la fonction Gamma d’Euler (elle aussi hors progrmme).
Les degrés de liberté désignent un ensemble de paramètres indépendants pouvant varier librement dans un système. C’est un concept très complexe des statistiques, mais tu n’auras pas besoin de l’expliquer en mathématiques.
Vérification de la positivité
On sait déjà que la fonction \( \Gamma \) est une densité. Donc : \( \displaystyle \forall t \in \mathbb{R}, \; \gamma(t) > 0. \)
Or, on a aussi \( \nu > 0 \), donc \( \sqrt{\nu\pi} > 0 \) et comme \(\displaystyle 1 + \frac{t^2}{\nu} > 0\), alors \(\displaystyle (1 + \frac{t^2}{\nu})^{-\frac{\nu+1}{2}}\) est toujours strictement positive.
Ainsi, comme somme de termes positifs, on a donc bien pour tout \( t \in \mathbb{R}, f(t) \geq 0 \)
La fonction f est positive sur \( \mathbb{R} \).
Continuité de la fonction
Pour la continuité, on connaît déjà la fonction \( \Gamma \) (comme densité). Donc : \( \displaystyle \frac{\Gamma\left( \frac{\nu+1}{2} \right)}{\sqrt{\nu \pi}} \) est continue sur \( \mathbb{R} \).
Pour la deuxième partie de la fonction, on doit passer à l’exponentielle. En effet, on a par définition que pour tout \( a > 0 \) \( a^x = \exp(x \ln a) \). Or, comme on sait déjà que \( \displaystyle 1 + \frac{t^2}{\nu} > 0\). On peut alors écrire que :
\[ \left( 1 + \frac{t^2}{\nu} \right)^{-\frac{\nu + 1}{2}} = \exp\left( -\frac{\nu + 1}{2} \ln\left(1 + \frac{t^2}{\nu}\right) \right). \]
Or, la fonction exponentielle est continue sur \( \mathbb{R} \) ; donc comme produits de fonctions continues sur \( \mathbb{R} \), on peut en conclure que la fonction f est continue sur \( \mathbb{R} \).
Vérification que l’intégrale de f(t) sur \( \mathbb{R} \) est égale à 1
On remarque tout d’abord que la fonction \( f(t) \) est paire, car elle ne dépend que de \( t^2 \). Par parité de la fonction, on a donc :
\[ \displaystyle \int_{-\infty}^{+\infty} f(t) \, dt = 2 \int_{0}^{+\infty} f(t) \, dt \]
On pose alors : \( \displaystyle u = 1 + \frac{t^2}{\nu} \) d’où \( \displaystyle t = \sqrt{\nu (u – 1)} \)
En dérivant, on a alors que \( \displaystyle dt = \frac{\sqrt{\nu}}{2 \sqrt{u – 1}} \, du \)
En effectuant les changements bornes, on obtient donc que :
\[ \int_{0}^{+\infty} f(t) \, dt = \frac{\Gamma\left(\frac{\nu + 1}{2}\right)}{\sqrt{\nu \pi} \Gamma\left(\frac{\nu}{2}\right)} \int_{1}^{+\infty} u^{-\frac{\nu + 1}{2}} \cdot \frac{\sqrt{\nu}}{2 \sqrt{u – 1}} \, du. \]
Après calculs, à l’aide des fonctions connues Bêta et Gamma, on a :
\[ \int_{0}^{+\infty} f(t) \, dt = \frac{\Gamma\left(\frac{\nu + 1}{2}\right)}{\Gamma\left(\frac{\nu}{2}\right)} \cdot \frac{\Gamma\left(\frac{\nu}{2}\right)}{\Gamma\left(\frac{\nu + 1}{2}\right)} = \frac{1}{2} \]
Or, nous avons vu que \( \displaystyle \int_{-\infty}^{+\infty} f(t) \, dt = 2 \int_{0}^{+\infty} f(t) \, dt \) Donc, on peut en conclure que :
\[ \displaystyle \int_{-\infty}^{+\infty} f(t) \, dt = 1. \]
On a ainsi prouvé que f est une fonction de densité.
Si tu souhaites en apprendre davantage sur les lois de probabilité continues (et hors programme). N’hésite pas à jeter un œil à cet article sur la loi de Laplace.
Fonction de répartition de la loi de Student
Contrairement aux autres lois, il est difficile d’exprimer la fonction de répartition de la loi de Student de façon simple. Ici, on va donc simplement rappeler la définition de la fonction de répartition.
La fonction de répartition \( F(t) = P(X \leq t) \) de la loi de Student est donc définie par :
\[ \displaystyle \forall t \in \mathbb{R}, \quad F(t) = \int_{-\infty}^{t} f(x) \, dx \]
Autre expression de la loi de Student
Il existe une autre expression de la loi de Student, s’appuyant sur deux lois différentes (la loi normale centrée réduite et la loi du khi deux). En effet, par définition, si une variable aléatoire (ici, la variable S) peut s’écrire de la façon suivante, alors elle suit une loi de Student :
\( {\displaystyle S={\frac {Z}{\sqrt {U/k}}}} \)
avec \( Z \) une variable aléatoire suivant la loi normale centrée réduite \( N(0, 1) \) et \( U \) suit une loi \( \chi^2 \) (loi du khi deux) avec \( k \) degrés de liberté.
De même, on peut remarquer que pour \( \nu = 1 \), la densité de la loi de Student est la même que la densité de la loi de Cauchy. Ainsi pour \( \nu = 1 \), une variable suivant la loi de Student suit en réalité la loi de Cauchy.
Espérance et variance de la loi de Student
Calcul de l’espérance
À partir de ces deux façons d’exprimer la loi de Student, on peut alors facilement trouver l’espérance d’une variable suivant la loi de Student grâce à celle de la loi normale centrée réduite et aux propriétés de la loi de Cauchy.
D’une part, la loi de Cauchy n’admet pas d’espérance ni de variance. Donc, pour \( \nu = 1 \), l’espérance de la loi de Student ne peut pas être définie.
Ensuite, comme \( {\displaystyle S={\frac {Z}{\sqrt {U/ \nu}}}} \), on a alors :
\[ \displaystyle E(S) = E\left( \frac{Z}{\sqrt{U / \nu}} \right) \]
Comme \( Z \) et \( U \) sont indépendantes et que ces deux variables sont des variables connues admettant respectivement une espérance, on peut écrire que :
\[ \displaystyle E(S) = E(Z) \cdot E\left( \frac{1}{\sqrt{U / \nu}} \right) \]
Or, \( Z \) suit la loi normale centrée réduite, donc \( \displaystyle E(Z) = 0 \).
On peut donc conclure que pour \( \nu > 1 \), l’espérance de la loi de Student est nulle.
Calcul de la variance
Par un raisonnement similaire à celui du calcul de l’espérance, on en déduit que la variance ne peut pas être définie pour \( \nu = 1 \) et pour \( \nu = 2 \) d’après les propriétés de la loi de Cauchy.
À partir des propriétés de l’autre expression de la loi de Student, on peut en conclure que pour une variable \( S \) suivant la loi de Student, on a alors :
\[ \text{Pour } \nu > 2, \quad V(S) = \frac{\nu}{\nu – 2} \]
Représentation graphique de la loi de Student (Python)
Les sujets de concours faisant de plus en plus intervenir des exercices avec du Python, il peut être utile de maîtriser la loi de Student aussi dans ce langage, en particulier sa représentation graphique.
Voici le code Python qui permet d’écrire la densité d’une variable suivant la loi de Student (que tu connais désormais) :
Remarque : Inutile de connaître ce code Python par cœur, mais tu peux essayer de le comprendre au cas où tu devrais compléter des codes similaires dans un sujet de concours. Tu peux par ailleurs retrouver ici tous nos autres articles dédiés au langage Python.
Annales où retrouver la loi de Student
Cette loi est d’autant plus utile à travailler qu’elle est déjà tombée aux concours de maths approfondies, notamment dans le problème du sujet Écricome de 2005.
Je te recommande fortement de faire ces annales, car elles mettent en jeu de nombreuses notions précises, y compris la loi de Cauchy.
Ici, tu peux retrouver la correction de ce sujet Écricome.
Conclusion
Tu connais maintenant tout sur la loi de Student ! Tu es désormais capable de donner sa densité, son espérance, sa variance et de calculer sa fonction de répartition et sa représentation graphique sur Python. J’espère que cet article t’a plu.
Tu peux retrouver ici toutes nos autres ressources mathématiques et continuer à t’exercer sur d’autres annales grâce à notre méga-répertoire.