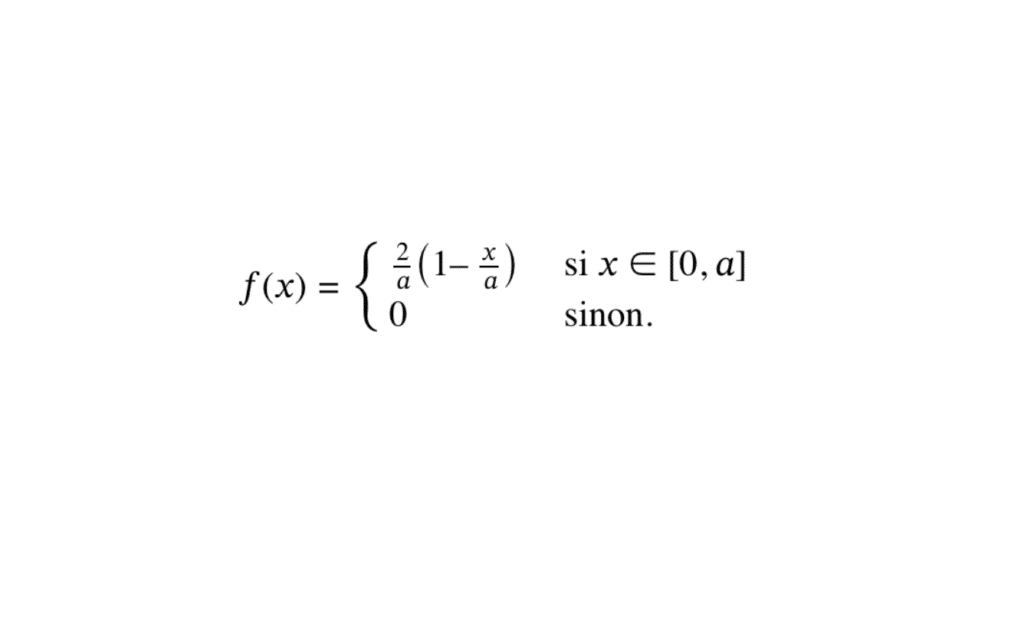On va travailler ensemble sur une loi de probabilité très particulière : la loi de Xenakis. Cette loi mathématique a contribué à l’apparition d’un nouveau genre musical : la musique stochastique. La loi de Xenakis (hors programme) pourrait très bien se retrouver dans des sujets de concours. Il est donc important de maîtriser ses caractéristiques et ses diverses propriétés. C’est aussi l’occasion pour toi de revoir les méthodes des variables à densité et des lois de probabilité continues.
Présentation de la loi de Xenakis
La loi de Xenakis est une loi de probabilité continue à support fini. Elle se distingue des autres lois par sa fonction de densité, mais surtout par l’usage musical que l’on en a fait. En effet, cette loi, introduite et utilisée par Iannis Xenakis, permet de représenter les variations de hauteur ainsi que les durées de notes musicales. Elle a contribué à la création de la musique stochastique, autrement dit une musique probabiliste qui, par conséquent, était prévisible (bien qu’aléatoire).
Pour ta culture, Iannis Xenakis (1922-2001) était un compositeur et architecte franco-grec de renom. Il est particulièrement connu pour ses travaux sur les modèles probabilistes qui ont fortement influencé la musique contemporaine. En effet, Xenakis, en intégrant des principes mathématiques et de physique dans ses compositions musicales, est ainsi devenu l’un des pionniers de la musique stochastique.
Définition de la loi de Xenakis
La loi de Xenakis est d’abord la loi d’une variable aléatoire positive.
Soit \( a \in \mathbb{R}^+ \), on dit qu’une variable aléatoire X suit la loi de Xenakis sur un intervalle général \( [0, a] \) , si elle admet comme densité la fonction f donnée par :
\( f(x) = \begin{cases} \frac{2}{a} \left(1 – \frac{x}{a}\right) & \text{si } x \in [0, a] \\ 0 & \text{sinon.} \end{cases} \)
On va vérifier que la fonction f est bien une densité de probabilité, avec les trois points essentiels (une question de probabilité très récurrente aux concours).
Vérification de la positivité
Pour \( x \notin [0, a] \), \( f(x) = 0 \), donc f est positive sur \( x \notin [0, a] \).
Sur \( [0, a] \), on s’intéresse à la fonction \( \displaystyle 1 – \frac{x}{a} \).
Cette fonction est décroissante sur l’intervalle \( [0, a] \). Or, pour \( x = 0 \), \[ f(0) = \frac{2}{a} (1 – 0) = \frac{2}{a} > 0. \] et pour \( x = a \), \[ f(a) = \frac{2}{a} (1 – 1) = 0. \]
Donc, la fonction f est positive pour \( x \in [0, a[ \) et s’annule en \( a \).
On a donc bien pour tout \( x \in \mathbb{R}, f(x) \geq 0 \). La fonction f est positive sur \( \mathbb{R} \).
Continuité de la fonction
On prouve aisément que la fonction est continue sur \( \displaystyle ]0, a[ \), car il s’agit d’une fonction polynomiale et sur \( \displaystyle ]-\infty, 0[ \cap ]a, +\infty-[ \) comme fonction constante.
De plus, on trouve aussi que \[ \lim_{x \to 0} f(x) = \frac{a}{2} = f(0), \] et \[ \lim_{x \to a} f(x) = 0 = f(a), \]
Donc, la fonction f est continue sur \( \mathbb{R} \).
Vérification que l’intégrale de f(x) sur \( \mathbb{R} \) est égale à 1
On a tout d’abord \[ \int_{-\infty}^{+\infty} f(x) \, dx = \int_{0}^{a} f(x) \, dx\] car f est nulle en dehors de l’intervalle \( [0, a] \).
Or, \[ \int_{0}^{a} f(x) \, dx = \int_{0}^{a} \frac{a}{2} \left(1 – \frac{a}{x}\right) \, dx \] \[ = \frac{2}{a} \int_{0}^{a} \left(1 – \frac{x}{a}\right) \, dx \] \[ = \frac{2}{a} \left( \int_{0}^{a} 1 \, dx – \int_{0}^{a} \frac{x}{a} \, dx \right) \]
En effectuant les calculs sur chaque intégrale, on a alors :
\[ \int_{0}^{a} 1 \ = a \] et \[ \int_{0}^{a} \frac{x}{a} \, dx =\frac{a}{2} \]
En incorporant ces résultats à l’intégrale de départ, on trouve donc bien que :
\[ \int_{0}^{a} f(x) \, dx = \frac{a}{2} \left(a – \frac{2}{a}\right) = 1 \]
On a ainsi prouvé que f est une fonction de densité.
Si tu souhaites en apprendre davantage sur les lois de probabilité continues (et hors programme), n’hésite pas à jeter un œil à cet article sur la loi de Laplace !
Fonction de répartition de la loi de Xenakis
La fonction de répartition F(x) d’une variable aléatoire X suivant la loi de Xenakis (qui, pour rappel, correspond à la probabilité que X prenne une valeur inférieure ou égale à x) est définie par :
\( F(x) = \begin{cases} 0 & \text{si } x < 0 \\ \frac{2x}{a} – \frac{x^2}{a^2} & \text{si } 0 \leq x \leq a \\ 1 & \text{si } x > a \end{cases} \)
Astuce sur la loi de Xenakis en lien avec la loi uniforme
Si on pose une variable aléatoire réelle \( Y = a\left(1 – \sqrt{1 – X}\right) \) avec \( X \) une variable aléatoire qui suit une loi uniforme sur \([0; 1]\), alors on peut montrer que la variable \( Y \) suit en réalité une loi de Xenakis de paramètre \( a \).
Espérance et variance de la loi de Xenakis
Une variable suivant la loi de Xenakis admet toujours une espérance, car elle est continue à support fini. Elle admet alors toujours une variance, puisqu’elle possède une espérance, et que l’intégrale donnée par \( \mathbb{E}[X^2] \) est convergente.
Calcul de l’espérance
Pour trouver l’espérance d’une variable aléatoire suivant la loi de Xenakis, on a :
\(
\displaystyle \mathbb{E}[X] = \int_{-\infty}^{+\infty} x f(x) \, dx = \int_{0}^{a} x f(x) \, dx
\)
\(
\displaystyle \mathbb{E}[X] = \int_{0}^{a} x\left(\frac{a}{2}\left(1 – \displaystyle\frac{a}{x}\right)\right)dx = \displaystyle \frac{a}{2}\left(\int_{0}^{a} x \, dx – \frac{1}{a}\int_{0}^{a} x^2 \, dx\right)
\)
Après calculs, on trouve alors que l’espérance d’une variable suivant la loi de Xenakis est égale à :
\[
\mathbb{E}[X] = \frac{2}{a} \left( \frac{a^2}{3} – \frac{1}{a} \cdot \frac{a^3}{3} \right) = \frac{a}{3}
\]
L’espérance de la loi de Xenakis est donc \( \displaystyle \mathbb{E}[X] = \frac{a}{3} \)
Calcul de la variance
Pour trouver la variance d’une variable aléatoire suivant la loi de Xenakis, on utilise la formule (bien connue) de König \( \displaystyle \text{V}(X) = \mathbb{E}[X^2] – (\mathbb{E}[X])^2 \). On sait déjà que l’espérance est égale à \( \displaystyle \mathbb{E}[X] = \frac{a}{3} \).
On commence par calculer la valeur de \( \displaystyle \mathbb{E}[X^2] \) :
\( \displaystyle \mathbb{E}[X^2] = \int_{0}^{a} x^2 f(x) \, dx = \int_{0}^{a} x^2 \left(\frac{2}{a}\left(1 – \frac{x}{a}\right)\right) \, dx \)
\( \displaystyle \mathbb{E}[X^2] = \frac{2}{a} \left( \frac{a^3}{3} – \frac{1}{a} \cdot \frac{a^4}{4} \right) = \frac{a^2}{6} \)
Par la formule de König, on trouve alors :
\( \displaystyle V(X) = \mathbb{E}[X^2] – (\mathbb{E}[X])^2 = \frac{a^2}{6} – \frac{a^2}{9} \)
La variance de la loi de Xenakis est donc \( \displaystyle \text{V}(X) = \frac{a^2}{18} \)
Représentation graphique de la loi de Xenakis (Python)
Les sujets de concours faisant de plus en plus intervenir des exercices avec du Python, il peut être utile de maîtriser la loi de Xenakis aussi dans ce langage, en particulier sa représentation graphique.
Voici tout d’abord le code Python qui permet d’écrire la densité d’une variable suivant la loi de Xenakis (que tu connais désormais) :
Mais il est aussi intéressant de savoir représenter graphiquement la fonction de répartition d’une variable suivant la loi de Xenakis, et on peut aussi le faire dans le langage Python :
Remarque : inutile de connaître ces deux codes Python par cœur, mais tu peux essayer de les comprendre au cas où il te serait demandé de compléter des codes similaires dans un sujet de concours. Tu peux par ailleurs retrouver ici tous nos autres articles consacrés au langage Python.
Conclusion
Te voilà au point sur la loi de Xenakis. Tu peux maintenant donner sa densité, son espérance, sa variance et calculer sa fonction de répartition et sa représentation graphique sur Python.
Tu peux retrouver ici toutes nos autres ressources mathématiques et continuer à t’exercer sur d’autres annales grâce à notre méga-répertoire.