La loi de Zipf est une loi de probabilité discrète hors programme, mais facilement analysable avec les outils mis à disposition d’un élève de deuxième année bien entraîné ! Dans cet article, il sera donc question de la définition de cette loi, de ses propriétés intéressantes qui pourraient faire l’objet de questions sur un sujet de type EMLyon, ainsi que la modélisation Python de cette loi.
Introduction au concept de la loi de Zipf
La loi de Zipf est une loi empirique qui décrit la fréquence d’apparition des mots dans un corpus de texte. Elle stipule que, dans un grand ensemble de données textuelles, la fréquence d’un mot est inversement proportionnelle à son rang dans la liste des mots triés par fréquence.
Cette loi est observée dans de nombreux contextes et est utilisée dans divers domaines, notamment en linguistique, en informatique et en économie.
En ce sens, la loi de Zipf a diverses applications concrètes. Par exemple, elle peut être utilisée pour optimiser les moteurs de recherche ou pour analyser les tendances linguistiques. Regardons dès lors la définition mathématique de cette loi.
Définition
La loi de Zipf peut être formulée mathématiquement comme suit :
Soit \( f \) la fréquence d’un mot, et \( k \) son rang lorsque les mots sont classés par fréquence décroissante.
La relation entre la fréquence \( f \) et le rang \( k \) est donnée par :
\[
P(X=k) = \frac{1}{\zeta(s)} \cdot \frac{1}{k^s}
\]
où :
\(\zeta(s)\) est la fonction zêta de Riemann, définie par \(\zeta(s) = \sum_{i=1}^{\infty} \frac{1}{i^s}\).
\( s \) est un paramètre qui ajuste la distribution (qui doit être supérieur à 1 par un critère de convergence des séries de Riemann).
Tu peux également noter que par définition de \(k\), on a \(X(\Omega) = \mathbb{N^*}\)
Tu pourras aisément vérifier que \(X\) vérifie bien une loi de probabilité discrète en notant que tous les \(P(X=k)\) sont positifs et que \(\sum_{i=1}^{k} P(X=k) = 1\). En effet, le réel \(\frac{1}{\zeta(s)}\) est appelé « coefficient de normalisation » en ce qu’il permet que \(\sum_{i=1}^{k} P(X=k) = 1\) et donc que l’on définisse bien une loi de probabilité discrète.
Propriétés
Fonction de répartition
La fonction de répartition \( F(k) \) pour la loi de Zipf est la somme des probabilités jusqu’au rang \( k \) :
\[
F(k) = P(X \leq k) = \sum_{i=1}^{k} P(X = i) = \sum_{i=1}^{k} \frac{1}{\zeta(s)} \cdot \frac{1}{i^s}
\]
Espérance
L’espérance \( E(X) \) est calculée comme suit :
\[
E(X) = \sum_{k=1}^{\infty} k \cdot P(X=k) = \sum_{k=1}^{\infty} k \cdot \frac{1}{\zeta(s)} \cdot \frac{1}{k^s} = \frac{1}{\zeta(s)} \sum_{k=1}^{\infty} \frac{1}{k^{s-1}} = \frac{\zeta(s-1)}{\zeta(s)}
\]
Attention : pour que cette somme converge, il faut que \( s – 1 > 1 \) (voir ton cours sur la convergence des séries de Riemann), c’est-à-dire \( s > 2 \).
Variance
La variance \( \text{Var}(X) \) est calculée en utilisant l’espérance de \( X^2 \) par application de la formule de Koenig-Huygens :
\[
\text{Var}(X) = E(X^2) – (E(X))^2
\]
Pour calculer \( E(X^2) \) :
\[
E(X^2) = \sum_{k=1}^{\infty} k^2 \cdot P(X = k) = \sum_{k=1}^{\infty} k^2 \cdot \frac{1}{\zeta(s)} \cdot \frac{1}{k^s} = \frac{1}{\zeta(s)} \sum_{k=1}^{\infty} \frac{1}{k^{s-2}} = \frac{\zeta(s-2)}{\zeta(s)}
\]
Pour que cette somme converge, il faut que \( s – 2 > 1 \), c’est-à-dire \( s > 3 \). Et il ne reste plus qu’à simplifier l’expression obtenue pour déterminer la variance de la loi de Zipf.
Généralisation (moments d’ordre k)
Le moment d’ordre \(k\) de \(X\) est défini par :
\[
\mathbb{E}[X^k] = \sum_{n=1}^{\infty} n^k \cdot P(X = n)
= \sum_{n=1}^{\infty} n^k \cdot \frac{1}{\zeta(s)} \cdot \frac{1}{n^s}
= \frac{1}{\zeta(s)} \sum_{n=1}^{\infty} \frac{1}{n^{s-k}} =\frac{\zeta{(s-k)}}{\zeta(s)}
\]
Attention, il convient ici de noter que la série converge si et seulement si \(s – k > 1\), donc que l’existence du moment d’ordre \(k\) est conditionné à cette condition.
Généralisation de la loi de Zipf (loi de Zipf-Mandelbrot)
La loi de Zipf peut être généralisée à l’aide de la loi de Zipf-Mandelbrot, qui introduit un paramètre de décalage noté \(q\). Cette loi est définie par :
\[
P(X = k) = \frac{1}{C} \cdot \frac{1}{(k + q)^s}
\]
où :
\(s > 1\) est un paramètre de pente qui est d’ailleurs également présent dans la loi classique de Zipf
\(q \geq 0\) est un paramètre de décalage (propre à la loi de Zipf-Mandelbrot)
\(C = \sum_{n=1}^{\infty} \frac{1}{(n + q)^s}\) est une constante de normalisation qui assure que la somme des \(P(X=k)\) vaut bien 1.
On constate ainsi aisément que lorsque \(q = 0\), on retrouve la loi de Zipf standard :
\[
P(X = k) = \frac{1}{\zeta(s)} \cdot \frac{1}{k^s}
\]
Concrètement, l’ajout du paramètre \(q\) permet de modéliser une décroissance moins abrupte des probabilités pour les petits rangs \(k\). Cette généralisation rend la loi plus flexible et mieux adaptée à la modélisation de distributions réelles. Tu verras, à l’issue de la troisième partie de cet article, une comparaison graphique entre des réalisations de ces deux lois pour mieux comprendre son intérêt !
Simulation Python de la loi
Pour mieux comprendre l’articulation entre la loi de Zipf et sa généralisation, je te propose de réaliser un script Python qui permet de simuler sur un même graphique les deux lois pour un paramètre \(s = 2.3\) (ce paramètre a été décidé relativement arbitrairement, il faut toutefois \(s>1\) pour assurer l’existence de la loi) commun aux deux lois et un paramètre \(q=5\) pour la généralisation de la loi de Zipf.
Étant donné que l’on cherche des réalisations empiriques, posons arbitrairement que l’on réalisera 10 000 réalisations des deux lois.
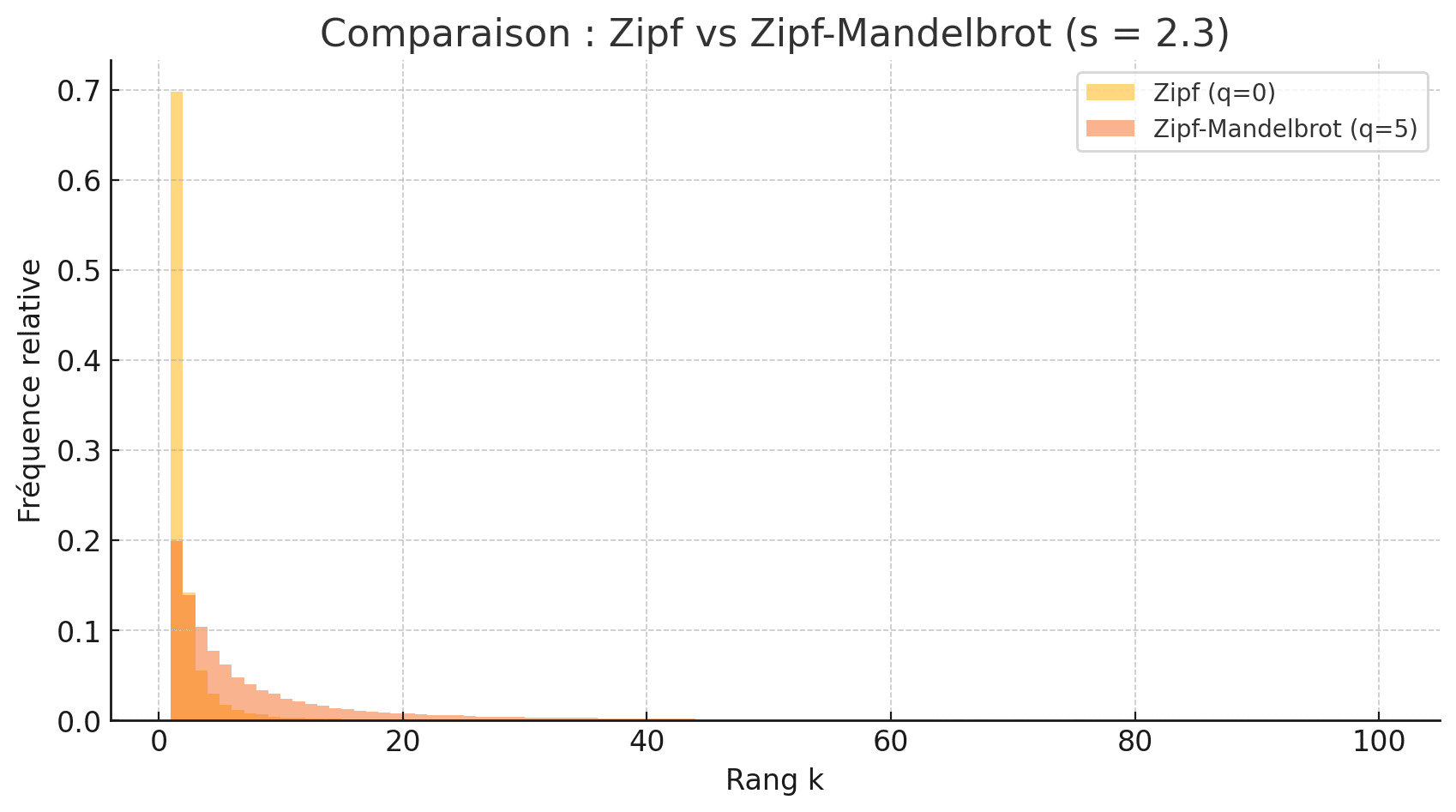
Voici une proposition de code qui permet d’y parvenir ainsi que le graphique que l’on obtient :
Voici ce qui est retourné par ce code :
À l’évidence, les lignes de code proposées plus haut ne sont qu’une proposition de corrigé et il est possible d’arriver à un résultat semblable par des développements différents.
Ainsi, tu remarques que l’ajout du paramètre \(q\) dans la généralisation de la loi de Zipf permet de modéliser une décroissance plus faible de la densité (comparé à la situation \(q=0\)).
Conclusion
En définitive, la loi de Zipf est une loi empirique fondamentale dont l’étude pourrait faire l’objet d’une partie de sujet de concours. Comme cette notion n’est encore jamais tombée au concours, cela en ferait une excellente candidate pour une partie de sujet type EMLyon ou EDHEC.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !