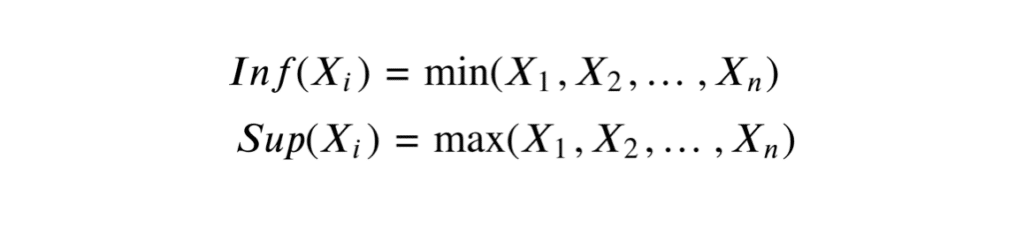Dans le domaine des mathématiques, et plus précisément en probabilités, l’étude des variables extrêmes joue un rôle crucial, surtout dans les applications économiques et financières. Les variables extrêmes, à savoir le minimum (Inf\(X_i\)) et le maximum (Sup\(X_i\)) d’une série de variables aléatoires, permettent d’analyser les risques et de prévoir les événements rares. Cet article explore les concepts fondamentaux des lois des variables extrêmes, illustrés par des exemples et des démonstrations à connaître.
Concept de base
Pour une série de variables aléatoires \(X_1, X_2, …, X_n\), le minimum et le maximum sont définis respectivement comme suit :
– \(Y_{min} = Inf(X_i) = \min(X_1, X_2, …, X_n)\)
– \(Y_{max} = Sup(X_i) = \max(X_1, X_2, …, X_n)\)
La distribution de ces variables extrêmes, c’est-à-dire la loi que suivent \(Y_{min}\) et \(Y_{max,}\) est essentielle pour comprendre comment les valeurs extrêmes se comportent dans un grand ensemble de données.
Pour démontrer les fonctions de répartition des variables extrêmes \(Y_{min}\) et \(Y_{max,}\) nous allons nous appuyer sur l’hypothèse fondamentale que les variables aléatoires \(X_1, X_2, …, X_n\) sont indépendantes et identiquement distribuées (i.i.d.) avec une fonction de répartition commune \(F(x).\) Cette indépendance est cruciale pour l’analyse qui suit, car elle nous permet d’appliquer le principe que la probabilité d’une intersection d’événements indépendants est le produit de leurs probabilités individuelles.
Démonstration pour le minimum
Pour la fonction de répartition de \(Y_{min} = \min(X_1, X_2, …, X_n)\), nous allons dans un premier temps chercher la probabilité que \(Y_{min}\) dépasse strictement un certain seuil \(x\), soit \(P(Y_{min} > x)\).
Cette probabilité peut être interprétée comme la probabilité que toutes les variables \(X_i\) soient strictement supérieures à \(x\). En utilisant l’indépendance des \(X_i\), nous avons : \( P(Y_{min} > x) = P(X_1 > x \cap X_2 > x \cap … \cap X_n > x) \)
Puisque les variables sont indépendantes, la probabilité conjointe de plusieurs événements est le produit de leurs probabilités individuelles : \( P(X_1 > x) \times P(X_2 > x) \times … \times P(X_n > x) \)
La probabilité qu’une variable aléatoire \(X_i\) soit strictement supérieure à \(x\) est \(1 – F(x)\), où \(F(x)\) est la fonction de répartition de \(X_i\). Donc, la probabilité que tous les \(X_i\) soit strictement supérieurs à \(x\) est \( (1 – F(x))^n. \)
La fonction de répartition de \(Y_{min,}\) notée \(F_{Y_{min}}(x)\), est le complément de cette probabilité :
\[ F_{Y_{min}}(x) = 1 – P(Y_{min} > x) = 1 – (1 – F(x))^n \]
Démonstration pour le maximum
Pour \(Y_{max} = \max(X_1, X_2, …, X_n)\), la fonction de répartition \(F_{Y_{max}}(x)\) représente la probabilité que \(Y_{max}\) soit inférieur ou égal à \(x\), soit \(P(Y_{max} \leq x)\).
Cette probabilité est équivalente à ce que toutes les variables \(X_i\) soient inférieures ou égales à \(x\). En utilisant à nouveau l’indépendance des \(X_i\) :
\[ P(Y_{max} \leq x) = P(X_1 \leq x \cap X_2 \leq x \cap … \cap X_n \leq x) = P(X_1 \leq x) \times P(X_2 \leq x) \times … \times P(X_n \leq x) \]
De plus, la probabilité qu’une variable aléatoire \(X_i\) soit inférieure ou égale à \(x\) est \(F(x)\). D’où le fait que la probabilité que toutes les \(X_i\) soit inférieures ou égales à \(x\) est \( F(x) \times F(x) \times … \times F(x) = F(x)^n \)
Par conséquent, la fonction de répartition de \(Y_{max}\) est : \( F_{Y_{max}}(x) = F(x)^n. \)
Ces démonstrations montrent comment l’indépendance des variables aléatoires permet de simplifier considérablement l’analyse des variables extrêmes. En utilisant l’indépendance pour séparer les probabilités conjointes en produits de probabilités individuelles, nous pouvons facilement dériver les fonctions de répartition pour le minimum et le maximum d’un ensemble de variables aléatoires indépendantes. Ces résultats sont fondamentaux en probabilités et statistiques et trouvent des applications dans de nombreux domaines, notamment en économie et en gestion des risques.
Validation mathématique des fonctions de répartition
Pour démontrer que \(F_{Y_{min}}(x)\) et \(F_{Y_{max}}(x)\) sont des fonctions de répartitions de variables aléatoires à densité, nous devons vérifier la continuité de ces fonctions, ainsi que leurs comportements aux limites.
Fonction de répartition de \(Y_{min}\)
La fonction de répartition de \(Y_{min}\) est définie par :
\[ F_{Y_{min}}(x) = 1 – (1 – F(x))^n \]
Pour prouver sa continuité, remarquons que \(F(x)\) est continue en tant que fonction de répartition d’une variable aléatoire à densité. Ainsi, \(1 – F(x)\) est également continue, tout comme \((1 – F(x))^n\), et par conséquent \(1 – (1 – F(x))^n\) l’est aussi.
Examinons ses limites :
– Lorsque \(x \to -\infty\), \(F(x) \to 0\), donc \(F_{Y_{min}}(x) \to 1 – (1 – 0)^n = 0\).
– Lorsque \(x \to +\infty\), \(F(x) \to 1\), donc \(F_{Y_{min}}(x) \to 1 – (1 – 1)^n = 1\).
Fonction de répartition de \(Y_{max}\)
La fonction de répartition de \(Y_{max}\) est donnée par :
\[ F_{Y_{max}}(x) = F(x)^n \]
Sa continuité découle directement de celle de \(F(x)\), étant donné que l’élévation à la puissance \(n\) d’une fonction continue reste continue.
Pour les limites :
– Quand \(x \to -\infty\), \(F(x) \to 0\), d’où \(F_{Y_{max}}(x) \to 0^n = 0\).
– Quand \(x \to +\infty\), \(F(x) \to 1\), par conséquent \(F_{Y_{max}}(x) \to 1^n = 1\).
Ces démonstrations montrent que \(F_{Y_{min}}(x)\) et \(F_{Y_{max}}(x)\) remplissent bien les conditions requises pour être des fonctions de répartition de variables aléatoires à densité : elles sont continues sur \(\mathbb{R}\) et leurs limites sont conformes à celles d’une fonction de répartition, tendant vers 0 lorsque \(x\) tend vers \(-\infty\) et vers 1 lorsque \(x\) tend vers \(+\infty\).
Exercice avec des lois exponentielles
Supposons que nous avons \(n\) variables aléatoires indépendantes et identiquement distribuées \(X_1, X_2, …, X_n\), chacune suivant une loi exponentielle de paramètre \(\lambda > 0\). La fonction de répartition d’une variable aléatoire \(X\) suivant une loi exponentielle est \(F(x) = 1 – e^{-\lambda x}\) pour \(x \geq 0\).
Exprimons la fonction de répartition de \(Y_{min}\) et \(Y_{max}\) en utilisant \(F(x)\) et \(n\), spécifiquement pour des variables aléatoires suivant une loi exponentielle.
Pour des variables aléatoires indépendantes suivant une loi exponentielle, la fonction de répartition de \(Y_{min}\) est :
\[ F_{Y_{min}}(x) = 1 – (1 – F(x))^n = 1 – (e^{-\lambda x})^n = 1 – e^{-n\lambda x} \]
De même, la fonction de répartition de \(Y_{max}\) est :
\[ F_{Y_{max}}(x) = (F(x))^n = (1 – e^{-\lambda x})^n \]
Conclusion
La compréhension des lois des variables extrêmes est essentielle pour les étudiants préparant leurs concours, car c’est un thème récurrent, que ce soit dans les épreuves parisiennes ou bien dans les sujets EML, EDHEC et Ecricome. Ainsi, bien que cette notion soit hors programme, une compréhension approfondie de cette dernière te permettra de compléter tes connaissances en probabilités et de te préparer pour certaines épreuves, comme le Maths II.
Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants :
- Maths II 2022 (mathématiques approfondies)
- Maths EDHEC 2020 (mathématiques approfondies)
- Maths EML 2016 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !