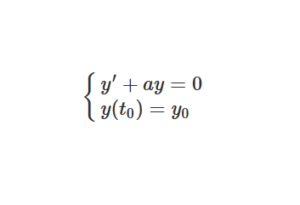Voilà l’analyse de l’épreuve de maths 2 approfondies HEC ESCP 2024, une épreuve phare du concours de la BCE pour les maths approfondies. Souvent centrée autour des probabilités, cette épreuve compte pour de nombreuses écoles ! Si les maths 2 appro HEC ESCP peuvent être une épreuve qui fait peur, pas d’inquiétude : nul besoin de finir le sujet pour avoir une très bonne note ! (Encore heureux !!)
On t’invite tout d’abord à découvrir le sujet de Maths II approfondies HEC ESCP 2024.
Rejoins nous en live tous les soirs de concours dans notre live inside concours BCE pour un débrief rapide des maths II approfondies HEC ESCP .
Analyse des maths 2 approfondies HEC ESCP 2024
Le sujet de maths 2 approfondies 2024 comporte 3 parties et porte presque exclusivement sur les probabilités et notamment sur la loi exponentielle.
Partie I : échantillon de variables aléatoires
La première question nous fait travailler sur les variables extrêmes et il faut trouver la densité d’une variable aléatoire qui correspond au maximum des \(X_i\). Il faut utiliser le fait que la fonction de répartition d’une telle variable vaut\(F^n,\) il faut ensuite dériver cette fonction. La 1) b) demande d’appliquer un raisonnement analogue mais cette fois pour le minimum des \(X_i.\)
La question 2) nous demande de montrer que \(Y{i,x}\) suit une loi de Bernoulli. Cela peut se faire en observant le support de cette variable, le paramètre vaut ici \(F(x).\) La 2) nécessite de la rigueur en travail avec des événements \(\omega,\) cela nous permet dans le sens direct et dans le sens indirect de montrer l’égalité. Pour montrer l’égalité de la 2) c), il faut utiliser le fait que \( \displaystyle \sum_{i=1}^n Y{(i,x)} \) suit une loi binomiale. Cela nous permet de passer aux probabilités à partir de la 2) b) et conclure.
La question 3) a) peut se faire par calcul en partant de la définition des objets introduits. La 3) b) consiste à utiliser le résultat de la 3) a) en remarquant une somme télescopique. La 3) c) est une question de synthèse qui nous demande de remarque le lien entre l’expression de la 3) b) et la 2) c).
Pour montrer les égalités d’événements de la 4) il faut procéder par inclusion en montrant qu’un événement implique l’autre. Que ce soit dans la 4) a) et dans la 4) b) il fallait passer aux probabilités dans les inclusions que nous venons de montrer puis appliquer le théorème des gendarmes ce qui nous permet de trouver les limites attendues.
La question 5) nécessite dans un premier temps d’utiliser la stricte positivité de \(f\) sur \([a,b]\), le fait qu’elle soit nulle pour tout autre point et le fait que \(f\) est la dérivée de \(F.\) Les convergences s’appuient sur les résultats de limites dans la question 4).
Les questions 6) et 7) de Python nous font utiliser la bibliothèque numpy. Il fallait créer une fonction qui trie des valeurs en les insérant à leur bonne position. Ensuite en utilisant cette fonction il fallait en créer une autre qui simule \(X_{n,k}\) i.e. la k-ème plus grande valeur parmi les \(X_i.\) D’où le lien avec la fonction tri ! Il fallait ensuite programmer la fonction ech pour afficher plusieurs simulations des variables aléatoires successives.
Partie II
Dans cette deuxième partie les \(X_i\) suivent des lois exponentielles de paramètre \(\lambda.\) De nouvelles variables aléatoires sont introduites, les \(T_i\) qui suivent des lois exponentielles de paramètre \((n-i+1)\lambda\).
Il faut commencer cette partie qui se fait sur l’entier naturel \(k\) supérieur à 1 et inférieur à \(n.\) La 1) b) peut se faire en identifiant les densités. Ensuite la seconde question nécessite d’utiliser le résultat de la 8) b) ce qui nous permet d’avoir une densité de \(X_{(n,k)}\) et donc de calculer l’espérance et la variance demandée.
La question 10) se fait en plusieurs étapes. Premièrement, l’inégalité se fait un utilisant le fait que \(x\) est supérieur à \(j\) et inférieur à \(j+1.\) Il faut ensuite utiliser cette inégalité avec l’espérance que nous avons trouvée dans la 10 a). Finalement, la 10) c) demande d’utiliser le fait que \(\alpha \in [0,1],\) puis utiliser le théorème des gendarmes sur l’inégalité de la 10) b). Pour montrer la question 11), on peut partir de l’expression de la variance montrée dans la 9) pour fair un changement de variable qui nous permet de montrer une convergence vers 0. Quant à l’inégalité de la 12), l’inégalité de Markov permet de conclure. Cette égalité permet de montrer la convergence en probabilité de la 12) b).
La question 13) nous demande de reconnaître que le résultat que nous venons de montrer dans la 12) b) est celui que nous avons montré dans la question 5) b) de la première partie. La convergence de la question 14) nécessite d’utiliser le \(m\) au dénominateur de la variable aléatoire introduite. Pour montrer l’égalité suivante, on peut d’abord raisonner avec des événements puis passer aux probabilités.
Partie III : démonstration d’un théorème
Le but de cette dernière partie est de démontrer le théorème introduit en début de partie mais dans le cas \(n=2.\)
La question 15) nous fait comparer le résultat que nous offre ce théorème avec le résultat de la question 8) b). Ce résultat est davantage complet car les variables aléatoires ne suivent plus juste la même loi mais sont égales.
La question 16) introduit une nouvelle variable aléatoire discrète. Le calcul de son espérance se fait par le calcul d’une série et sa variance peut se trouver par calcul de séries en utilisant la formule de Huygens.
Pour résoudre la question 17) il suffit de réécrire la probabilité demandée à l’aide d’un produit de séries en utilisant la mutuelle indépendance des \(Z_i\) et le fait que \(U_n\) est la variable qui correspond au minimum d’un vecteur de variables aléatoires. Il faut ensuite identifier cette nouvelle loi en fonction de \(r.\) La question 18) demande d’étudier l’événement dans la probabilité pour aboutir à une expression de cette dernière.
La question 19) commence avec l’étude de variables aléatoires définit par des parties entières. Pour identifier les lois il faut utiliser que \(Z_1\) vaut \(k\) si et seulement si \(mX_1\) est supérieur à \(k\) et strictement inférieur à \(k+1,\) nous pouvons ainsi conclure en utilisant la fonction de répartition de \(X_1.\) Il faut ensuite considérer des événements \(\omega\) de l’univers pour montrer les inclusions demandées qui demanderont d’utiliser les inégalités usuelles de la partie entière. Il faut ensuite passer aux probabilités et utiliser les fonctions de répartition des lois respectives dans l’inégalité. Finalement, la 19) d) peut se faire avec le théorème des gendarmes.
Le début de la question 20) demande d’utiliser que les variables \(X_{(i)}\) ont un support non dénombrable donc la probabilité que l’une vaut l’autre est de 0. Ensuite la stricte positivités découle de leur lien avec la loi exponentielle qui a un support dans \(\mathbb{R}_+.\) Finalement, il faut travailler avec 2 cas : \(X_{(1)}\) est plus grand que \(X_{(2)}\) et le cas contraire.
On espère que cette épreuve de Maths 2 approfondies HEC ESCP 2024 s’est bien passée ! Tu pourras retrouver toute l’actualité du concours BCE 2024 sur notre rubrique Inside Concours BCE 2024.