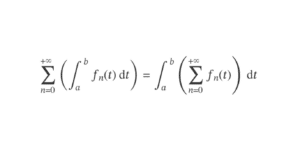La première journée des concours s’achève par la très attendue épreuve de maths approfondies emlyon 2024. Même si cette épreuve reste un grand classique pour nombre de candidats, elle n’est pas à négliger, car elle nécessite une rédaction scrupuleuse, vraiment soignée, rigoureuse et les correcteurs seront intransigeants. Retrouve dans cet article l’analyse du sujet de maths approfondies emlyon 2024.
Si tu n’as pas encore vu le sujet, tu peux le retrouver ici. Pour retrouver toutes les informations sur les concours BCE 2024, consulte notre page dédiée Inside Concours BCE 2024.
Cette année, Major Prépa t’accompagne tous les jours pendant les concours ! Retrouve le Live Inside Concours à 18h30 tout au long des concours BCE. Tu trouveras notamment une brève analyse du sujet de maths approfondies emlyon 2024.
L’analyse du sujet maths approfondies emlyon 2024
Les maths EML sont la première épreuve de maths du concours BCE. La nomenclature proposée a évoluée avec seulement deux exercices qui était longs et dont la complexité évoluait au fil des questions.
Encore cette année, les candidats ont du travailler sur un sujet particulièrement long : il fallait donc adopter une rédaction précise et efficace pour avoir le temps d’avancer le plus loin possible !
L’ensemble des questions balaie largement tous les thèmes du programme. Comme à leur habitude, les concepteurs ont proposé des questions classiques mais également des questions particulièrement discriminante en fin d’exercices !
Problème 1 : Matrices et racines de matrice
Ce premier problème nous fait travailler autour de la notion de racine carrée d’une matrice i.e. une matrice \(M\) telle que \(M^2=A.\) Ensuite, ce problème nous fait étudier le lien entre une suite et son application avec des matrices.
Partie I
Pour montrer le résultat de la question 1) il faut utiliser le fait que \(A\) commute avec elle même. Pour la question 2) il fallait décomposer sa démonstration en deux temps avec le sens direct et indirect de l’équivalence.
La question 3) est une application de la notion de racine carrée de matrice, il fallait à l’aide de calculs trouver la valeur de \(A^2\) puis résoudre un système en identifiant les coefficients pour montrer que \(a=d \; \text{et} \; b=-c.\) Cela nous permet d’aboutir au fait que l’équation \(M^2=A\) admet deux solutions.
La question 4) est également une application de la notion de racine carrée de matrice, pour étudier son caractère diagonalisable il fallait montrer que la dimension associée à sa seule valeur propre 0 était 2 et non 3. La question 4) b) est un calcul de produit matriciel. La question c) nécessite d’utiliser l’indice du sujet en appliquant \(f^{p-1}\) à l’équation de liaison. Cela nous permet d’aboutir à une contradiction sur l’existence d’une matrice \(M\) qui vérifie le problème.
La question 5) demande de repérer qu’un polynôme annulateur de de \(M\) est \(X^2-1\) et que ses deux racines sont 1 et -1. Nous pouvions ensuite procéder par un raisonnement par analyse synthèse. Une analyse de dimensions de la 5) b) permet de confirmer le caractère diagonalisable de l’endomorphisme étudiée et de conclure sur le résultat de la 5) d).
La question 6) nous fait travailler ici dans le cas où \(A\) admet \(n\) racines distinctes donc est diagonalisable. Ainsi en raisonnant sur les propriétés d’une telle patrice comme le fait qu’elle soit égale à \(PDP^{-1}\) nous arrivons à montrer que la matrice \(N\) est diagonale et à établir les solutions de l’équations \(M^2=A.\)
La question 7) introduit un nouveau cas pour les valeurs propres de \(A,\) elles sont ici toutes strictement positives. \(A\) est symétrique donc diagonalisable cela nous permet de la décomposer en un produit de produit de trois matrices de la forme \(PDP^{-1}\) où \(D\) contient les racines carrés des valeurs propres sur sa diagonale. Nous avons donc bien construit la matrice attendue. Maintenant, il faut supposer l’existence de deux matrices avec les mêmes propriétés, grâce aux étapes que suggère le sujet nous pouvons montrer qu’elles sont égales d’où l’unicité.
Partie II
La première question de cette deuxième partie est une question de cours qui consiste à montrer qu’une application bilinéaire est un produit scalaire. Pour la 9) il fallait utiliser l’inégalité de Cauchy Schwarz et pour la 10) utiliser la nouvelle définition de limite d’une matrice qui vient d’être introduite.
La question 11) commence avec une simple analyse de fonction et l’utilisation d’un raisonnement par récurrence qui est demandée dans le sujet. Ensuite avec l’inégalité des accroissements finis nous pouvons montrer que Phi est \(\displaystyle \frac12\) contractante ce qui nous permettra de montrer par itération la dernière inégalité.
La question 12) a) nous fait utiliser le caractère diagonalisable de la matrice \(A\) qui découle de sa symétrie. Il faut ensuite utilise la définition par récurrence de \(M_k\) pour montrer le résultat attendu. En appliquant un raisonnement analogue à celui de la 11) nous pouvons montrer la première inégalité, la seconde utilise l’inégalité de Cauchy Schwarz utilisée précédemment. La dernière question de la partie est la première question de Python du sujet qui fait utiliser les bibliothèques rappelées en début de sujet.
Problème 2 : fonction gamma et Stirling
Ce deuxième problème nous fait étudier la fonction Gamma pour ensuite démontrer l’équivalent de Stirling.
Partie I
La première question est une question de cours qui nécessité une récurrence et une IPP. Quant à la question 2) elle consiste à réaliser une étude de fonctions et à montrer que \(h_n\) est une densité de probabilité avec du calcul. Il ne faut pas oublier de calculer la limite de \(h_n\) ou c’est \(n\) qui tend vers \(+\infty\) et non \(t.\) Pour la c), il était possible de calculer chaque membre de l’égalité pour montrer qu’ils ne sont pas égaux.
Partie II
La question 3) nous fait utiliser la linéarité de l’espérance et l’indépendance des variables pour la variance. Quant à la 4), nous travaillons autour de lois gammas, il était possible de faire une récurrence pour obtenir le résultat attendu ou d’étudier des densités.
La question 5) peut se faire en repassant aux fonctions de répartitions puis en les dérivant pour obtenir les résultats demandés. Nous pouvons appliquer le même raisonnement pour la question 6) en effectuant des calculs. Finalement c’est la définition de la convergence en loi qui nous permettra d’aboutir à la convergence vers une loi normale centrée réduite demandée dans la 7). La 8) est un calcul où il faut faire attention de ne pas appliquer l’égalité de 2) c) qui est fausse comme nous l’avons montrée.
Partie III
Cette troisième partie nous fait travailler avec des fonctions à plusieurs variables. Il fallait dans la 8) appliquer la définition de la fonction \(L\) et dans la 9) montrer le caractère \(C^1\) en utilisant la continuité de la composition et du produit. La question 10) nécessite de réaliser une étude de \(L\) et de Phi pour trouver un maximum et utiliser la définition d’un maximum ce qui nous permet d’obtenir l’inégalité attendue.
Quant à la question 11) c’est une application directe de la question 5), il faut ensuite commenter l’espérance et la variance. Il vaut ensuite étudier la variance qui tend vers 0 pour conclure sur la convergence de l’estimateur. Finalement, la question 13) consiste à construire rigoureusement un intervalle de confiance.
Les deux questions suivantes sont des question Python qui nécessitaient d’utiliser la bibliothèque scipy.special.
Partie IV
Cette quatrième et dernière partie a pour but de nous faire démontrer l’équivalent de Stirling.
Les deux premières questions sont des questions de cours où il fallait d’un côté appliquer la formule de Taylor Young puis utiliser le critère de Riemann pour confirmer la convergence de la série de terme général \(v_n.\)
La question 17) nous fait appliquer le résultat de la question 6) de la Partie II et ce résultat nous permet par calcul de montrer la 18) a). L’inégalité de la 18) b) s’obtient avec une étude de la fonction \(R.\) Finalement il fallait utiliser la convergence de \(W_n\) démontrée en fin de Partie II ainsi que le résultat de la 7) b).
La question 19) doit se faire en plusieurs étapes. Premièrement par calcul nous devons dériver \(g\) pour ensuite majorer cette expression puis utiliser le résultat de la 18) b). L’inégalité des accroissements finis accompagnée des deux résultats que nous venons de montrer permet de trouver cette nouvelle inégalité. La 19) b) doit dans un premier temps se faire en calculant chaque membre de l’égalité pour la vérifier puis nous devons passer en valeur absolue l’égalité puis intégrer.
Finalement nous arrivons à montrer l’équivalent de Stirling dont un article le concernant est disponible ici !
Retrouve toute la liste des annales ECE / Maths appliquées
Retrouve toutes nos ressources de mathématiques