L’étude de matrice particulière est un exercice récurent au concours, cela peut constituer un exercice entier pour les épreuves EDHEC/EML, ou alors une partie d’exercice pour les Parisiennes. L’objectif de cet article est de s’intéresser aux différentes propriétés des matrices de Hilbert.
Présentation de la matrice de la matrice de Hilbert
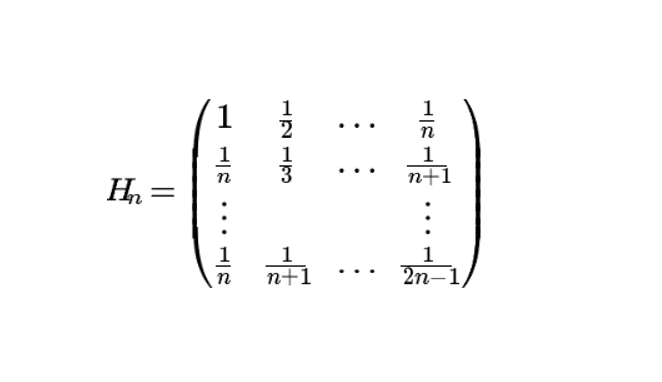
La matrice de Hilbert est la matrice \(H_n\) de terme général \(H_(i,j)=\frac{1}{i+j-1}\).
Ainsi \(H_n=\begin{pmatrix} 1 & \frac{1}{2}& \ldots
& \frac{1}{n} \\ \frac{1}{2} & \frac{1}{3}& \ldots &
\frac{1}{n+1}\\ \vdots & & & \vdots \\ \frac{1}{n}
& \frac{1}{n+1} & \ldots & \frac{1}{2n-1} \end{pmatrix}\)
Par exemple, la matrice de Hilbert de rang trois vaut : \(H_3=\begin{pmatrix} 1 & \frac{1}{2}& \frac{1}{3} \\ \frac{1}{2} & \frac{1}{3}& \frac{1}{4}\\ \frac{1}{3}
& \frac{1}{4} & \frac{1}{5} \end{pmatrix}\)
Diagonalisabilité de la matrice de Hilbert
1 – Expression de \({}^tXH_nX\)
Soit \(X=(x_0,x_1,….,x_{n-1})\) un vecteur de nombres réels.
On sait que \(\displaystyle \int_{0}^{1} t^{k+j-2} \,
\mathrm{d}t = \frac{1}{k+j-1}\)
D’où \({}^tXH_nX=\displaystyle \sum_{j=0}^{n-1}\displaystyle \sum_{i=0}^{n-1}x_i x_j \frac{1}{i+j-1}=\displaystyle \sum_{j=0}^{n-1}\displaystyle \sum_{i=0}^{n-1}x_i x_j \displaystyle \int_{0}^{1} t^{i+j-2} \,
\mathrm{d}t =\displaystyle \int_{0}^{1} (x_0+X_1t+…+x_{n-1}t^{n-1})^2\,
\mathrm{d}t \).
On note alors que pour tout vecteur \(X\), on a \({}^tXH_nX\) positif.
2 – Diagonalisabilité
\(H_n\) est une matrice symétrique, elle est donc diagonalisable. De plus, toutes ses valeurs propres sont positives.
En effet, soit \(\lambda\) une valeur propre de \(H_n\) associée au vecteur propre \(X\), \({}^tXH_nX = \lambda ||X||^2\) d’où \(\lambda\) positif.
3 – Étude du spectre
Montrons que \(0\) n’appartient pas au spectre de \(H_n\). Pour cela, on réutilise l’écriture du produit de \({}^tXH_nX\) et on montre que \({}^tXH_nX=0 \leftrightarrow X=0\).
Tout d’abord, si \(X=0\) alors on a naturellement \({}^tXH_nX=0\).
Supposons \({}^tXH_nX=0\), alors \(\displaystyle \int_{0}^{1} (x_0+X_1t+…+x_{n-1}t^{n-1})^2\,
\mathrm{d}t =0\). Or, la fonction \((x_0+X_1t+…+x_{n-1}t^{n-1})^2\) est une fonction polynomiale, donc continue sur \([0;1]\) et elle est positive, donc dire que l’intégrale vaut zéro revient à dire que la fonction est nulle. Donc, pour tout \(t\) dans \([0;1]\), \(x_0+X_1t+…+x_{n-1}t^{n-1}=0\).
C’est une fonction polynomiale de degré \(n-1\) qui admet une infinité de racines, donc c’est le polynôme nul. Ainsi, tous les coefficients sont nuls, on a donc bien \(X=0\).
Finalement, on a montré que \(0\) n’appartient pas au spectre de \(H_n\).
Inverse d’une matrice de Hilbert
Comme nous venons de le montrer, \(0\) n’est pas dans le spectre de \(H_n\), la matrice de Hilbert est donc une matrice inversible. Calculer son inverse est bien trop difficile et fastidieux, mais il existe un programme Python qui permet de calculer la matrice et son inverse.
Étude de sous-espaces propres particuliers
Soit \(\alpha\) la plus petite valeur propre de \(H_n\) et \(\beta\) la plus grande. On a \(0 \le \alpha\) car \(H_n\) n’a que des valeurs propres positives.
On montre facilement que \(\alpha ||X||^2 \le {}^tXH_nX \le \beta ||X||^2\). Cela découle du quotient de Rayleigh, cet article réexplique en détail comment montrer cette inégalité.
Soit \(V\) le sous-espace propre associé à la valeur propre \(\beta\). Montrons que \(dim(V)=1\).
Soit \(X_0= \begin{pmatrix} x_0 \\ x_1 \\ \vdots \\x_n \end{pmatrix}\) et \(|X_0|\begin{pmatrix} |x_0| \\ |x_1| \\ \vdots \\|x_n| \end{pmatrix}\) deux vecteurs de \(V\).
On montre facilement que \({}^tX_0H_nX_o \le {}^t|X_0|H_n|X_o|\). En effet \(\displaystyle \sum_{j=1}^{n}\displaystyle \sum_{i=0}^{n-1}x_i x_j \frac{1}{i+j-1} \le \displaystyle \sum_{j=1}^{n}\displaystyle \sum_{i=0}^{n-1}|x_i|| x_j| \frac{1}{i+j-1}\).
On obtient donc : \(\beta ||X||^2 \le {}^t|X_0|H_n|X_o| \le \beta ||X||^2\) d’où \({}^t|X_0|H_n|X_o| = \beta ||X||^2\). Donc \(|X_0|\) est un vecteur de \(V\).
De plus, on remarque que toutes les composantes du vecteur \(H_n|X_0|\) sont positives (produit et somme de nombre positifs !). Ainsi \(|X_0|\) n’a aucune composante nulle.
En utilisant le fait que \({}^tX_0H_nX_o = {}^t|X_0|H_n|X_o|\) (car ce sont deux vecteurs propres), on trouve que toutes les composantes de \(X_0\) sont de même signe.
Finalement, on obtient \(X_0=|X_0|\). Ainsi, on a montré que \(V\) ne contient qu’un seul et unique vecteur donc \(dim(V)=1\).
Exemple : le cas où n=2
\(H_2=\begin{pmatrix} 1 & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{3} \end{pmatrix}\)
Pour trouver les valeurs propres, on résout \(x^2- \frac{4}{3}x+\frac{1}{12}\). \(\Delta=\frac{16}{9}-\frac{1}{3}=\frac{13}{9}\). On trouve alors \(\beta=\frac{4+\sqrt{16}}{6}\) et \(\alpha=\frac{4-\sqrt{16}}{6}\). Chaque sous-espace vectoriel (le plus petit et le plus grand) est de dimension 1.
Pour aller plus loin sur la matrice de Hilbert
Tu peux résoudre le sujet HEC 2006 ECS (sujet, corrigé) pour en savoir plus sur les matrices de Hilbert. Attention, il y a des complexes dans la partie 2, mais tu peux facilement la sauter et faire directement la partie 3.
N’hésite pas à consulter toutes nos ressources mathématiques.