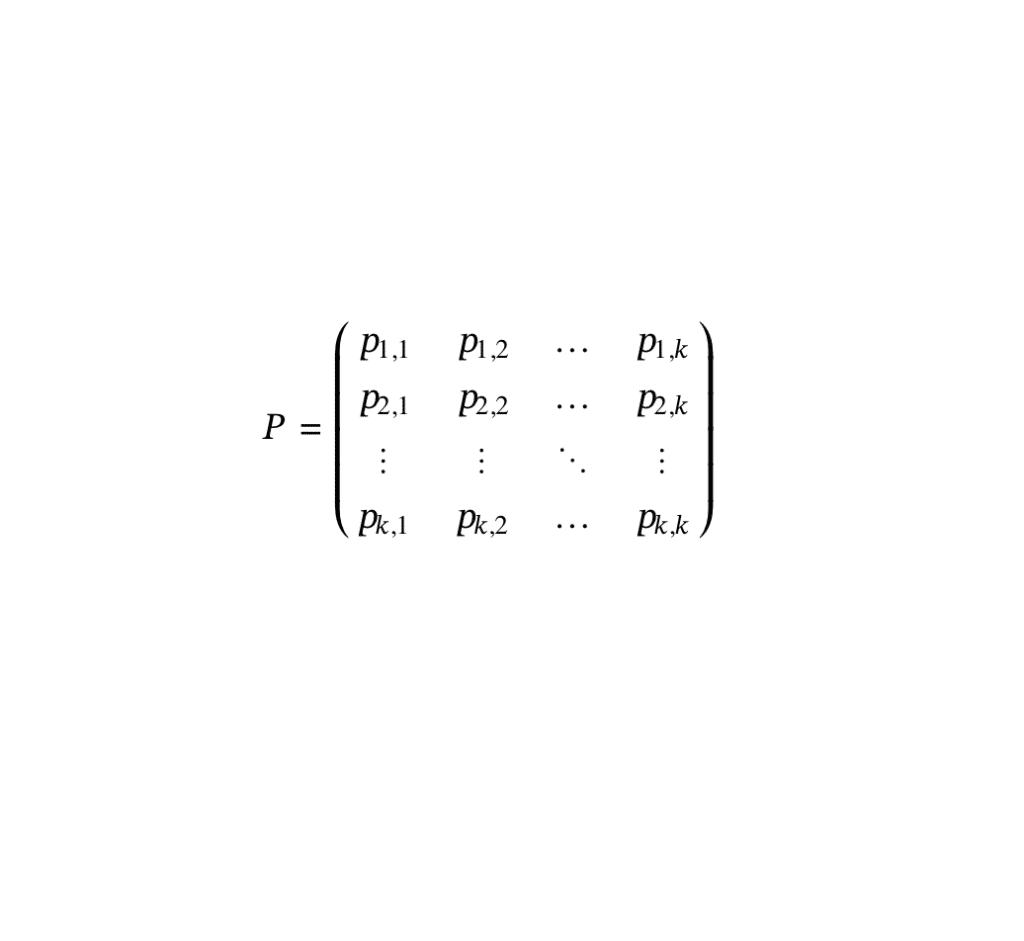On va travailler ensemble sur un thème essentiel en algèbre linéaire (hors programme) : les matrices de transition. Ces matrices se retrouvant dans de nombreux sujets de concours, il est important de maîtriser leurs caractéristiques et leurs différentes propriétés. C’est aussi l’occasion pour toi de revoir une partie fondamentale du cours de probabilités, celui des chaînes de Markov.
Rappel de cours sur les chaînes de Markov
Une chaîne de Markov est une suite de variables aléatoires \( \displaystyle (X_n)\) à valeurs dans un ensemble \( E \) fini. La chaîne de Markov exprime alors la probabilité de passer d’un état \( \displaystyle X_n\) à un nouvel état \( \displaystyle X_{n+1}\). Ainsi, on a, pour tout \(n \in \mathbb{N}\) et \( (i, j) \in E\) :
\( \displaystyle P(X_{n+1} = j \mid X_n = i, X_{n-1}, \dots) = P(X_{n+1} = j \mid X_n = i) \)
Les chaînes de Markov représentent ainsi des systèmes où l’on passe d’un état à un autre selon différentes probabilités. Ces passages sont justement décrits par une matrice de transition associée à une chaîne de Markov spécifique.
Définition d’une matrice de transition
Ainsi, à partir d’une chaîne de Markov, on peut alors définir une matrice de transition.
Soit \( E = \{1, 2, \dots, k\} \) l’ensemble des états possibles où \(k \in \mathbb{N}\). On appelle matrice de transition, la matrice carrée \( P \in M_k(\mathbb{R}) \) dont les coefficients \( p_{i,j} \) correspondent à la probabilité de transition de l’état \( i \) à l’état \( j \), et définie par :
\[
P = \begin{pmatrix}
p_{1,1} & p_{1,2} & \dots & p_{1,k} \\
p_{2,1} & p_{2,2} & \dots & p_{2,k} \\
\vdots & \vdots & \ddots & \vdots \\
p_{k,1} & p_{k,2} & \dots & p_{k,k}
\end{pmatrix}
\]
avec pour tout \( (i, j) \in E\), \( p_{i,j} = P(X_{n+1} = j \mid X_n = i) \).
Propriétés des matrices de transition
Stochasticité des matrices de transition
Une matrice de transition est stochastique. Ainsi, les coefficients \( p_{i,j} \) dans une matrice de transition représentent des probabilités de transition d’un état \(i \) vers un état \( j \). D’où :
\[ 0 \leq p_{i,j} \leq 1 \quad \text{pour tout } i, j \]
De même, comme ces coefficients définissent des probabilités, leur somme est donc égale à 1. Une autre propriété importante des matrices de transition est donc que la somme des coefficients de chaque ligne est égale à 1.
\[ \sum_{j=1}^{k} p_{i,j} = 1 \quad \text{pour tout } i \]
Note : les propriétés des matrices stochastiques s’appliquent aux matrices de transition.
Ainsi, on peut vérifier si une matrice est bien une matrice de transition à partir de ces propriétés. Par exemple, si on considère la chaîne de Markov suivante avec 3 états :
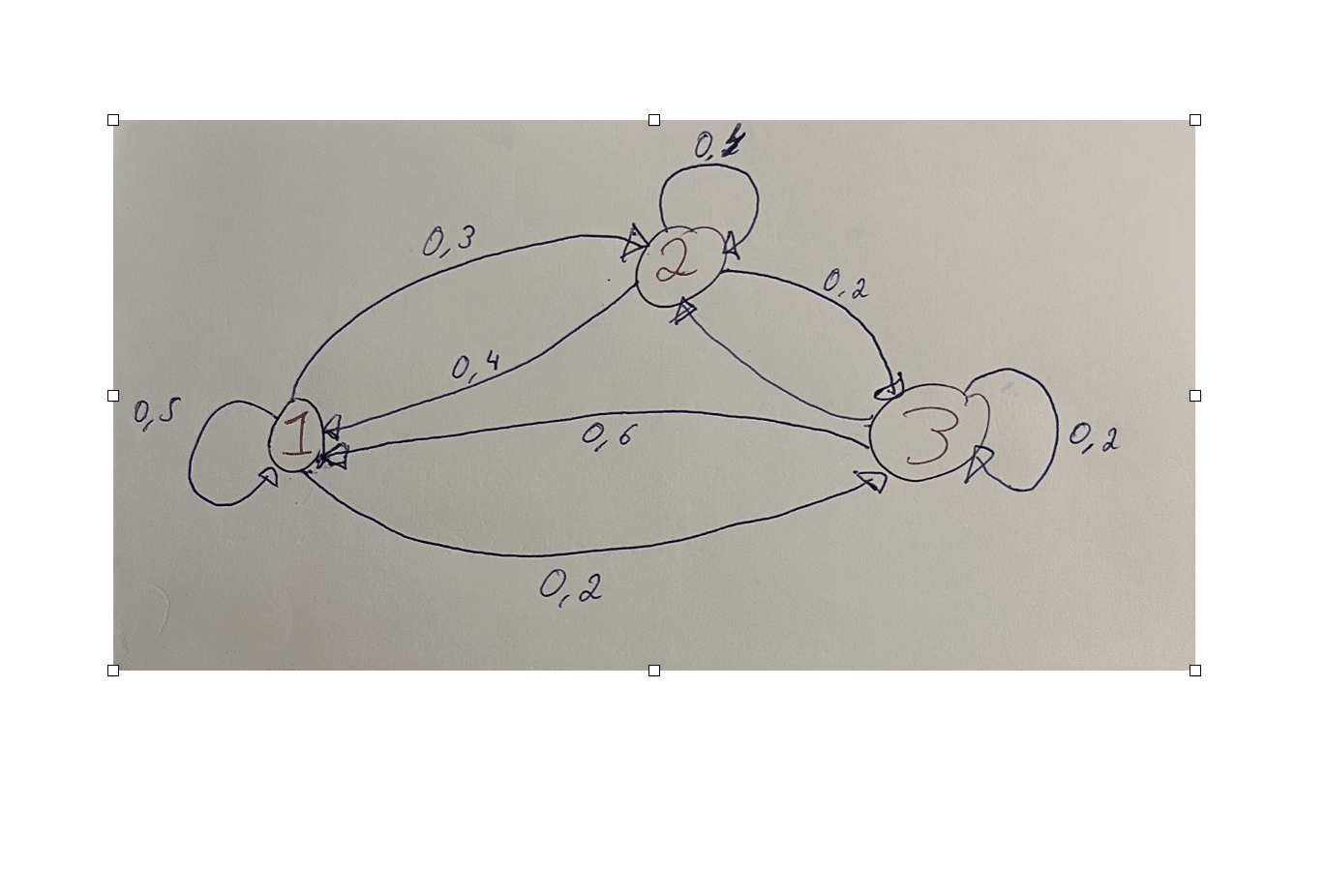
On a alors la matrice suivante à partir des probabilités :
\( P = \begin{pmatrix} 0.5 & 0.4 & 0.6 \\ 0.3 & 0.4 & 0.2 \\ 0.2 & 0.2 & 0.2\end{pmatrix} \)
Cette matrice est bien une matrice de transition, car tous les coefficients sont compris entre 0 et 1 et la somme des éléments de chaque ligne est égale à 1, puisque :
\( \begin{aligned} 0.5 + 0.3 + 0.2 &= 1 \\ 0.4 + 0.4 + 0.2 &= 1 \\ 0.6 + 0.2 + 0.2 &= 1 \end{aligned} \)
Si tu souhaites en apprendre davantage sur les matrices stochastiques hors programme, n’hésite pas à jeter un œil à cet article sur les matrices de permutation.
Puissance de matrice de transition
On choisit une matrice de transition \( P \). Alors, le passage à la puissance \( n \) de cette matrice, soit \( P^n \), renvoie les probabilités de transition entre les états \( i \) et \( j \) après plusieurs transitions successives.
Par exemple, si on reprend la matrice \( P \) et qu’on cherche les probabilités de transition après \( 5 \) étapes. Il nous suffit de calculer la puissance à \( P^5 \) et les éléments obtenus représenteront les probabilités recherchées.
\( P^5 = \begin{pmatrix} 0.48889 & 0.31111 & 0.2 \\ 0.48888 & 0.31112 & 0.2 \\ 0.4889 & 0.3111 & 0.2 \end{pmatrix} \)
État stationnaire
Une chaîne de Markov admet un état stationnaire si et seulement si le vecteur de probabilités \(\pi = (\pi_1, \pi_2, \dots, \pi_k)\) vérifie la relation suivante :
\[ \pi P = \pi \]
Autrement dit, le vecteur \( \pi \) des probabilités reste inchangé après l’application de la matrice de transition \( P \). Ainsi, pour chaque \( i \in E \), la probabilité \( \pi_i \) de se trouver dans l’état \( i \) à l’instant \( n+1 \) est égale à la probabilité de se trouver dans l’état \( i \) à l’instant \( n \).
De plus, on traduit souvent l’état stationnaire par un système d’équations linéaires qui inclut donc la matrice de transition \( P \) :
\[ \begin{pmatrix} \pi_1 & \pi_2 & \dots & \pi_k \end{pmatrix} \begin{pmatrix} p_{1,1} & p_{1,2} & \dots & p_{1,k} \\ p_{2,1} & p_{2,2} & \dots & p_{2,k} \\ \vdots & \vdots & \ddots & \vdots \\ p_{k,1} & p_{k,2} & \dots & p_{k,k} \end{pmatrix} = \begin{pmatrix} \pi_1 \\ \pi_2 \\ \vdots \\ \pi_k \end{pmatrix} \]
On peut aussi l’écrire sous la forme :
\[ \pi_1 = \pi_1 p_{1,1} + \pi_2 p_{2,1} + \dots + \pi_k p_{k,1} \] \[ \pi_2 = \pi_1 p_{1,2} + \pi_2 p_{2,2} + \dots + \pi_k p_{k,2} \] \[ \vdots \] \[ \pi_k = \pi_1 p_{1,k} + \pi_2 p_{2,k} + \dots + \pi_k p_{k,k} \]
Le concept d’état stationnaire est particulièrement utile afin de prédire le comportement d’un système de Markov et de déterminer si une chaîne de Markov atteint une forme de stabilité à partir d’un certain rang \( n \)
Exprimer une matrice de transition en langage Python
Les sujets de concours faisant de plus en plus intervenir des exercices avec du Python, il peut être utile de maîtriser les matrices de transition dans ce langage. Ici, on va s’intéresser particulièrement à la puissance de matrice de transition qui permet de connaître la probabilité de passer d’un état à un autre après plusieurs transitions successives dans un système de Markov.
On reprend alors la matrice de notre exemple et on cherche cette-fois à calculer la matrice de transition après deux étapes. On a donc le code suivant :
Ainsi, si tu cherches, la probabilité de passer de l’état 1 à l’état 3 après deux étapes, il te suffit de regarder l’élément \( (1, 3) \) de la matrice \( P^2 \), donnée par ce code Python.
Remarque : inutile de connaître ce code Python par cœur, mais tu peux essayer de le comprendre au cas où il te serait demandé de compléter des codes similaires dans un sujet de concours. Tu peux par ailleurs retrouver ici tous nos autres articles consacrés au langage Python.
Annales où tu pourras retrouver des matrices de transition
Le thème des matrices de transition est d’autant plus intéressant et utile à travailler qu’il est tombé plusieurs fois lors des derniers concours de maths appliquées. Je te mets les liens de deux récents sujets où tu pourras retrouver cette formule :
- Maths II ESSEC 2023 Partie II (je te recommande particulièrement d’effectuer ce sujet, car de nombreuses questions sont accessibles)
- Maths EDHEC 2024 Problème
Et tu peux retrouver ici les corrigés de ces sujets :
Conclusion
Tu connais maintenant tout sur la matrice de transition ! Tu es désormais capable de donner sa définition et son lien avec les chaînes de Markov et ses différentes propriétés (état stationnaire, stochasticité des lignes, changement de bases…). Tu es même capable d’exprimer la puissance d’une matrice de transition en langage Python !
J’espère que cet article t’a plu. Tu peux retrouver ici toutes nos autres ressources mathématiques et continuer à t’exercer sur d’autres annales grâce à notre méga-répertoire.