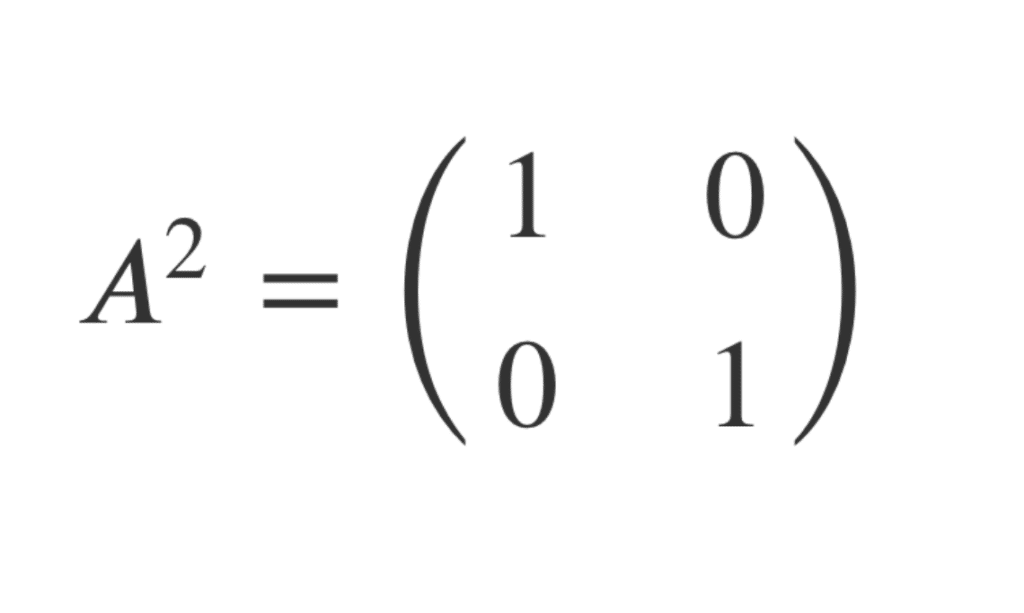Aujourd’hui, je voulais aborder avec toi une notion que l’on retrouve souvent dans les annales, et en particulier dans les exercices d’oraux : les matrices 2-symétriques !
Nous allons voir ensemble de quoi il s’agit et aborder les principales propriétés que l’on va démontrer pour que tu sois prêt·e à les affronter dès ta prochaine khôlle.
Présentation des matrices 2-symétriques
Prenons un exemple pour que ce soit plus visuel. On pose la matrice \(A=\begin{pmatrix} 1 & 1 \\ 0& -1\end{pmatrix}\). Tu n’as a priori rien à dire sur \(A\), qui n’est pas symétrique.
On calcule \(A^2\). On a alors : \(A^2=\begin{pmatrix} 1 & 0 \\ 0
& 1\end{pmatrix}\). \(A^2\) est donc symétrique (c’est même la matrice identité). On dira alors que A est 2-symétrique.
Définition
Voyons une définition plus générale.
Soit \(n \ge 2\). On dit que \(A \in \mathcal{M}_{n}(\mathbb{R})\) est « 2-symétrique » si \(A^2\) est symétrique.
Propriétés des matrices 2-symétriques
- Les matrices 2-symétriques de taille 2 sont toutes de la forme \(\begin{pmatrix} a & b \\ c & -a\end{pmatrix}\) ou \(\begin{pmatrix} a & b \\ b & d\end{pmatrix}\)
Pour montrer cela, on se reporte à la définition d’une matrice symétrique \(A={}^tA\), mais on l’applique cette fois à \(A^2\). En posant \(A=\begin{pmatrix} a & b \\ c & d\end{pmatrix}\), on obtient le résultat escompté.
- Toute matrice symétrique est 2-symétrique
En effet, si \(A={}^tA\), alors \({}^t(A^2)=({}^tA)^2=A^2\)
- Si \(A\) est inversible et 2-symétrique, alors \(A^{-1}\) est 2-symétrique
On applique les règles de transposition : \(({}^tA^{-1})^2=({}^tA^2)^{-1}=(A^2)^{-1}=(A^{-1})^2\)
- Si \(A\) est antisymétrique, alors \(A\) est 2-symétrique
De la même façon, on a \({}^t(A^2)=({}^tA)^2=(-A)^2=A^2\)
- Soient \(A\) et \(B\) deux matrices 2-symétriques. On suppose que \(A\) et \(B\) commutent. Alors \(AB\) est 2-symétrique
En faisant bien attention aux règles de multiplication des matrices (tout marche bien ici, car \(A\) et \(B\) commutent), \({}^t(AB)^2={}^t(ABAB)={}^t(A^2B^2)={}^t(A^2){}^t(B^2)=B^2A^2=(AB)^2\)
Et voilà le principal à savoir 🙂 Pour continuer à t’entraîner, tu peux te demander sous quelle condition \(A+B\) est 2-symétrique, ou encore faire le lien avec les endomorphismes.
Tu peux retrouver un exemple de matrice 2-symétrique dans l’annale d’oral 1.2 ESCP 2021
N’hésite pas à consulter toutes nos autres ressources en mathématiques ici.