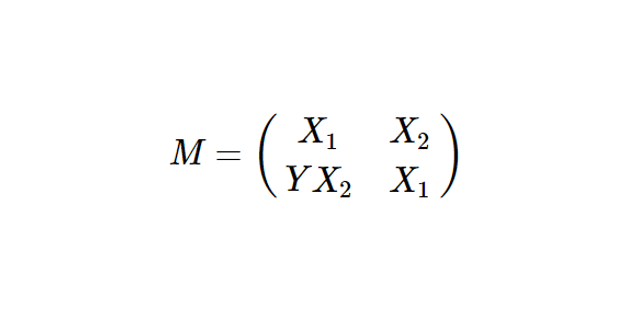Les matrices aléatoires impressionnent à première vue, car elles traitent de probabilité et d’algèbre, mais avec de la rigueur, tu pourras maîtriser ce thème. Elles tombent souvent à l’oral, mais elles sont déjà tombées à l’écrit. Voici donc un article pour t’aider.
Définition d’une matrice aléatoire
Une matrice aléatoire est une matrice composée de coefficients aléatoires, c’est-à-dire que ses coefficients sont des variables aléatoires.
Une telle matrice est donc engendrée par des vecteurs aléatoires.
Exemple
Soient \( p \in [0,1] \), \( n \in \mathbb{N}^* \), \( \lambda \in \mathbb{R}^* \), \( X \sim \mathcal{B}(p) \), \( Y \sim \mathcal{B}(n,p) \), \( Z \sim \mathcal{P}(\lambda) \).
Voici une matrice aléatoire \(M\) engendrée à partir de ces variables aléatoires :
\[ M = \begin{pmatrix} 2X & Y \\ 0
& 4Z\end{pmatrix} \]
Donc, en fonction des valeurs que prennent les variables, on peut avoir :
\[
M = \begin{pmatrix}
0 & n-1 \\
0 & 32
\end{pmatrix}
\text{ ou }
M = \begin{pmatrix}
2 & 0 \\
0 & 0
\end{pmatrix}
\]
On peut définir des matrices aléatoires de toutes les tailles (\(4×4, 10×3\), etc). Mais les matrices auxquelles tu auras affaire seront généralement des matrices 2×2 par souci de simplicité.
Quelles méthodes faut-il connaître ?
Les exercices qui traitent de matrices aléatoires ne représentent pas un changement drastique. Pour réussir ces questions, il faut connaître son cours d’algèbre par cœur, notamment sur les conditions d’inversibilité, de diagonalisation, mais il faut aussi beaucoup rigueur dans le dénombrement.
Cependant, il n’y a rien qui soit drastiquement différent dans les méthodes à appliquer. Les questions restent quasiment les mêmes que dans les exercices classiques d’algèbre. Au lieu d’avoir « Sous quelles conditions M est inversible/diagonalisable », les questions sont plutôt « Quelle est la probabilité que M soit inversible, diagonalisable ? ».
Exercice classique d’oral sur les matrices aléatoires
Si tu tombes sur des matrices aléatoires à l’oral, tu n’es pas obligé(e) de tout réussir parfaitement, les jurys et correcteurs testent principalement ta connaissance de ton cours d’algèbre, avec ta capacité d’adaptabilité en mixant algèbre et probabilités.
Comme tu vas le voir avec cet exercice, les méthodes appliquées ne sont pas nouvelles, mais il faut être très rigoureux pour ne pas faire d’erreurs de calcul. Donc, ce n’est pas grave si tu ne réussis pas tout parfaitement, mais il faut savoir montrer que tu connais ton cours !
Énoncé de la QSP n° 2 HEC 2023
Soient \( X_1 \) et \( X_2 \) des variables aléatoires indépendantes de même loi.
Soit \( Y \) une variable aléatoire indépendante des deux autres telle que \( Y(\Omega) = \{-1, 1\} \) et \( P(Y = 1) = p \in ]0, 1[ \).
On pose :
\[
M = \begin{pmatrix}
X_1 & X_2 \\
Y X_2 & X_1
\end{pmatrix}
\]
- On suppose pour cette question que \( X_1 + 1 \) suit une loi géométrique de raison \( \frac{1}{3} \). Quelle est la probabilité que \( M \) soit inversible ?
- On suppose pour cette question que \( X_1 \) suit une loi de Poisson de paramètre \( \lambda \).
Quelle est la probabilité que \( M \) soit diagonalisable ?
Correction
1. On cherche la probabilité que la matrice ne soit pas inversible.
On sait que : \( M \) est inversible si et seulement si \( \det(M) \neq 0 \). Cependant, il est trop coûteux de calculer toutes les possibilités où \( \det(M) \neq 0 \). Nous allons donc travailler avec la probabilité que \( M \) soit non inversible.
On a :
\[
\begin{aligned}
\mathbb{P}(M \text{non inversible}) &= \mathbb{P}(\det(M) = 0) \\
&= \mathbb{P}(X_1^2 – Y X_2^2 = 0) \\
&= \mathbb{P}(X_1^2 = Y X_2^2) \\
&= \mathbb{P}[(X_1 = X_2) \cap (Y = 1)] + \mathbb{P}[(X_1 = X_2 = 0) \cap (Y = -1)] \\
&\quad \text{avec le système complet d’événements associé à } Y \\
&= \mathbb{P}(X_1 = X_2)\mathbb{P}(Y = 1) + \mathbb{P}(X_1=0)\mathbb{P}(X_2 = 0)\mathbb{P}(Y = -1) \\&\quad \text{par indépendance des évènements} \\
&= p \sum_{k=0}^{+\infty} \mathbb{P}([X_1 = k] \cap [X_2 = k]) + (1 – p) \cdot \frac{1}{3}\cdot \frac{1}{3} \\
&= p \sum_{k=0}^{+\infty} \mathbb{P}([X_1 +1 = k +1)\mathbb{P}(X_2 +1= k+1)+ (1 – p) \cdot \frac{1}{9} \quad \text{par indépendance de} X_1 \text{et} X_2\end{aligned}
\]
On fait \(X_1 +1 = k + 1\) car on connaît la loi de \(X_1 + 1\).
On a donc :
\[
\begin{aligned}
\mathbb{P}(M \text{ non inversible}) &= p \sum_{k=0}^{+\infty} (\frac{2}{3})^{k}\frac{1}{3} \cdot (\frac{2}{3})^{k}\frac{1}{3} + (1 – p) \cdot \frac{1}{9} \\
&= \frac{1}{9} \left( p \sum_{k=0}^{+\infty} \left( \frac{2}{3} \right)^{2k} + (1 – p) \right)
\end{aligned}
\]
En passant au complémentaire, on a :
\[
\fbox{\(\mathbb{P}(M \text{ est inversible}) = 1 – \left( p \cdot \frac{1}{5} + (1 – p) \cdot \frac{1}{9} \right)\)}
\]
2. Sachant que c’est un exercice sans préparation, si tu réussis à avancer sur la première question, cela sera déjà très bien. Je laisse la possibilité aux plus vaillants d’aller voir la correction de la deuxième question.
Les matrices aléatoires en Python
Pour rappel, voici la matrice \(M\) introduite dans l’exemple au début de l’exercice :
\[ M = \begin{pmatrix} 2X & Y \\ 0
& 4Z\end{pmatrix} \]
Voici comment générer cette matrice en Python :
Annales traitant des matrices aléatoires
La plupart des annales sont des annales d’oraux, tant à l’HEC qu’à l’ESCP. Chaque année, des étudiants tombent dessus et tu pourras retrouver sur ces PDF des exercices à ce propos.
À l’écrit, tu peux regarder le premier exercice du maths EDHEC 2008, c’est un exercice principalement d’algèbre, mais qui fait le lien avec les probabilités à la dernière question. Le lien avec les probabilités est dans la continuité de l’exercice et si tu ne te laisses pas impressionner par les variables aléatoires dans une matrice, tu pourras résoudre la dernière question sans souci. Voici la correction aussi.
En faisant quelques exercices, tu seras fin prêt(e) pour maîtriser les matrices aléatoires.
N’hésite pas à consulter toutes nos autres ressources mathématiques.