Major Prépa > Académique > Mathématiques > Les matrices centrosymétriques (hors programme ECG)
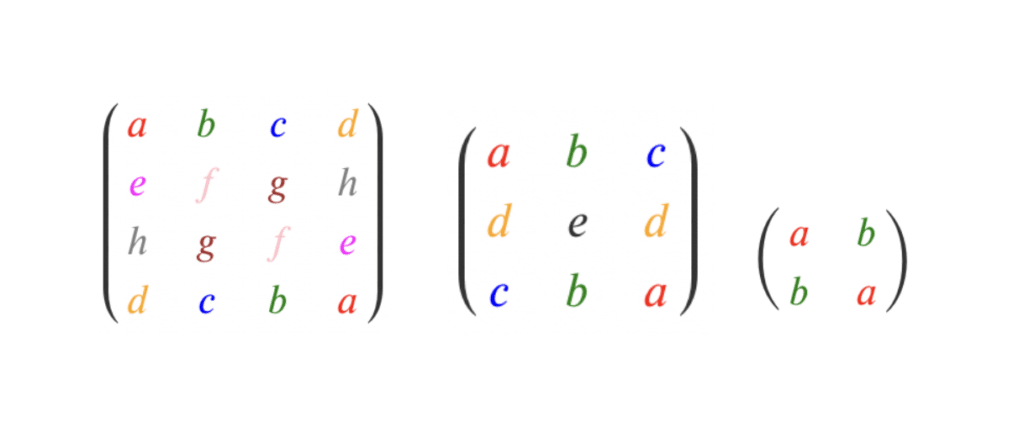
Les notions hors programme se destinent surtout aux candidats qui visent les trois Parisiennes. Cet article te propose de décortiquer la notion de matrice centrosymétrique, assez récurrente dans les sujets de concours, pour mieux t’aider à comprendre avec des exemples et des schémas. Tu retrouveras également une liste des propriétés intéressantes de cette notion afin d’être sensibilisé(e) et ne pas être pris(e) au dépourvu le jour J (cela te simplifiera aussi la tâche pour ficher).
La notion de matrice centrosymétrique expliquée en français
Une matrice centrosymétrique est une matrice carrée qui est symétrique autour de son centre. Autrement dit, le point central de la matrice est un centre de symétrie. C’est aussi simple que cela !
Exemples de matrices centrosymétriques de différents ordres
- Pour une matrice \(2×2\), une matrice centrosymétrique est de la forme \( \begin{pmatrix}
\color{red}{a} & \color{green}{b} \\
\color{green}{b} & \color{red}{a}
\end{pmatrix} \)
\( \begin{pmatrix}
\color{red}{2} & \color{green}{3} \\
\color{green}{3} & \color{red}{2}
\end{pmatrix} \) est donc une matrice centrosymétrique d’ordre 2. - Pour une matrice \(3×3\), une matrice centrosymétrique est de la forme \( \begin{pmatrix} \color{red}{a} & \color{green}{b} & \color{blue}{c}
\\ \color{orange}{d} & e & \color{orange}{d} \\ \color{blue}{c} & \color{green}{b} & \color{red}{a}
\end{pmatrix} \)
\( \begin{pmatrix} \color{red}{4} & \color{green}{7} & \color{blue}{2}
\\ \color{orange}{5} & 8 & \color{orange}{5} \\ \color{blue}{2} & \color{green}{7} & \color{red}{4}
\end{pmatrix} \) est donc une matrice centrosymétrique d’ordre 3. - Pour une matrice \(4×4\), une matrice centrosymétrique est de la forme \( \begin{pmatrix}\color{red}{a} & \color{green}{b} & \color{blue}{c} & \color{orange}{d}\\\color{magenta}{e} & \color{pink}{f} & \color{brown}{g}& \color{grey}{h} \\\color{grey}{h} & \color{brown}{g} & \color{pink}{f} & \color{magenta}{e}\\\color{orange}{d} &\color{blue}{c}&\color{green}{b}&\color{red}{a}\end{pmatrix} \)
\( \begin{pmatrix}\color{red}{1} & \color{green}{7} & \color{blue}{3} & \color{orange}{6}\\\color{magenta}{12} & \color{pink}{7} & \color{brown}{1}& \color{grey}{4} \\\color{grey}{4} & \color{brown}{1} & \color{pink}{7} & \color{magenta}{12}\\\color{orange}{6} &\color{blue}{3}&\color{green}{7}&\color{red}{1}\end{pmatrix} \) est une matrice centrosymétrique d’ordre 4.
Définition mathématique d’une matrice centrosymétrique
Soit \(M \in \mathcal{M}_{n}(\mathbb{K})\) l’ensemble des matrices carrées d’ordre \(n\).
On note \( a_{i,j}\) le coefficient de la \(i^{ème}\) ligne et \(j^{ème}\) colonne.
\(M\) est dite centrosymétrique si et seulement si \( \forall (i,j) \in ([\![1,n]\!])^2\), on a : \( a_{i,j}=a_{n-i+1,n-j+1}\)
On peut aussi donner une caractérisation d’une matrice centrosymétrique
Soit \(J\) la matrice ayant des \(1\) sur son antidiagonale et des \(0\) ailleurs de cette forme :
\( J=\begin{pmatrix}
0 & \cdots & 0 & 1 \\
\vdots & ⋰ & ⋰ & 0 \\
0& ⋰ & ⋰ & \vdots \\
1 & 0 & \ldots & 0
\end{pmatrix} \)
Une matrice \(M\) du même ordre que \(J\) est centrosymétrique si et seulement si \( MJ = JM \)
Quelques propriétés sur les matrices centrosymétriques
On note désormais \(\mathcal{C}\) l’ensemble des matrices centrosymétriques.
- \(\forall n \in [\![2,+\infty]\!], I_n \in \mathcal{C}\). La matrice identité est donc toujours centrosymétrique.
- L’ensemble \( \mathcal{C}\) des matrices centrosymétriques d’ordre \(n\) est un sous-espace vectoriel de \(\mathcal{M}_{n}(\mathbb{K})\) (si n est pair, ce sous-espace vectoriel est de dimension \(\frac{n^2}{2}\), et si n est impair, il est de dimension \(\frac{(n+1)^2}{2}\)).
- Si \(A \in \mathcal{C} \), alors \( {}^tA \in \mathcal{C} \), ce qui signifie que si une matrice \(A\) est centrosymétrique, alors sa transposée est aussi centrosymétrique.
- Le produit matriciel de deux matrices centrosymétriques est encore une matrice centrosymétrique.
Démonstration : Soient \(A\) et \(B\) deux matrices centrosymétriques de \( \mathcal{M}_{n}(\mathbb{K})\), et \(Y=AB\).
\(
\begin{align}
\forall (i,j) \in ([\![1,n]\!])^2, y_{i,j} &=\displaystyle \sum_{k=1}^{n} a_{i,k}b_{k,j} \text{ (définition du produit matriciel)}\\
&=\displaystyle \sum_{k=1}^{n} a_{n-i+1,n-k+1}b_{n-k+1,n-j+1} \text{ (car } A \text{ et } B \text{ sont centrosymétriques}) \\
&=\displaystyle \sum_{s=1}^{n} a_{n-i+1,s}b_{s,n-j+1}\text{ (changement d’indice : } s=n-k+1)\\
&=y_{n-i+1,n-j+1} \text{ (à nouveau la définition du produit matriciel) }
\end{align}
\)
Au total, \(\forall (i,j) \in ([\![1,n]\!])^2, y_{i,j} = y_{n-i+1,n-j+1} \) donc \(Y\) est bien centrosymétrique, ce qui prouve que le produit de deux matrices centrosymétriques est une matrice centrosymétrique.
- Soit \(A \in \mathcal{C}\), alors \(A^{-1} \in \mathcal{C}\). Autrement dit, l’inverse d’une matrice centrosymétrique (à condition qu’elle soit inversible) est aussi une matrice centrosymétrique.
Démonstration : Soit \(A\) une matrice inversible centrosymétrique et \(\mathcal{C}\) l’ensemble des matrices centrosymétriques.
Considérons l’endomorphisme \( f : \begin{cases} \mathcal{C} \to \mathcal{C} \\
X \mapsto AX \end{cases} \)
(Justifié, car \(X \in \mathcal{C}\) et \(A \in \mathcal{C}\) donc d’après le point précédent, \(AX \in \mathcal{C}\))
On peut remarquer que \( \text{Ker}(f)={0}\) car \(A\) est inversible (donc \(0\) n’est pas valeur propre de \(A\) et ainsi, il n’existe pas de vecteurs propres associés à \(0\) qui pourraient constituer les colonnes d’une matrice multipliant A pour donner une matrice nulle).
Or, on a vu que \(\mathcal{C}\) est un espace de dimension finie, et donc comme f est un endomorphisme dans un espace de dimension finie, on a injectivité \(\Leftrightarrow\) surjectivité \(\Leftrightarrow\) bijectivité.
Ainsi, comme on a prouvé la bijectivité, \( \exists!M \in \mathcal{C}\) telle que \(AM=I_{n}\) puisque \(I_{n} \in \mathcal{C}\).
Enfin, \(M=A^{-1}\) donc \(A^{-1}\) est centrosymétrique aussi.
Bonus : un programme Python sur la notion de matrice centrosymétrique
Voici un petit programme Python qui prend en argument une matrice \(M\) et qui renvoie True si elle est centrosymétrique et False sinon.

Les sujets de concours avec la notion de matrice centrosymétrique
N’hésite pas à consulter toutes nos ressources mathématiques.



