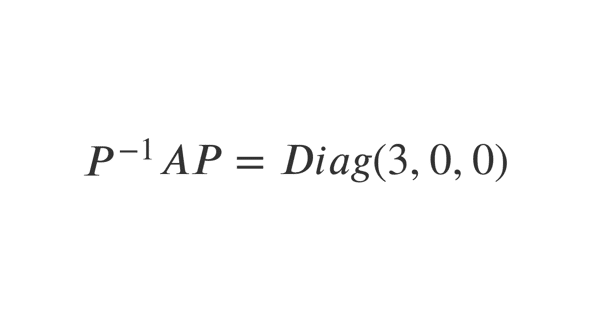Salut à toi ! On se retrouve aujourd’hui pour démontrer un résultat hors programme qui se cache dans bien des sujets d’écrits et d’oraux : les matrices codiagonalisables. C’est donc l’occasion pour toi d’en apprendre un peu plus sur le programme, tout en ayant un coup d’avance lorsque tu tomberas sur des sujets semblables. C’est parti !
La notion de codiagonalisabilité expliquée en français
Plusieurs matrices sont dites codiagonalisables ou simultanément diagonalisables si elles sont semblables à des matrices diagonales dans une même base.
Un exemple concret de deux matrices codiagonalisables
On considère \(A\) et \(B\) les deux matrices de \( \mathcal{M}_{3}
(\mathbb{R}) \) suivantes :
\[ A = \begin{pmatrix} 1 & 1 & -1
\\ 1 & 1 & -1 \\ -1 & -1 & 1
\end{pmatrix} \]
\[ B=\begin{pmatrix} 2 & 1 & -1
\\ -2 & 5 & -1 \\ -4 & 2 & 2
\end{pmatrix} \]
On a clairement \( Sp(A) =\) {\(0,3\)} et \(A\) diagonalisable puisque symétrique réelle (le fameux théorème spectral). Le sous-espace propre \( \text{Ker}(A-3I_3) \) est dirigé par le vecteur \( (1,1,-1) \). Le sous-espace propre \( \text{Ker}(A) \) est dirigé par les vecteurs \( (1,1,2) \) et \( (0,1,1) \).
D’autre part \( Sp(B) =\) {\(1,4\)}. On remarque que le sous-espace propre \( \text{Ker}(B-4I_3) \) est dirigé par les vecteurs \( (1,1,-1) \) et \( (0,1,1) \). D’autre part, le sous-espace propre \( \text{Ker}(B-I_3) \) est dirigé par le vecteur \( (1,1,2) \).
En notant \[ P = \begin{pmatrix} 1 & 1 & 0
\\ 1 & 1 & 1 \\ -1 & 2 & 1
\end{pmatrix} \]
Nous avons : \( P^{-1}AP= Diag(3,0,0) \) et \( P^{-1}BP= Diag(4,1,4) \)
\( A\) et \(B\) sont codiagonalisables puisqu’elles sont diagonalisables dans la même base \( \mathcal{B}= ((1,1,-1), (1,1,2), (0,1,1)) \).
Énoncé du théorème hors programme
Soient \(A\),\(B \in\mathcal{M}_{n}(\mathbb{K}) \) deux matrices diagonalisables.
\(A\) et \(B\) sont codiagonalisables si, et seulement si, \(A\) et \(B\) commutent.
Nous pouvons même généraliser, mais cela nous est moins utile…
Soient \(A_1\), \(… \),\(A_p \in\mathcal{M}_{n}(\mathbb{K}) \) p matrices diagonalisables.
\(A_1\),…,\(A_p\) sont codiagonalisables si, et seulement si \(A_1\), \(…\) ,\(A_p\) commutent deux à deux.
Démonstration du théorème hors programme
Soit \(E\) un espace vectoriel de dimension finie \(n \in \mathbb{N}\). Soient \(A\),\(B \in\mathcal{M}_{n}(\mathbb{K}) \) deux matrices diagonalisables.
\( \fbox{\(\Rightarrow\)}\) On suppose que \(A\) et \(B\) sont codiagonalisables
On suppose donc : \( \exists P \in GL_n(\mathbb{K}), \exists D_1,D_2 \) diagonales tels que \( P^{-1}AP=D_1 \) et \(P^{-1}BP=D_2\).
Il vient alors : \(AB=(PD_1)(P^{-1}P)(D_2P^{-1})=P(D_1D_2)P^{-1}=P(D_2D_1)P^{-1}=BA \)
Les matrices \(A\) et \(B\) commutent bien.
\( \fbox{\(\Leftarrow\)}\) On suppose que \(A\) et \(B\) commutent
Notons \(u\) et \(v\) les endomorphismes canoniquement associés à \(A\) et à \(B\).
Intéressons-nous de plus près à \(u\) : \(u\) est diagonalisable puisque \(A\) est diagonalisable. Notons \( \lambda_1,…,\lambda_p, p \in [\![1,n]\!] \) les valeurs propres de notre endomorphisme \(u\).
- En adoptant la notation suivante : \( \text{Ker}(u-\lambda_iId)=E_{\lambda_i}(u) \), la CNS de diagonalisabilité nous permet d’écrire que \( E= \displaystyle \bigoplus_{i=1}
^{n} E_{\lambda_i}(u) \). - Soit \( i \in [\![1,p]\!] \). \( \forall x \in E_{\lambda_i}(u), (u\circ v)(x)=(v \circ u)(x)=\lambda_i v(x) \). Donc \( E_{\lambda_i}(u)\) est stable par \(v\).
- Comme \(v\) est un endomorphisme diagonalisable, \( \displaystyle v_{|E_{\lambda_i}(u)}^{|E_{\lambda_i}(u)}\) l’est aussi. En notant \( \mathcal{B}_i\) une base de vecteurs propres de cet endomorphisme et en considérant la base \( \mathcal{B}= \displaystyle\bigcup_{k=1}^{n} \mathcal{B}_{k}\) adaptée à la supplémentarité \( E= \displaystyle \bigoplus_{i=1}^{n} E_{\lambda_i}(u)\).
Les représentations matricielles de \(u\) et \(v\) dans \(\mathcal{B}\) sont bien diagonales, on peut conclure : \(A\) et \(B\) sont deux matrices codiagonalisables.
Voilà ! Cet article de Major-prépa portant sur la notion de codiagonalisabilité touche à sa fin, j’espère qu’il t’aura été utile. Tu trouveras d’autres articles de maths ici !