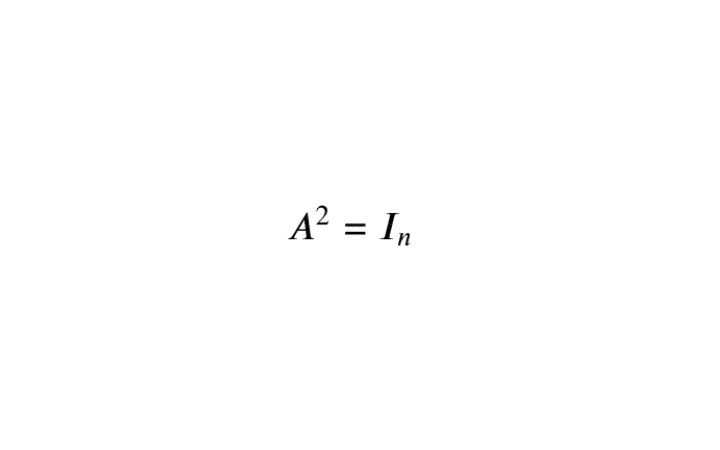On se retrouve pour étudier une nouvelle notion hors programme : les matrices involutives. C’est donc l’occasion pour toi d’approfondir ta maîtrise de l’algèbre, tout en ayant un coup d’avance si cette notion (re)tombe aux concours.
Définition d’une matrice involutive
Une matrice involutive est une matrice carrée qui, lorsqu’elle est multipliée par elle-même, donne la matrice identité.
Ainsi, \(A \in \mathcal{M}_{n}(\mathbb{R})\) est dite involutive si :
\[\fbox{\(A^2 = I_n\)}\]
Or, par propriété de l’inversibilité, on sait que \(AB = I_n \Leftrightarrow BA = I_n \Leftrightarrow B = A^{-1},\)
d’où \(A\) est inversible et égale à son propre inverse.
On peut donc étoffer notre définition d’une matrice involutive :
\[\fbox{Une matrice involutive est une matrice carrée égale à sa propre matrice inverse, telle que \(A = A^{-1}\) et \(A^2 = I_n\)}\]
Premiers exemples simples
Pour bien appréhender cette notion de matrice involutive, intéressons-nous dans un premier temps à des exemples simples :
- Soit \(A = \begin{pmatrix} 4 & -1 \\ 15 & -4\end{pmatrix}.\) Par calcul matriciel, on obtient que \(A^2 = \begin{pmatrix} 4 & -1 \\ 15 & -4\end{pmatrix}\begin{pmatrix} 4 & -1 \\ 15 & -4\end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix} = I_2,\)
d’où \(A\) est bien involutive et \(A = A^{-1}.\) - Soit \(B = \begin{pmatrix} 2 & 1 & 1\\ -1 & 0 & -1 \\ -2 & -2 & -1\end{pmatrix}.\) Toujours par calcul matriciel, on obtient que \(B^2 = \begin{pmatrix} 2 & 1 & 1\\ -1 & 0 & -1 \\ -2 & -2 & -1\end{pmatrix}\begin{pmatrix} 2 & 1 & 1\\ -1 & 0 & -1 \\ -2 & -2 & -1\end{pmatrix} = I_3,\) d’où \(B\) est également une matrice involutive.
D’où vient la notion de matrice involutive ?
Pour bien assimiler cette notion, il faut faire le lien avec la notion d’involution. Une involution est en fait une application bijective qui est sa propre réciproque.
Ainsi, pour un ensemble \(E\) non vide, on dit que \(f : E \to E\) est involutive si \(\forall x \in E, f( f(x)) = x.\)
Peut-être que ce résultat te dit quelque chose car, en algèbre linéaire, les endomorphismes involutifs sont appelés des symétries. Je t’invite ainsi à consulter cet article qui s’attarde sur la notion de symétrie, grandement reliée à celle de matrice involutive.
Principales propriétés des matrices involutives
Désormais, intéressons-nous aux principales propriétés concernant les matrices involutives. Si ces propriétés ne sont pas nécessairement à connaître par cœur, elles restent intéressantes et te permettent d’approfondir ton aisance avec l’algèbre.
\[\fbox{Le produit de deux matrices involutives qui commutent est une matrice involutive.}\]
\[\fbox{Le spectre d’une matrice involutive est compris dans {1; -1}}\]
\[\fbox{\(A \in \mathcal{M}_{n}(\mathbb{R})\) est une matrice involutive et symétrique \(\Rightarrow A\) est une matrice orthogonale}\]
\[\fbox{Si \(A\) est une matrice involutive, alors \(\forall n \in\mathbb{N}, A^n\) est une matrice involutive.}\]
\[\fbox{Si \(A\) est une matrice involutive, alors \(\forall n \in\mathbb{N}, A^n = I_n\) si \(n\) est pair, autrement \(A^n = A\) si \(n\) est impair.}\]
Démonstrations intéressantes de ces propriétés
Si les propriétés au-dessus sont intéressantes, le plus utile est de savoir d’où elles viennent, car on te demandera potentiellement de les démontrer si les matrices involutives tombent aux concours.
Première propriété
Soient \((A , B) \in \mathcal{M}_{n}(\mathbb{R})\) deux matrices involutives qui commutent, c’est-à-dire que \(AB = BA\) (ce qui n’est pas toujours le cas dans le cadre du produit matriciel ).
Alors : \((AB)^2 = (AB) \times (AB) = (AB) \times (BA) = A \times B^2 \times A = A \times I_n \times A = A ^2 = I_n,\)
d’où la matrice \(AB\) est bien une matrice involutive.
Deuxième propriété
Ici, c’est pratiquement du cours ! En effet, comme une matrice involutive vérifie l’égalité \(A^2 = I_n\), on en déduit que toute matrice involutive admet comme polynôme annulateur \(P : X \mapsto X^2 -1\)
Comme les valeurs propres d’une matrice sont des racines de son polynôme annulateur, on en déduit donc que le spectre de \(A\) est bien inclus dans {1 ; -1}.
Troisième propriété
Cette propriété concerne surtout les mathématiques approfondies, pour qui les matrices orthogonales sont au programme.
Ainsi, soit \(A \in \mathcal{M}_{n}(\mathbb{R})\) matrice involutive et symétrique. Alors, \({}^tAA = A^2 = I_n,\) d’où \({}^tA = A ^{-1},\) d’où \(A\) est une matrice orthogonale par définition.
Quatrième propriété
Pour démontrer cette propriété, une simple récurrence suffit. Soit \(P_n\) le prédicat suivant : « Si \(A\) est une matrice involutive alors \(A^n\) l’est également ».
Initialisation : pour n=0, on a bien \(A^0 = I_n\) une matrice involutive. En effet, \((I_n)^2 = I_n\)
Hérédité : supposons \(P_n\) vrai pour un certain \(n \in \mathbb{N} : A^{n+1} = A \times A^n.\)
Comme \(A\)et \(A^n\) sont deux matrices involutives (par hypothèse de récurrence) qui commutent, on en déduit d’après la première propriété que \(A^{n+1}\) est également une matrice involutive. \(P_{n+1}\) est donc vrai.
Conclusion : ainsi, si \(A\) est une matrice involutive, alors \(\forall n \in\mathbb{N}, A^n\) est une matrice involutive.
Cinquième propriété
La démonstration de cette propriété découle directement de la quatrième propriété. En effet, si \(A\) est une matrice involutive, on en déduit alors que \(\forall n \in\mathbb{N}, A^n\) est une matrice involutive. Dès lors, si \(n\) est pair, alors \(A^n = A^{2p} = (A^p)^2 = (I_n)^2 = I_n,\) avec en effet \(n=2p\), car pair et avec \(A^p\) une matrice involutive d’après la quatrième propriété.
Si \(n\) est impair, on peut écrire que \(n = {2p+1},\) d’où \(A^n = A^{2p+1} = A^{2p} \times A = I_n\times A = A.\)
Conclusion
La notion de matrice involutive est pour le moment tombée une seule fois aux concours, dans l’exercice 2 de Maths EDHEC ECS 1996.
N’hésite pas à consulter tous nos articles de mathématiques !