Les notions hors programme se destinent surtout aux candidats qui visent les trois Parisiennes. Cet article te propose de décortiquer la notion de matrice magique, assez récurrente dans les sujets de concours, pour mieux t’aider à comprendre avec des exemples, des schémas.
Tu retrouveras également une liste des propriétés intéressantes de cette notion afin d’être sensibilisé.e et ne pas être pris.e au dépourvu le jour J (cela te simplifiera la tâche pour ficher aussi).
La notion de matrice magique expliquée en français
Les matrices magiques sont des matrices telles que la somme de chaque ligne, chaque colonne, chaque diagonale et chaque antidiagonale soit la même. C’est tout simple !
Exemple concret d’une matrice magique
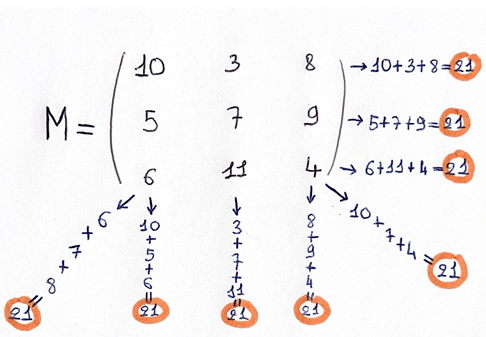
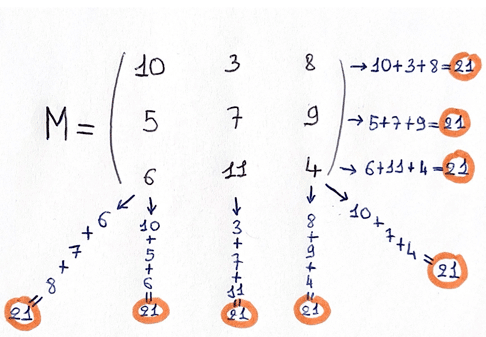
On considère la matrice \(M\) de \( \mathcal{M}_{3} (\mathbb{R}) \) suivante :
\[M=\begin{pmatrix}
10 & 3 & 8 \\
5 & 7 & 9 \\
6 & 11 & 4
\end{pmatrix}\]
On sait que cette matrice est dite magique, car :
Définition mathématique d’une matrice magique
Soit \(n \ge 3\)
Soit \(M \in \mathcal{M}_{n}(\mathbb{R}) \) tel que \(M=(m_{i,j})_{\underset{1 \le j \le n}{1 \le i \le n}}\)
\(M\) est une matrice magique lorsqu’elle vérifie les conditions suivantes :
- \(\forall i \in [\![1,n]\!], \ell_i(M)=\displaystyle \sum_{j=1}^n m_{i,j}\) (la somme des réels de la \(i\)ème ligne de \(M\) vaut le réel \(\ell_i(M)\)) ;
- \(\forall j \in [\![1,n]\!], c_j(M)=\displaystyle \sum_{i=1}^n m_{i,j}\) (la somme des réels de la \(j\)ème colonne de \(M\) vaut le réel \(c_j(M)\)) ;
- \(d_1(M)=\displaystyle \sum_{i=1}^n m_{i,i}\) (la somme des réels de la diagonale de \(M\) vaut le réel \(d_1(M)\), on remarque d’ailleurs que \(\text{Tr}(M)=d_1(M)\)) ;
- \(d_2(M)=\displaystyle \sum_{i=1}^n m_{i,n-i+1}\) (la somme des réels de l’antidiagonale de \(M\) vaut le réel \(d_2(M)\)).
On obtient donc la caractérisation d’une matrice magique
\(M\) est magique si et seulement si : \(\forall (i,j) \in [\![1,n]\!] \times [\![1,p]\!], \ell_i(M)=c_j(M)=d_1(M)=d_2(M)\) (toutes les dernières sommes sont égales entre elles).
On appelle parfois ce réel la constante magique.
On retrouve certaines variantes de la définition d’une matrice magique lorsque l’on pose une unique notation pour la constante magique notée \(s(M)\).
Dans ce cas, on aurait : \(\forall (i,j) \in [\![1,n]\!] \times [\![1,p]\!], s(M)=\ell_i(M)=c_j(M)=d_1(M)=d_2(M)\)
Donc, si on souhaite faire coller l’exemple à la définition pure, pour \(n=3\) :
- \(\forall i \in [\![1,3]\!], \ell_i(M)=\displaystyle \sum_{j=1}^3 m_{i,j}\), i.e.
\(\ell_1(M)=10+3+8=21 \)
\(\ell_2(M)=5+7+9=21\)
\(\ell_3(M)=6+11+4=21\) - \(\forall j \in [\![1,3]\!], c_j(M)=\displaystyle \sum_{i=1}^3 m_{i,j}\)
\(c_1(M)=10+5+6=21 \)
\(c_2(M)=3+7+11=21\)
\(c_3(M)=8+9+4=21\) - \(d_1(M)=\displaystyle \sum_{i=1}^3 m_{i,i}\)
\(d_1(M)=10+7+4=21 \) - \(d_2(M)=\displaystyle \sum_{i=1}^3 m_{i,3-i+1}\)
\(d_2(M)=6+7+8=21 \) - Comme on a bien \(\ell_1(M)=\ell_2(M)=\ell_3(M)=c_1(M)=c_2(M)=c_3(M)=d_1(M)=d_2(M)=21 \)
Alors, on en déduit que la matrice \(M\) est magique.
Quelques propriétés sur les matrices magiques
Soit \(n \ge 3\)
Soit \(M \in \mathcal{E}_n) \) tel que \(M=(m_{i,j})_{\underset{1 \le j \le n}{1 \le i \le n}}\)
- La matrice nulle est magique (ce qui est logique, car la constante magique sera égale à 0).
- \(\mathcal{E}_n\) est l’ensemble des matrices magiques. Il s’agit d’un sous-espace vectoriel de \(\mathcal{M}_{n}(\mathbb{R})\).
- Si \(M \in \mathcal{E}_n\), alors \({}^tM \in \mathcal{E}_n\) (la transposée d’une matrice magique reste magique, car le fait que les lignes et les colonnes soient échangées n’a aucune incidence sur la constante magique).
- Si \(s(M)\) est la constante magique, \(s\) est considérée comme une forme linéaire sur \(\mathcal{E}_n\), c’est-à-dire qu’il s’agit d’une application de l’ensemble \(\mathcal{E}_n\) vers l’ensemble des réels \(\mathbb{R}\) (c’est en cela qu’il s’agit d’une forme), application qui est en plus linéaire. De plus, il s’agit d’une application surjective, mais non injective.
- \(\mathcal{E}_n\) est stable pour le produit matriciel, c’est-à-dire que si l’on multiplie deux matrices magiques entre elles, la matrice produit des deux reste magique. On en déduit directement alors, du fait de la stabilité du \(\mathcal{E}_n\) pour le produit matriciel et du fait que \(s\) est une forme linéaire sur \(\mathcal{E}_n\) que : \( \forall (A,B) \in \mathcal{E}_n^2, s(AB)=s(A)s(B) \).
- Les exercices autour des matrices magiques font quasi systématiquement appel à la matrice \(J\) de \(\mathcal{M}_{n}(\mathbb{R})\) ayant tous ses coefficients égaux à 1 (on la note parfois \(J=(1)_{\underset{1 \le j \le n}{1 \le i \le n}}\)). En effet, elle est très pratique puisqu’on remarque que :
\(MJ=JM=s(M)J\). Donc, comme on a \(MJ=s(M)J\), avec \(J \neq 0\), alors \(s(M)\) est une valeur propre de \(M\) associée au vecteur propre \(J\). - L’inverse d’une matrice magique reste une matrice magique : \(M^{-1} \in \mathcal{E}_n\)
Et on a : \(s(M^{-1})=\frac{1}{s(M)}\).
Cas particulier de matrice magique : toutes les matrices magiques dont la constante magique est nulle
On note \(\mathcal{F}_n\) cet ensemble, il peut être écrit mathématiquement sous cette forme :
\(\mathcal{F}_n=\{M \in \mathcal{E}_n, s(M)=0 \}\)
\(\mathcal{F}_n\) est un sous-espace vectoriel de \(\mathcal{E}_n\)
En considérant la décomposition suivante (hors programme mais classique) :
\( \forall M \in \mathcal{M}_{n}(\mathbb{R}), \exists! (A,B) \in \mathcal{S}_{n} \times \mathcal{A}_{n}, M=A+B \) (avec \(\mathcal{S}_{n}\) l’ensemble des matrices symétriques de \(\mathcal{M}_{n}(\mathbb{R})\) et \(\mathcal{A}_{n}\) l’ensemble des matrices antisymétriques de \(\mathcal{M}_{n}(\mathbb{R})\))
Si \(M \in \mathcal{E}_n\), alors dans ce cas, on aura \((A,B) \in \mathcal{E}_{n}^2\).
- \(\text{Ker}(d)\) et \(\text{Vect}(J)\) sont deux sous-espaces vectoriels supplémentaires dans \(\mathcal{E}_n\) : \(\text{Ker}(d) \oplus \text{Vect}(J)=\mathcal{E}_n\)
- On a enfin : \(\text{dim}(\mathcal{E}_n)=(n-1)^2-1\)
Soit \((r,s) \in [\![2,n]\!]^2\)
Trouver la dimension de l’espace vectoriel des matrices magiques sera sans doute l’une des questions les plus techniques à faire du problème, car pour cela, il faudra trouver une base de \(\text{Ker}(d)\) qui est en fait la famille \((A_{r,s})_{(r,s) \in [\![2,n]\!]^2]}\) définie par la matrice : \(A_{r,s}=(a_{i,j}^{(r,s)})_{\underset{1 \le j \le p}{1 \le i \le n}}\) telle que :
• tous les coefficients sont nuls, sauf
• \(a_{1,1}^{(r,s)}=a_{r,s}^{(r,s)}=1\) et
• \(a_{1,s}^{(r,s)}=a_{r,1}^{(r,s)}=-1\)
N.B. : Cette question est technique, car il ne faut pas s’emmêler les pinceaux dans les notations !
On note \(A_{r,s}=(a_{i,j}^{(r,s)})_{\underset{1 \le j \le p}{1 \le i \le n}}\) en faisant apparaître les parenthèses \((r,s)\) au-dessus du coefficient \(a_{i,j}\), car on souhaite indiquer que l’on parle du coefficient n°\((i,j)\) de la matrice n° \((r,s)\) (puisqu’il y a plein de matrices qui sont toutes dans la famille \((A_{r,s})_{(r,s) \in [\![2,n]\!]^2}\). Chacune de ces matrices possède ses propres coefficients)
Exemple pour \(n=3\)
On a la famille \((A_{r,s})_{(r,s) \in [\![2,3]\!]^2}=(A_{2,2}, A_{2,3}, A_{3,2}, A_{3,3})\)
En particulier, prenons la matrice \(A_{2,3}\) (c’est donc une application du cas où \(r=2\) et \(s=3\)). Cette matrice possède tous ses coefficients nuls, sauf :
• \(a_{1,1}^{(2,3)}=a_{2,3}^{(2,3)}=1\) et
• \(a_{1,3}^{(2,3)}=a_{2,1}^{(2,3)}=-1\)
On a donc la matrice :
\(A_{2,3}=\begin{pmatrix}
1 & 0 & -1 \\
1 & 0 & -1 \\
0 & 0 & 0
\end{pmatrix}\)
Les sujets de concours avec la notion de matrice magique
Cette notion classique s’est retrouvée dans plusieurs annales de concours.
Tu pourras trouver les corrections de ces propriétés en cherchant dans ces ressources :
Tu peux aussi retrouver ici toutes nos autres ressources en maths.