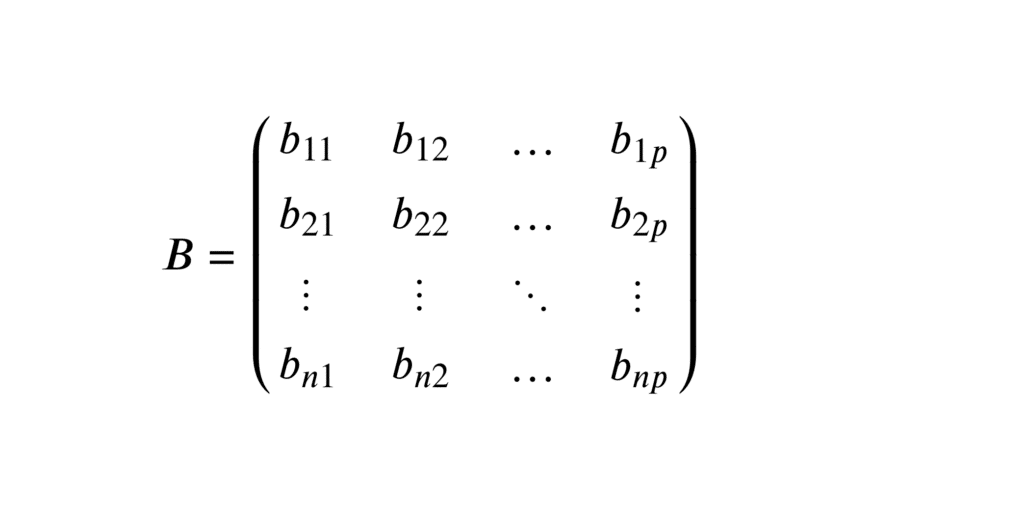On va travailler ensemble sur un thème essentiel en algèbre linéaire et au programme ECG, qui ne cesse de tomber chaque année aux concours : les matrices. Cet article a pour objectif de te présenter ce concept et surtout de te permettre de connaître et de comprendre tout ce qu’il faut savoir sur le thème des matrices.
Définition d’une matrice réelle à \( n \) lignes et \( p \) colonnes
Une matrice est un tableau rectangulaire de n lignes et de p colonnes constituées de nombres réels. On note souvent une matrice par une lettre majuscule. Chaque valeur située dans la matrice est appelée « élément de la matrice » et est notée par une lettre minuscule (correspondant à la lettre de la matrice) suivie de deux chiffres indiquant la ligne et la colonne de la valeur.
Par exemple, on prend une matrice B à \( n \) lignes et \( p \) colonnes. Chaque élément de la matrice sera noté par \( b_{ij} \), où \( i \) représente l’indice de la ligne et \( j \) celui de la colonne.
La matrice \( B \) se note donc :
\(
B = \begin{pmatrix}
b_{11} & b_{12} & \dots & b_{1p} \\
b_{21} & b_{22} & \dots & b_{2p} \\
\vdots & \vdots & \ddots & \vdots \\
b_{n1} & b_{n2} & \dots & b_{np}
\end{pmatrix}
\)
Quelques exemples de matrices à connaître
La matrice identité
La matrice identité, notée I, est une matrice carrée dont tous les éléments diagonaux sont tous égaux à \( 1 \) et tous les autres éléments sont nuls. Ainsi, on a :
\[ I_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}, \quad I_4 = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]
La matrice nulle
La matrice nulle désigne une matrice constituée uniquement de valeurs nulles, autrement dit de 0. Ainsi, on a : \[ 0_{2 \times 2} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}, \quad 0_{3 \times 3} = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \]
La matrice diagonale
Une matrice diagonale est une matrice carrée dont tous les éléments sont nuls, sauf les éléments de sa diagonale principale. Par exemple, la matrice \( A = \begin{pmatrix} 5 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 7 \end{pmatrix} \) est une matrice diagonale.
Les matrices symétriques et antisymétriques
Une matrice est dite symétrique si elle est égale à sa transposée, c’est-à-dire \( A = A^T \). Inversement, une matrice est dite antisymétrique si \( A^T = -A \). Ainsi, on a par exemple la matrice \( B = \begin{pmatrix} 4 & 1 & 2 \\ 1 & 5 & 3 \\ 2 & 3 & 6 \end{pmatrix} \) qui est une matrice symétrique, car :
\[ B^T = \begin{pmatrix} 4 & 1 & 2 \\ 1 & 5 & 3 \\ 2 & 3 & 6 \end{pmatrix} = B \]
Les matrices triangulaires
Une matrice est triangulaire supérieure si tous les éléments en dessous de sa diagonale principale sont nuls. Inversement, une matrice est triangulaire inférieure si tous les éléments au-dessus de sa diagonale principale sont nuls, telle que : \[ U = \begin{pmatrix} 1 & 2 & 4 \\ 0 & 3 & 5 \\ 0 & 0 & 6 \end{pmatrix} \]
De nombreuses autres matrices existent, notamment la matrice Atilla (constituée uniquement de 1) qui, bien que hors programme, apparaît très régulièrement dans les sujets de concours.
Les opérations élémentaires sur les matrices
Additionner/soustraire des matrices
Deux matrices peuvent être additionnées/soustraites si et seulement si elles sont de la même dimension (même nombre de lignes et de colonnes). Le résultat de l’addition de deux matrices de dimension \( m \times n \) est une nouvelle matrice de dimension \( m \times n \). On obtient ce résultat en additionnant les éléments correspondants de chaque matrice. Ainsi, soit deux matrices \( A \) et \( B \) de dimensions \( 2 \times 2 \) :
\( A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \quad B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} \)
L’addition de ces deux matrices donne la matrice \( C = A + B \) :
\( C = A + B = \begin{pmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{pmatrix} = \begin{pmatrix} 6 & 8 \\ 10 & 12 \end{pmatrix} \)
De plus, il y a commutativité et associativité lors de calcul des matrices. Autrement dit :
- \( A + B = B + A \)
- \( (A+B)+C=A+(B+C) \)
La soustraction de deux matrices se fait sous les mêmes conditions et de la même manière.
Multiplier des matrices
On peut calculer le produit de deux matrices si et seulement si le nombre de colonnes de la première matrice est égal au nombre de lignes de la seconde matrice.
\( \displaystyle c_{ij} = \sum_{k=1}^{n} a_{ik} b_{kj} = a_{i1} b_{1j} + a_{i2} b_{2j} + \cdots + a_{in} b_{nj} \)
Il y a associativité, distributivité, lors de multiplication des matrices mais, le plus souvent, non-commutativité. Autrement dit :
- \( A \times (B \times C) = (A \times B) \times C \)
- \( A \times (B + C) = A \times B + A \times C \)
- \( A \times B \neq B \times A \)
Dans le même style, tu peux jeter un œil à cet excellent article qui te livre des astuces sur les matrices.
La transposition de matrices
La transposition d’une matrice consiste en l’inversion de ses lignes et de ses colonnes ensemble. Autrement dit, on va prendre les éléments formant les lignes de la matrice pour les transformer en éléments des colonnes de cette matrice.
Si \( A \) est une matrice de taille \( m \times n \) (c’est-à-dire que \( A \) a \( m \) lignes et \( n \) colonnes), alors sa transposée \( A^T \) est une matrice de taille \( n \times m \).
Prenons, par exemple, la matrice \( A \) de taille \( m \times n \), telle que \[ A = \begin{pmatrix} 2 & 5 & 7 \\ 3 & 6 & 1 \\ 4 & 8 & 9 \end{pmatrix} \]
Alors, la transposée \( A^T \) est obtenue en échangeant les lignes et les colonnes de \( A \). On a donc : \[ A^T = \begin{pmatrix} 2 & 3 & 4 \\ 5 & 6 & 8 \\ 7 & 1 & 9 \end{pmatrix} \]
La partie 3 du dernier sujet Maths II appliquées ESSEC de 2024 mettait particulièrement en jeu le concept de transposition.
Comment trouver le déterminant d’une matrice ?
Le déterminant d’une matrice (A) se note \( \det(A) \) et désigne une valeur scalaire permettant de connaître les propriétés d’une matrice, en particulier son inversibilité. Le déterminant d’une matrice est défini uniquement pour les matrices carrées, autrement dit de tailles \( n \times n \), où \( n \) est un entier positif.
Pour les matrices de taille \( 2 \times 2 \) telle que \( A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \), le déterminant s’obtient en réalisant le calcul suivant :
\( \det(A) = ad – bc \)
Pour les matrices de taille \( 3 \times 3 \) telle que \( A = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}, \) le déterminant s’obtient en réalisant le calcul suivant :
\( \det(A) = a(ei – fh) – b(di – fg) + c(dh – eg). \)
Pour les matrices de tailles \( n \times n \), le calcul manuel est souvent fastidieux, alors il te sera peut-être plus souvent demandé d’utiliser, sur Python, la formule de la bibliothèque numpy: np.linalg.det (A).
Mais tu peux aussi retenir deux propriétés (simples) qui te permettent de trouver le déterminant :
- Si deux lignes/colonnes d’une matrice sont proportionnelles, ou si une matrice contient une ligne/colonne de zéros, le déterminant est également nul.
- Le déterminant d’une matrice triangulaire est le produit des éléments de la diagonale.
Comment calculer le rang d’une matrice ?
Le rang d’une matrice est défini comme le nombre maximal de vecteurs lignes ou colonnes linéairement indépendants dans cette matrice. Le rang représente aussi la dimension de l’espace vectoriel formé par les vecteurs lignes ou colonnes de la matrice.
Concernant les techniques de calcul du rang d’une matrice, je te propose de lire cet excellent article qui présente en détail toutes les méthodes pour calculer le rang d’une matrice.
Mais tu peux aussi utiliser en Python, et grâce à la bibliothèque numpy, la formule np.linalg.matrix.rank (la matrice proposée) qui renvoie le rang de la matrice proposée.
Trouver l’inverse d’une matrice
Une matrice est inversible si et seulement si son déterminant est non nul. Si le déterminant est nul, la matrice est dite singulière et ne peut pas être inversée. L’inverse d’une matrice \( A \) est noté \( A^{-1} \). L’inverse d’une matrice désigne la matrice qui, lorsqu’elle est multipliée par \( A \), donne la matrice identité \( I \). Autrement dit, \( A \times A^{-1} = A^{-1} \times A = I \), où \( I \) est la matrice identité.
Pour une matrice de taille \( 2 \times 2 \) telle que \( A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \), la matrice est inversible si \( \det(A) = ad – bc \neq 0 \). Alors, l’inverse de cette matrice est donné par : \[ A^{-1} = \frac{1}{\det(A)} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \]
Pour les matrices de taille \( n \times n \), on utilise généralement l’élimination de Gauss-Jordan. Cette méthode est assez proche du pivot de Gauss. L’élimination de Gauss-Jordan consiste à mettre côte à côte la matrice de départ et une matrice identité de départ. On réalise alors des opérations élémentaires sur la matrice de départ afin de la transformer en matrice identité. Ces mêmes opérations sont appliquées à la matrice identité de départ, et la matrice finale obtenue correspond à la matrice inverse.
Diagonalisation d’une matrice et valeurs propres
Une matrice \( A \) de taille \( n \times n \) est diagonalisable si, et seulement si, il existe une matrice inversible \( P \) et une matrice diagonale \( D \) telles que : \[ A = P D P^{-1} \]
On diagonalise des matrices afin de faciliter l’étude de ces dernières, notamment car \( \forall n \in \mathbb{N}, \quad A_n = P D_n P^{-1} \)
Les éléments de la matrice \( D \) sont les valeurs propres de \( A \). Les valeurs propres de \( A \) désignent les valeurs \( \lambda \) telles qu’il existe un vecteur \( x \) non nul tel que : \[ A \mathbf{x} = \lambda \mathbf{x} \]
Pour qu’une valeur \( \lambda \) soit valeur propre de A , il faut que la matrice \( A – \lambda I \) soit non inversible. Autrement dit, pour trouver les valeurs propres de A, il faut que le déterminant de la matrice \( A – \lambda I \) soit nul. On réalise donc le calcul suivant :
\[
\text{det}(A – \lambda I) = 0
\]
Je te laisse lire ce super article pour découvrir toutes les techniques de diagonalisation et d’identification des valeurs propres.
Matrice et langage Python
Les sujets de concours faisant de plus en plus intervenir des exercices avec du Python, il est indispensable de connaître un certain nombre de formules dans ce langage concernant les matrices. La majorité de ces formules se trouvent dans la bibliothèque numpy (n’oublie pas de toujours l’importer en début de programme). Je te mets déjà une liste (non exhaustive) ci-dessous :
- np.array ([[1, 2], [3, 4]]) : permet de définir la matrice \( A = \begin{pmatrix}
1 & 2 \\
3 & 4
\end{pmatrix}
\) - np.dot(A, B) : permet de multiplier deux matrices A et B
- np.linalg.matrix_power(A, 3) : permet d’élever une matrice à la puissance donnée. Ici \(A^3 \)
- np.linalg.inv(A) : renvoie l’inverse de la matrice A
- np.linalg.det(A) : donne le déterminant de la matrice A
- np.linalg.eig(A) : renvoie les valeurs propres et les vecteurs propres de A
- np.linalg.matrix_rank(A) : permet d’obtenir le rang de la matrice A
Exemple d’expression du produit de deux matrices en langage Python
Il est indispensable de maîtriser cette question facile, mais pourtant très récurrente dans les sujets EDHEC/emlyon, car elle te fera gagner de précieux points aux concours. Reprenons alors les matrices \( A \) et \( B \) définies au début de l’article et écrivons ensemble le produit de ces matrices en langage Python pour obtenir la matrice \( D \) :
<spandata-mce-type=”bookmark” style=”display: inline-block; width: 0px; overflow: hidden; line- height: 0;” class=”mce_SELRES_start”>
Conclusion
Tu connais maintenant tout ce qu’il faut savoir sur les matrices. Tu es désormais capable de donner une définition claire de ce qu’est une matrice et quelques exemples particuliers, de multiplier des matrices, mais aussi d’en trouver l’inverse et de les diagonaliser. Tu es même capable d’écrire le produit de matrices sur Python !
J’espère que cet article t’a plu. Tu peux retrouver ici toutes nos autres ressources mathématiques et continuer à t’exercer sur d’autres annales grâce à notre méga-répertoire.