Les notions hors programme se retrouvent surtout dans les sujets de mathématiques destinés à l’intégration des trois Parisiennes. Ces explications s’adressent donc principalement aux candidat·e·s souhaitant se préparer à ces épreuves. Cet article met en lumière la notion de matrices par blocs, en l’expliquant par des définitions ainsi que des schémas.
Tu pourras également retrouver toutes les propriétés associées à cette notion pour être préparé·e le jour où tu la rencontreras !
La notion de matrice par blocs expliquée en français
Une matrice par blocs est une matrice carrée décomposée en sous-matrices, appelées blocs, qui sont alors toutes mises « les unes à côté des autres » pour former cette grande matrice carrée.
Toutes les sous-matrices sont donc de dimension inférieure à la matrice principale, et la matrice paraît découpée avec des lignes verticales et horizontales qui la traversent.
Exemple concret d’une matrice par blocs
Prenons la matrice \(P=\begin{pmatrix} 1 & 1 & 2 & 2 & 2 \\ 1 & 1 & 2 & 2 & 2 \\ 3 & 3 & 4 & 4 & 4 \\ 3 & 3 & 4 & 4 & 4 \\ 3 & 3 & 4 & 4 & 4 \end{pmatrix}\).
Nous pouvons alors la diviser en quatre sous-matrices :
\[P_{1,1}=\begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}, P_{1,2}=\begin{pmatrix} 2 & 2 & 2 \\ 2 & 2 & 2 \end{pmatrix}, P_{2,1}=\begin{pmatrix} 3 & 3 \\ 3 & 3 \\ 3 & 3 \end{pmatrix}, P_{2,2}=\begin{pmatrix} 4 & 4 & 4 \\ 4 & 4 & 4 \\ 4 & 4 & 4 \end{pmatrix}\]
Ainsi, \(P=\begin{pmatrix} P_{1,1} & P_{1,2} \\ P_{2,1} & P_{2,2} \end{pmatrix}\).
Les différents blocs des matrices ne peuvent donc pas être de n’importe quelle dimension. Si le premier bloc en haut à droite est de dimension 2×2, alors tous les blocs en dessous auront deux colonnes chacun (mais leur nombre de lignes sera quelconque). Et tous les blocs à côté (qui seront sur les mêmes lignes) auront deux lignes (mais un nombre de colonnes quelconque).
Définition mathématique d’une matrice par blocs
Dans la théorie des matrices, une matrice par blocs, appelée aussi matrice partitionnée, est une matrice divisée en sous-matrices rectangulaires, appelées blocs, en commençant par la division de sa diagonale. Les différents blocs doivent cependant être cohérents en termes de colonnes et de lignes :
- on groupe les lignes pour en faire des groupes dits adjacents ;
- on fait de même pour les colonnes ;
- la plupart des partitions font en sorte que les blocs de la diagonale soient carrés.
Ainsi, la matrice est divisée en rectangles obtenus par des groupes de lignes adjacentes croisant des groupes de colonnes adjacentes (elle est donc découpée par des lignes horizontales et verticales qui la traversent).

Quelques propriétés des matrices par blocs
Soit \((n,m,p) \in \mathbb N^3\).
Soient \(A\in\mathcal{M}_{m,p}(\mathbb{R})\) et \(B\in\mathcal{M}_{p,n}(\mathbb{R})\) deux matrices par blocs (utilisées pour la multiplication), et soient \(M\in\mathcal{M}_{m,n}(\mathbb{R})\) et \(N\in\mathcal{M}_{p,q}(\mathbb{R})\) (utilisées pour les sommes et produits directs) :
- multiplication de deux matrices par blocs : soit \(C\in\mathcal{M}_{m,n}(\mathbb{R})\) telle que \(C=AB\). Supposons que \(A\) et \(B\) soient deux matrices par blocs, partitionnées en \(q\) lignes et \(s\) colonnes pour \(A\) et en \(s\) lignes et \(r\) colonnes pour \(B\). Pour calculer \(C\) par blocs, il suffit de faire le calcul suivant (en sachant que chaque bloc de \(A\) doit contenir le même nombre de colonnes que le nombre de lignes pour chaque bloc correspondant de \(B\)) : \[C_{i,j}=\displaystyle\sum_{k=1}^{s}A_{i,k}B_{k,j}\] avec \(i\in[\![1,q]\!]\) et \(j\in[\![1,r]\!]\). \(C\) est donc composée de \(i\times j\) blocs, que l’on calcule grâce aux blocs de \(A\) et de \(B\).
- Somme directe de deux matrices par blocs : il existe une somme directe de \(M\) et \(N\), notée \(M\oplus N\) définie par \[M\oplus N=\begin{pmatrix} m_{1,1} & \ldots & m_{1,n} & 0 & \ldots & 0 \\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ m_{m,1} & \ldots & m_{m,n} & 0 & \ldots & 0 \\ 0 & \ldots & 0 & n_{1,1} & \ldots & n_{1,q} \\ \vdots & \ldots & \vdots & \vdots & \ldots & \vdots \\ 0 & \ldots & 0 & n_{p,1} & \ldots & n_{p,q} \end{pmatrix}\] La matrice obtenue contient donc quatre blocs, le bloc représentant la matrice \(M\), celui de la matrice \(N\) et deux blocs ne contenant que des 0.
- Produit direct dit produit de Kronecker : il existe également un produit direct de deux matrices \(M\) et \(N\), noté \(M \otimes N\), défini par \[M \otimes N=\begin{pmatrix} m_{1,1}N & \ldots & m_{1,n}N \\ \vdots & \ddots & \vdots \\ m_{m,1}N & \ldots & m_{m,n}N\end{pmatrix}\] La matrice obtenue contient donc \(m \times n\) blocs, qui correspondent à la matrice \(N\) multipliée par chaque coefficient de la matrice \(M\).
Zoom sur les matrices par blocs diagonales
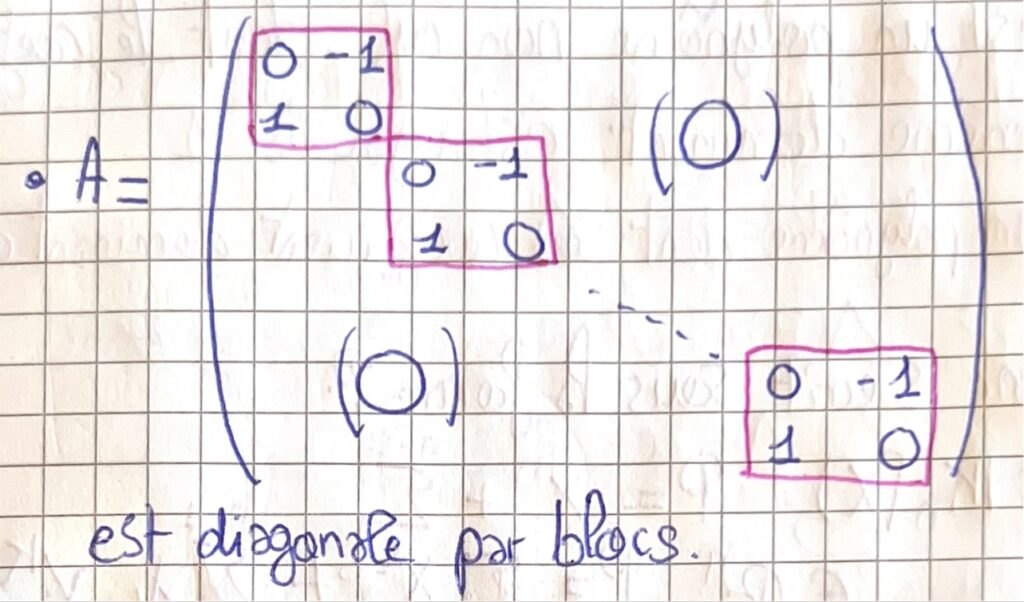
Posons \(A\in\mathcal{M}_{m,n}(\mathbb{R})\) une matrice carrée qui possède \(p\) blocs matrices carrées sur sa diagonale, et uniquement des blocs matrices nulles ailleurs. On a alors : \[A=\begin{pmatrix} A_1 & 0 & \ldots & 0 \\ 0 & A_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & A_p\end{pmatrix}\] ou les \(A_k\) sont des matrices carrées.
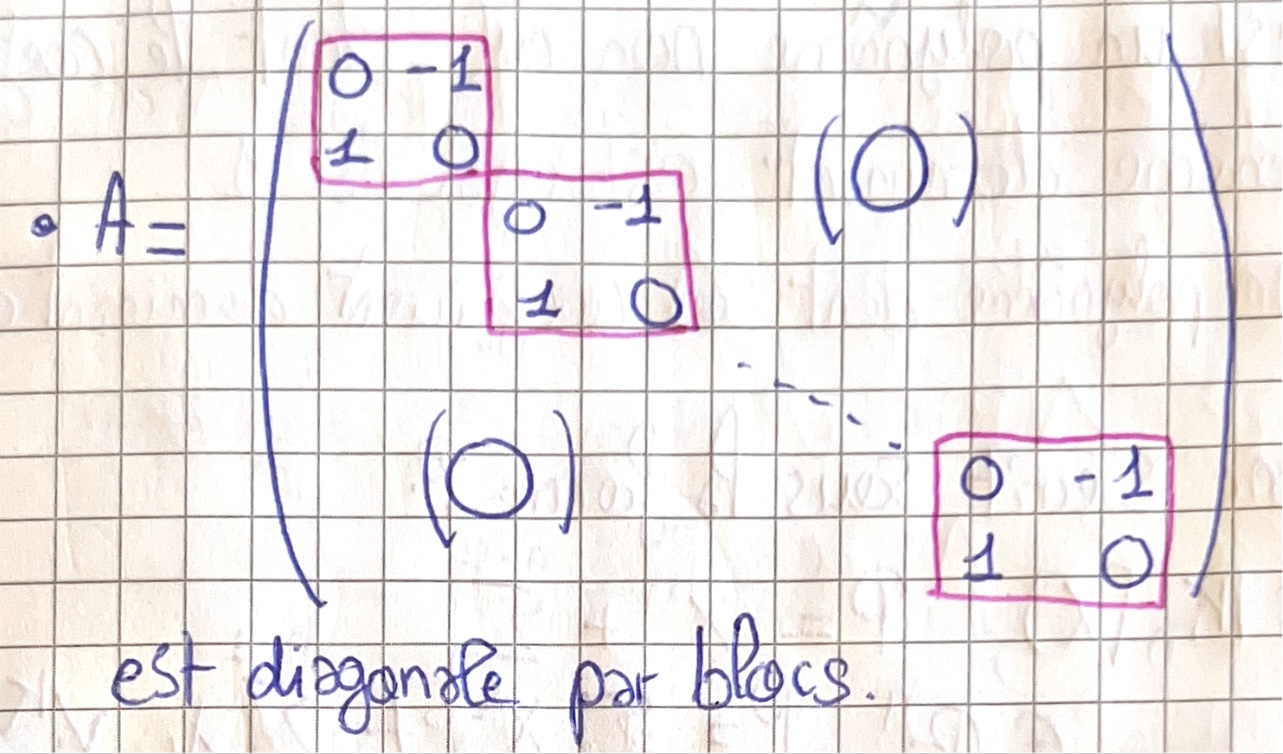
- D’après la définition de la somme directe, \(A=A_1 \oplus A_2 \oplus \ldots \oplus A_p\).
- On obtient également que \(det(A)=det(A_1) \times \ldots \times det(A_p)\) et que \(Tr(A)=Tr(A_1) + \ldots + Tr(A_p)\).
- La transposée de \(A\) est la somme directe de chaque transposée des \(A_k\), c’est-à-dire que \[{}^tA=\begin{pmatrix} {}^tA_{1} & 0 & \ldots & 0 \\ 0 & {}^tA_{2} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & {}^tA_{p}\end{pmatrix}\]
- C’est la même chose pour calculer \(A^i\), pour tout \(i\in\mathbb{N}^{*}\), on obtient que \[A^i=\begin{pmatrix} A_{1}^{i} & 0 & \ldots & 0 \\ 0 & A_{2}^{i} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & A_{p}^{i}\end{pmatrix}\]
- Enfin, pour l’inverse de \(A\), le calcul est le même : \[A^{-1}=\begin{pmatrix} A_{1}^{-1} & 0 & \ldots & 0 \\ 0 & A_{2}^{-1} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & A_{p}^{-1}\end{pmatrix}\]
Les sujets de concours avec la notion de matrices par blocs
Cette notion hors programme se retrouve dans certains sujets de concours. En voici la liste non exhaustive avec les corrections ci-jointes.
- L’exercice 1.62 des oraux HEC 2017
- HEC 2016
- ESSEC 2020
- ESSEC 2011