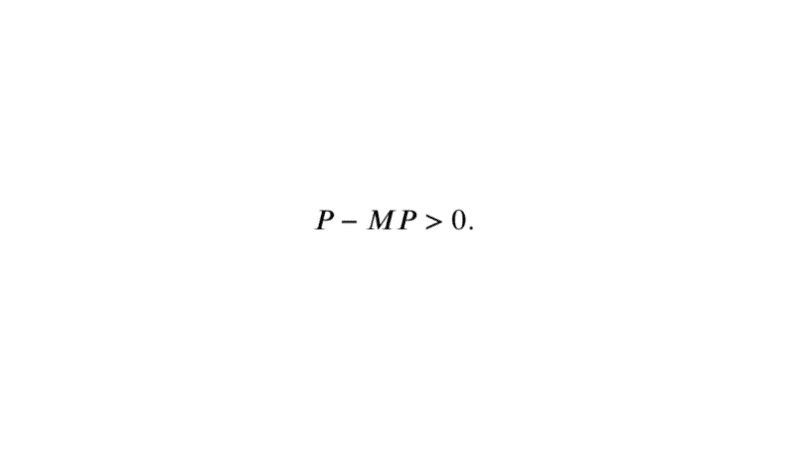On se retrouve pour étudier une notion hors programme bien intéressante : les matrices productives. C’est donc l’occasion pour toi d’approfondir ta maîtrise de l’algèbre, tout en ayant un coup d’avance si cette notion (re)tombe aux concours.
Définition d’une matrice productive
Pour comprendre le concept de matrice productive, il faut avant tout comprendre les notions de matrice positive et de matrice strictement positive.
Soit \(\mathcal{M}_{n}(\mathbb{R})\) l’ensemble des matrices carrées réelles d’ordre \(n,\) et soit \(\mathcal{M}_{n,1}(\mathbb{R})\) l’ensemble des matrices colonnes réelles à \(n\) lignes. Une matrice \(M\) qui appartient à\(\mathcal{M}_{n}(\mathbb{R})\) ou à \(\mathcal{M}_{n,1}(\mathbb{R})\) est dite positive si et seulement si tous ses coefficients sont positifs ou nuls. On notera alors \(M \ge 0.\)
Une matrice \(M\) qui appartient à\(\mathcal{M}_{n}(\mathbb{R})\) ou à \(\mathcal{M}_{n,1}(\mathbb{R})\) est dite strictement positive si et seulement si tous ses coefficients sont strictement positifs. On notera alors \(M > 0.\)
\[\fbox{Dès lors, une matrice \(M\in \mathcal{M}_{n}(\mathbb{R})\) est dite productive si et seulement si \(M\) est positive et \(\exists P \in \mathcal{M}_{n,1}(\mathbb{R}),\) telle que \(P-MP > 0.\)}\]
Un premier exemple
Pour comprendre la notion de matrice productive, prenons un exemple simple
Soit \(A =\displaystyle \frac{1}{3} \begin{pmatrix} 0 & 1 & 1\\ 1 & 0 & 1 \\ 1 & 1 & 0\end{pmatrix}\)
Premièrement, \(A\) est bien une matrice positive, car tous ses coefficients sont positifs ou nuls. De plus, en considérant \(U= \begin{pmatrix} 1\\ 1 \\ 1\end{pmatrix},\) qui est bien une matrice colonne positive, on obtient que :
\[U-AU = \begin{pmatrix} 1\\ 1 \\ 1\end{pmatrix} – \displaystyle \frac{1}{3}\begin{pmatrix} 0 & 1 & 1\\ 1 & 0 & 1 \\ 1 & 1 & 0\end{pmatrix}\begin{pmatrix} 1\\ 1 \\ 1\end{pmatrix} = \begin{pmatrix} 1\\ 1 \\ 1\end{pmatrix} – \displaystyle \frac{1}{3}\begin{pmatrix} 2\\ 2 \\ 2\end{pmatrix} = \displaystyle \frac{1}{3}\begin{pmatrix} 1\\ 1 \\ 1\end{pmatrix} > 0\]
Ainsi \(A\) est bien une matrice productive.
À l’inverse, on peut également montrer qu’une matrice n’est pas productive
Par exemple, soit \(B =\begin{pmatrix} 1 & 4 & 1\\ 2 & 1 & 3 \\ 0 & 0 & 1\end{pmatrix}\)
On remarque dans un premier temps que \(B\) est bien une matrice positive, condition nécessaire à la définition d’une matrice productive. Maintenant, soit \(X=\begin{pmatrix} x\\y\\z\end{pmatrix},\) une matrice colonne positive. On obtient par le calcul :
\(X – BX = \begin{pmatrix} x\\y\\z\end{pmatrix} – \begin{pmatrix} 1 & 4 & 1\\ 2 & 1 & 3 \\ 0 & 0 & 1\end{pmatrix}\begin{pmatrix} x\\y\\z\end{pmatrix} = \begin{pmatrix} x\\y\\z\end{pmatrix} – \begin{pmatrix} x + 4y + z\\2x + y + 3z\\z\end{pmatrix} = \begin{pmatrix} -4y – z\\-2x – 3z\\0\end{pmatrix}.\)
Comme le dernier coefficient de \(X – BX\) est nul, on en déduit que cette matrice colonne n’est pas strictement positive. Il est donc impossible de trouver une matrice colonne \(P\) satisfaisant la condition \(P-BP > 0 : B\) n’est donc pas productive par définition.
Propriétés principales des matrices productives
Désormais, intéressons-nous aux principales propriétés concernant les matrices productives. Si ces propriétés ne sont pas nécessairement à connaître par cœur, c’est sans doute celles-ci qu’on te demandera de démontrer dans le cadre d’un exercice sur les matrices productives aux concours.
\[\fbox{Soit \(A\) une matrice productive de \(\mathcal{M}_{n}(\mathbb{R})\) et \(P\) une matrice positive telle que \(P-AP > 0.\) Alors, on a : \(P > 0\)}\]
\[\fbox{Une matrice \(A\in\mathcal{M}_{n}(\mathbb{R})\) est productive si et seulement si : \(A\) est positive, \(I_n – A\) est inversible, et \((I_n -A)^{-1}\) est positive.}\]
\[\fbox{Soit \(A\) une matrice productive. Alors, \({}^tA\) est également productive.}\]
Démonstrations intéressantes de ces propriétés
Première propriété
La démonstration de la première propriété s’appuie sur le résultat suivant :
\[\fbox{Si \(M\) est une matrice positive, alors \(\forall X \in \mathcal{M}_{n,1}(\mathbb{R})\) est positive, \(MX\) est une matrice positive.}\]
Ce résultat est assez simple à démontrer, je t’invite à regarder la deuxième partie du problème 2 de Maths EM Lyon ECS 2004 qui en propose une démonstration.
Une fois ce résultat admis, on peut commencer à se pencher sur la propriété qui nous intéresse.
Posons \(W = AP = \begin{pmatrix} w_{1} \\ w_{2} \\ \vdots \\ w_{n} \end{pmatrix}.\) Alors, \(T = P – AP = \begin{pmatrix}p_{1} – w_{1} \\ p_{2} – w_{2} \\ \vdots \\ p_{3} – w_{n} \end{pmatrix}\)
Comme \(A\) est supposée productive, on a donc que \(T > 0,\) d’où \(\forall i \in [\![1,n]\!], p_{i} – w_{i} > 0,\)d’où \(\forall i \in [\![1,n]\!], p_{i} > w_{i}.\)
\(A \) étant productive, cette matrice est positive par définition d’une matrice productive : \(P\) étant (strictement) positive, on en déduit que \(W = AP\) est bien positive selon la propriété que nous avons admise juste au-dessus.
Dès lors, \(\forall i \in [\![1,n]\!], p_{i} > w_{i} \ge 0,\)d’où \(\forall i \in [\![1,n]\!], p_{i} > 0 :\) on en déduit par définition que \(P > 0.\)
Deuxième propriété
Je ne vais pas détailler ici l’entièreté de la démonstration, car cela peut être l’objet de toute une partie d’un problème. Ce fut notamment le cas dans le second problème de Maths EM Lyon 2004 ECS, que je t’invite à étudier, car c’est à ce jour la seule fois que les matrices productives sont tombées aux concours.
Troisième propriété
Cette démonstration utilise directement la deuxième propriété.
Soit \(A\) une matrice productive : alors d’après la deuxième propriété, on sait que \(A\) est positive, \(I_n – A\) est inversible, et \((I_n -A)^{-1}\) est positive. On sait, dans un premier temps, que si \(A\) est une matrice productive, alors, si l’on note \(A = (a_{i,j})_{1 \le i,j \le n}\) et \({}^tA=(b_{i,j})_{1 \le i,j \le n},\forall (i,j) \in [\![1,n]\!]^2, b_{i,j} = a_{j,i} \ge 0\), car \(A\) est une matrice positive, donc \({}^tA\) est également positive.
De plus, comme \(A\) est une matrice productive, on sait que \((I_n -A)^{-1}\) existe, et donc sa transposée existe :
\({}^t((I_n -A)^{-1}) = ({}^t(I_n -A))^{-1} = (I_n -{}^tA))^{-1}\)
D’où l’inverse de \(I_n – {}^tA\) existe bien.
Enfin, comme on sait que la transposée d’une matrice positive est positive, on sait que \(((I_n -{}^tA))^{-1} = {}^t((I_n -A)^{-1}) \ge 0\)
Ainsi, \({}^tA\) est positive, \(I_n – {}^tA\) est inversible, et \((I_n -{}^tA)^{-1}\) est positive, d’où, d’après la deuxième propriété que nous avons mise en évidence, \({}^tA\) est une matrice productive.
Conclusion
La notion de matrice productive est pour le moment tombée une seule fois au concours, dans le problème de Maths EM Lyon ECS 2004.
N’hésite pas à consulter tous nos articles de mathématiques !