Tu connais tes méthodes classiques pour montrer qu’une série à termes positifs converge (équivalent, petit \(\mathcal{o}\), majoration), mais sais-tu qu’il en existe une autre qui tombe fréquemment aux écrits et beaucoup aux oraux ? Cette méthode se nomme la méthode de la comparaison entre une série et une intégrale, et elle est très souvent utilisée pour déterminer l’équivalent d’une somme. Bien que très efficace, l’application de cette méthode demande beaucoup de rigueur et la vérification de certaines hypothèses, souvent négligées. Dans cet article, on verra tout ce qu’il faut savoir sur cette méthode !
La comparaison série-intégrale
L’idée de la méthode est d’encadrer la somme d’intérêt à l’aide d’intégrales qui faciliteront par la suite le calcul numérique du minorant et du majorant à l’aide notamment des propriétés sur les sommes télescopiques.
Explication de la méthode
Pour expliquer la méthode de façon générale, je vais étudier le cas particulier que représente la série \(\displaystyle \underset{n\ge 1}{\sum}\frac{1}{\sqrt{n}}\), afin d’obtenir un équivalent simple de la somme \(\displaystyle \sum_{k=1}^n\frac{1}{\sqrt{k}}\) au voisinage de \(+\infty\), par exemple \(e^n\), \(\sqrt{n}\), bref, des quantités définies par des produits, quotients de quantités usuelles.
Je vais noter cette expression que l’on cherche : \(\text{truc}_{\text{simple}}(n)\), telle que : \[\sum_{k=1}^n \frac{1}{\sqrt(k)} \underset{n \rightarrow + \infty}{\sim} \text{truc}_{\text{simple}}(n)\]Avant toute chose, la fonction \(\displaystyle f:x\mapsto \frac{1}{\sqrt{x}}\) est une fonction continue, positive et décroissante sur \(]0, +\infty[\).
La vérification de ces hypothèses est essentielle, étant donné que la continuité de \(f\) est nécessaire dans la manipulation des intégrales. De plus, la fonction doit vérifier : \(\forall x\in ]0, +\infty[, f(x) \ge 0\) (positivité), sinon la relation d’ordre précisée ci-dessous ne serait pas forcément vérifiée si certaines aires sont négatives. Enfin, dès que l’on a la positivité de la fonction, la nécessité de la décroissance est évidente, sinon la relation d’ordre ne pourrait être vérifiée, et donc on ne pourrait pas comparer les quantités nécessaires à la comparaison série-intégrale.
Notons qu’il existe des cas où l’on travaille avec une fonction qui est cette fois-ci croissante, la méthode reste similaire, toutefois ces cas ne sont vraiment pas monnaie courante, étant donné qu’ils ont un intérêt moindre puisque le terme général ne pourra jamais tendre vers zéro (pour des fonctions positives), et donc la série divergera grossièrement.
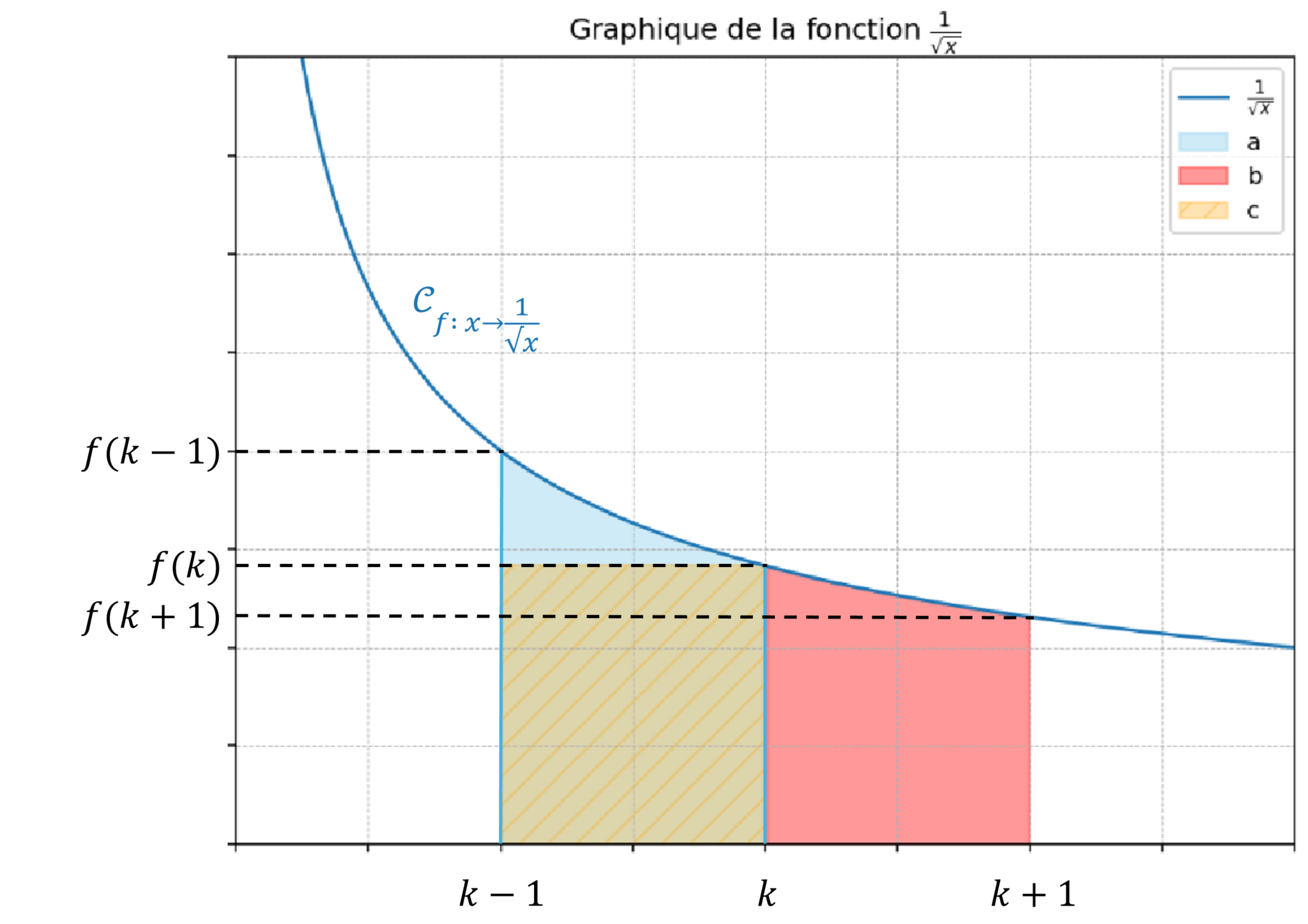
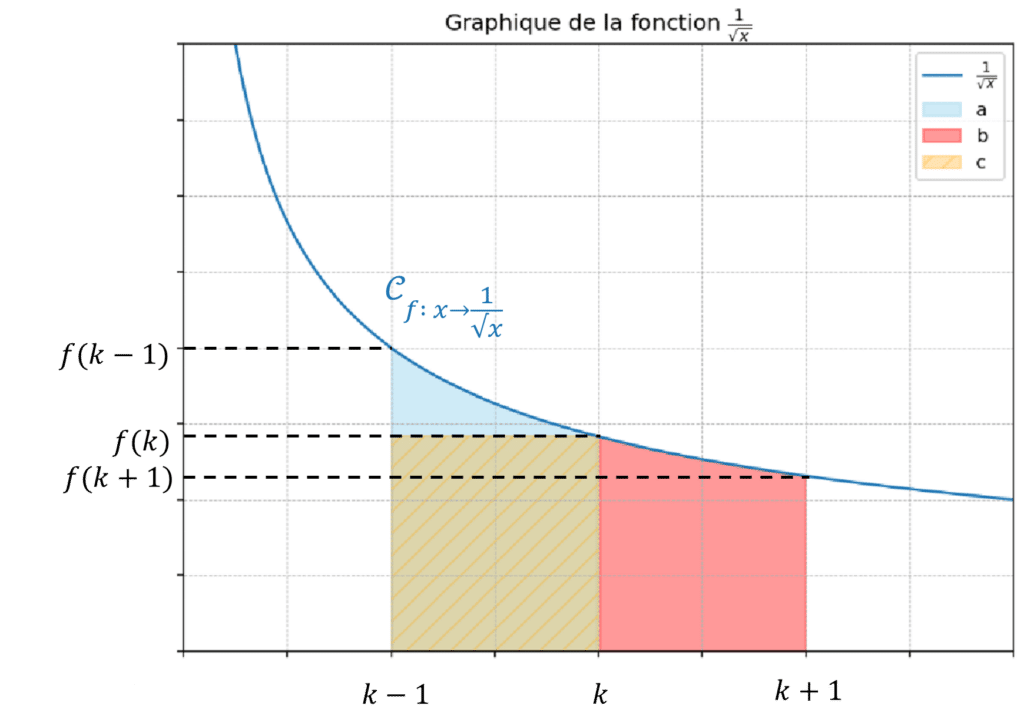
La méthode consiste dans un premier temps à tracer le graphe du terme général, à y figurer les aires sous les courbes délimitées par les segments \([k-1, k]\)(en bleu), et \([k, k+1]\) (rouge), et à les comparer par rapport à l’aire sous la courbe de la fonction constante \(x\mapsto f(k)\) délimitée par le segment \([k-1,k]\) (en vert hachuré), avec \(k\) appartenant à un intervalle pertinent.
Puis on traduit la comparaison graphique en langage mathématique. Ensuite, on détermine une expression mathématique simple des aires en rouge et en bleu (en intégrant, sous réserve que la primitive soit calculable, ce qui sera très souvent le cas).
Vient le moment de sommer les inégalités, ce qui fait apparaître la somme dont on veut trouver l’équivalent. Et ceci étant fait, on simplifie l’encadrement à l’aide des propriétés sur les sommes télescopiques notamment.
Il ne reste désormais plus qu’à trouver une fonction adéquate qui permet, après passage à la limite, d’obtenir un équivalent de la somme, par le théorème d’encadrement.
Mettons en évidence qu’il existe d’autres méthodes d’encadrement qui suivent le même principe que la comparaison série-intégrale : la méthode des rectangles et la méthode des trapèzes.
Mise en place de l’encadrement
D’une part, graphiquement, on observe que :
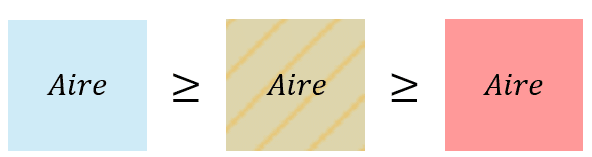
Ce qui donne mathématiquement : \[\int_{k-1}^k f(x)\text{d}x \ge f(k)\times 1 \ge \int_k^{k+1} f(x)\text{d}x\]
Soit :
\(\displaystyle \forall k\ge 2, \int_{k-1}^k \frac{1}{\sqrt{x}}\text{d}x\ge f(k)\), et : \(\displaystyle \forall k\ge 1, \int_k^{k+1} \frac{1}{\sqrt{x}}\text{d}x\le f(k)\).
La disjonction de cas selon la valeur de \(k\) est nécessaire, sinon l’intégrale de gauche ne serait pas définie si \(k\) était égale à \(1\), par exemple.
Comme une primitive de \(\displaystyle x\mapsto \frac{1}{\sqrt{x}}\) est \(x\mapsto 2\sqrt{x}\), on a :
\(\forall k\ge 2, [2\sqrt{x}]_{k-1}^k\ge f(k)\), et : \(\forall k\ge 1, [2\sqrt{x}]_k^{k+1}\le f(k)\).
Donc :
\(\displaystyle \forall k\ge 2, 2(\sqrt{k}-\sqrt{k-1})\ge \frac{1}{\sqrt{k}}\),
et : \(\displaystyle \forall k\ge 1, 2(\sqrt{k+1}-\sqrt{k})\le \frac{1}{\sqrt{k}}\).
Ainsi, en sommant de \(\color{blue}{k=2}\) à \(n\), d’une part et de \(\color{green}{k=1}\) à \(n\), d’autre part, on a :
\(\displaystyle \forall n\ge 2, 2\sum_{k=2}^n(\sqrt{k}-\sqrt{k-1})\ge \sum_{\color{blue}{k=2}}^n\frac{1}{\sqrt{k}}\),
et : \(\displaystyle \forall n\ge 1, 2\sum_{k=1}^n(\sqrt{k+1}-\sqrt{k})\le \sum_{\color{green}{k=1}}^n\frac{1}{\sqrt{k}}\).
Donc, en arrangeant la première inégalité de sorte que la somme de droite commence à 1, on obtient :
\(\displaystyle \forall n\ge 2, 2\sum_{k=2}^n(\sqrt{k}-\sqrt{k-1}) \color{red}{+ 1}\ge \sum_{\color{red}{k=1}}^n\frac{1}{\sqrt{k}}\) ,
et : \(\displaystyle \forall n\ge 1, 2\sum_{k=1}^n(\sqrt{k+1}-\sqrt{k})\le \sum_{\color{green}{k=1}}^n\frac{1}{\sqrt{k}}\).
Soit en rassemblant les inégalités : \[\forall n\ge 2,2\sum_{k=2}^n(\sqrt{k}-\sqrt{k-1})+1\ge \sum_{k=1}^n\frac{1}{\sqrt{k}}\ge 2\sum_{k=1}^n(\sqrt{k+1}-\sqrt{k})\]
Les deux sommes qui encadrent \(\displaystyle \sum_{k=1}^n\frac{1}{\sqrt{k}}\) sont des sommes télescopiques, il vient donc :
\[\fbox{ \(\forall n\ge 2,2\sqrt{n}+1\ge \sum_{k=1}^n\frac{1}{\sqrt{k}}\ge 2(\sqrt{n+1}-1) \)}\]
L’encadrement de la somme d’intérêt étant fait, passons désormais à la détermination d’un équivalent au voisinage de \(+\infty\).
Détermination de l’équivalent
Comme \(n \ne 0\), on peut diviser l’encadrement ci-dessus par \(2\sqrt{n}\ge 0\), ce qui mène à :
\[ \forall n\ge 2,\frac{2\sqrt{n}+1}{2\sqrt{n}}\ge \frac{\displaystyle \sum_{k=1}^n\frac{1}{\sqrt{k}}}{2\sqrt{n}}\ge \frac{2(\sqrt{n+1}-1)}{2\sqrt{n}} \]
Soit :
\[ \forall n\ge 2,1+\frac{1}{2\sqrt{n}}\ge \frac{\displaystyle \sum_{k=1}^n\frac{1}{\sqrt{k}}}{2\sqrt{n}} \ge \sqrt{1+\frac{1}{n}}-\frac{1}{2\sqrt{n}} \]
Pour clore sur cette partie, étant donné que :
\(\displaystyle \underset{n \rightarrow +\infty}{\lim}(1+\frac{1}{ 2\sqrt{n}}) = 1\),
et : \(\displaystyle \underset{n \rightarrow +\infty}{\lim}(\sqrt{1+\frac{1}{n}}-\frac{1}{2\sqrt{n}})=1\),
on a, par le théorème d’encadrement : \[\underset{n \rightarrow +\infty}{\lim} \frac{\displaystyle \sum_{k=1}^n\frac{1}{\sqrt{k}}}{2\sqrt{n}} = 1\]
Soit :
\[\fbox{\(\sum_{k=1}^n \frac{1}{\sqrt{k}} \underset{n\rightarrow +\infty}{\sim}2\sqrt{n}\)}\]
Application : démonstration de la divergence de la série des \(\frac{1}{n}\)
Pour aller un peu plus vite, la fonction \(\displaystyle g : x\mapsto \frac{1}{x}\) vérifie les mêmes hypothèses que \(\displaystyle f : x\mapsto \frac{1}{\sqrt{x}}\) ; de plus, le graphe précédent et la comparaison graphique des aires restent sensiblement les mêmes. Ce qui nous permet d’obtenir l’encadrement suivant :
\[\int_{k-1}^k g(x)\text{d}x \ge g(k)\times 1 \ge \int_k^{k+1} g(x)\text{d}x\]
Soient les inégalités suivantes :
\(\displaystyle \forall k\ge 2, \int_{k-1}^k \frac{1}{x}\text{d}x\ge g(k)\), et : \(\displaystyle \forall k\ge 1, \int_k^{k+1} \frac{1}{x}\text{d}x\le g(k)\).
Donc, comme une primitive de \(\displaystyle x\mapsto \frac{1}{x}\) est \(x\mapsto \ln(x)\), on a :
\(\forall k\ge 2, [\ln(x)]_{k-1}^k\ge f(k)\), et : \(\forall k\ge 1, [\ln(x)]_k^{k+1}\le f(k)\).
Donc :
\(\displaystyle \forall k\ge 2, \ln(k)-\ln(k-1)\ge \frac{1}{k}\),
et : \(\displaystyle \forall k\ge 1, \ln(k+1)-\ln(k)\le \frac{1}{k}\).
Ainsi, en sommant de \(\color{blue}{k=2}\) à \(n\), d’une part et de \(\color{green}{k=1}\) à \(n\), d’autre part, on a :
\(\displaystyle \forall n\ge 2, 2\sum_{k=2}^n(\ln(k)-\ln(k-1))\ge \sum_{\color{blue}{k=2}}^n\frac{1}{k}\),
et : \(\displaystyle \forall n\ge 1, 2\sum_{k=1}^n(\ln(k+1)-\ln(k))\le \sum_{\color{green}{k=1}}^n\frac{1}{k}\).
Donc, en arrangeant la première inégalité de sorte que la somme de droite commence à 1, on obtient :
\(\displaystyle \forall n\ge 2, 2\sum_{k=2}^n(\ln(k)-\ln(k-1)) \color{red}{+ 1}\ge \sum_{\color{red}{k=1}}^n\frac{1}{k}\) ,
et : \(\displaystyle \forall n\ge 1, 2\sum_{k=1}^n(\ln(k+1)-\ln(k))\le \sum_{k=1}^n\frac{1}{k}\).
Soit en rassemblant les inégalités : \[\forall n\ge 2,2\sum_{k=2}^n(\ln(k)-\ln(k-1))+1\ge \sum_{k=1}^n\frac{1}{k}\ge 2\sum_{k=1}^n(\ln(k+1)-\ln(k))\]
Les deux sommes qui encadrent \(\displaystyle \sum_{k=1}^n\frac{1}{k}\) sont des sommes télescopiques, il vient donc :
\[\fbox{ \(\forall n\ge 2,\ln(n)+1\ge \sum_{k=1}^n\frac{1}{k}\ge \ln(n+1) \)}\]
L’encadrement de la somme d’intérêt étant fait, passons désormais à la détermination d’un équivalent au voisinage de \(+\infty\).
Détermination de l’équivalent
Comme \(n \ne 1\), on peut diviser l’encadrement ci-dessus par \(\ln(n)\), ce qui mène à :
\[\forall n\ge 2,\frac{\ln(n)+1}{\ln(n)}\ge \frac{\displaystyle \sum_{k=1}^n\frac{1}{k}}{\ln(n)}\ge \frac{\ln(n+1)}{\ln(n)} \]
Soit (démonstration ci-dessous) :
\[ \forall n\ge 2,1+\frac{1}{\ln(n)}\ge \frac{\displaystyle \sum_{k=1}^n\frac{1}{k}}{\ln(n)} \ge 1 + \frac{1 +\mathcal{o}(1)}{n\ln(n)}\]
Démonstration : \[\begin{align}\frac{\ln(n+1)}{\ln(n)} = \frac{\ln(n)+\ln(1+\frac{1}{n})}{\ln(n)} =1 + \frac{\ln(1+\frac{1}{n})}{\ln(n)} = 1+\frac{\frac{1}{n}+\underset{n\rightarrow +\infty}{\mathcal{o}(\frac{1}{n})}}{\ln(n)} = 1 + \frac{1 +\mathcal{o}(1)}{n\ln(n)}\end{align}\]
Pour clore, étant donné que :
\(\displaystyle \underset{n \rightarrow +\infty}{\lim}(1+\frac{1}{ \ln(n)}) = 1\), et : \(\displaystyle \underset{n \rightarrow +\infty}{\lim}( 1 + \frac{1 +\mathcal{o}(1)}{n\ln(n)})=1\),
On a, par le théorème d’encadrement : \[\underset{n \rightarrow +\infty}{\lim} \frac{\displaystyle \sum_{k=1}^n\frac{1}{k}}{\ln(n)} = 1\]
Soit :
\[\fbox{\(\sum_{k=1}^n \frac{1}{k} \underset{n\rightarrow +\infty}{\sim}\ln(n)\)}\]
Pour conclure sur cette partie :
Comme \(\displaystyle \underset{n \ge 1}{\sum}\ln(n)\)diverge grossièrement ( car : \(\displaystyle \underset{n\rightarrow + \infty}{\lim}\ln(n) = +\infty)\), il vient, d’après le théorème de comparaison des séries à termes positifs, la divergence de \(\displaystyle \underset{n \ge 1}{\sum}\frac{1}{n}.\)
Rappelons que l’utilisation du théorème de comparaison ci-dessus nécessite des termes généraux de signes constants (a fortiori positifs ici).
Nous venons ainsi de démontrer la nature de la très classique série harmonique \(\displaystyle \underset{n\ge 1}{\sum}\frac{1}{n}\).
Conclusion
Tu sais désormais comment appliquer rigoureusement la méthode de la comparaison série-intégrale, ainsi que les raisons d’existence des hypothèses nécessaires à son application, qui sont bien trop souvent mises sous le tapis. Pour t’entraîner à appliquer cette méthode, tu peux réaliser le début de ce sujet récent : Maths EML 2023 (mathématiques approfondies), ou traiter l’exercice 2 d’Ecricome ECS 2008 et celui de HEC ECS 2005.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !