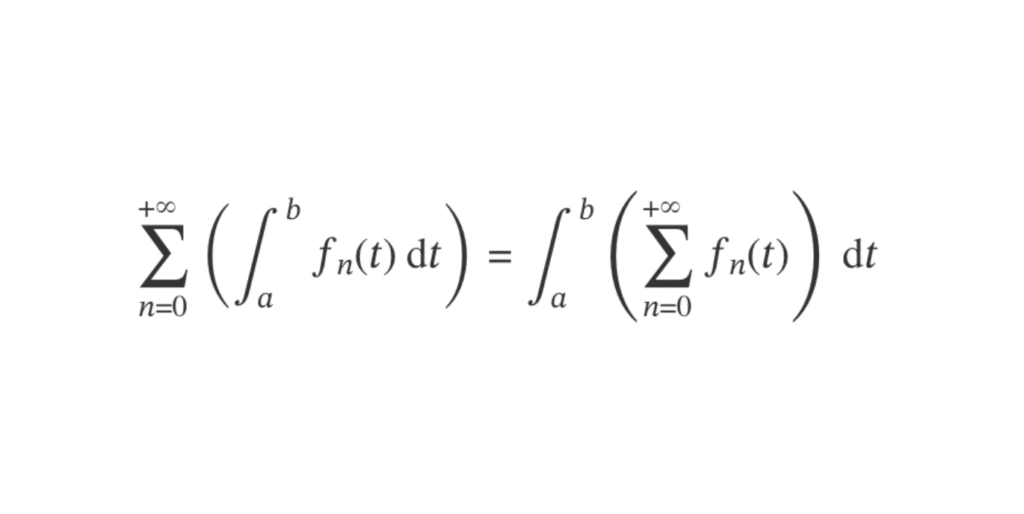Tu en as marre de ne pas comprendre pourquoi ton prof de prépa te crie dessus chaque fois que tu as l’audace d’affirmer que de toute façon, c’est instinctif, la série d’une intégrale, c’est logiquement l’intégrale de la série ? Tu aimerais percer tous les mystères qui entourent cette inversion ? Alors, cet article est fait pour toi ! Dans quelques minutes, tu sauras le pourquoi du comment et tu pourras surtout arrêter de faire l’erreur d’inverser ces signes sans réfléchir !
Permutation de \(\sum\) et \(\int\)
Enfin, nous y voilà ! Tu vas percer tous les secrets de cette inversion. Pour ce faire, on va considérer \(E\) l’ensemble des applications définies sur un intervalle \(I\) de \(\mathbb{R}\) non vide et non réduit à un point, et à valeurs dans \( \mathbb{R}\).
Soit \( \displaystyle\sum_{n\ge 0}{f_n} \) une série convergente (au moins simplement) d’applications continues par morceaux et intégrables sur \(I\).
1. On suppose la fonction \( x \mapsto \displaystyle\sum{f_n}(x)\) continue par morceaux sur \(I\) et que la série numérique \(\displaystyle \sum \int_I |f_n(t)|\,\mathrm{d}t \) converge.
Alors, la fonction \(x \mapsto \displaystyle\sum_{n\ge 0}{f_n}(x) \) est intégrable sur \(I\) et \(\displaystyle \int_I \sum_{n = 0}^{+\infty} {f_n} = \displaystyle \sum_{n = 0}^{+\infty} \int_I f_n\)
2. Si \(I = [a,b]\) avec \(a \le b\), si la convergence de la série \( \displaystyle\sum{f_n} \) est \(\color{red}{uniforme}\), et si les applications \((f_n)\) sont \(\color{red}{continues}\) sur \([a,b]\), alors la série \(\displaystyle \sum_{n \ge 0} \left(\int_a^b f_n(t)\,\mathrm{d}t\right)\) converge et
\[ \displaystyle \sum_{n = 0}^{+ \infty} \left(\int_a^b f_n(t)\,\mathrm{d}t\right) = \displaystyle
\int_a^b \left(\sum_{n = 0}^{+ \infty}f_n(t)\right) \,\mathrm{d}t
\]
Et voilà, tu sais tout ! Pas si instinctif finalement… N’hésite pas à aller consulter nos autres articles en cliquant ici !