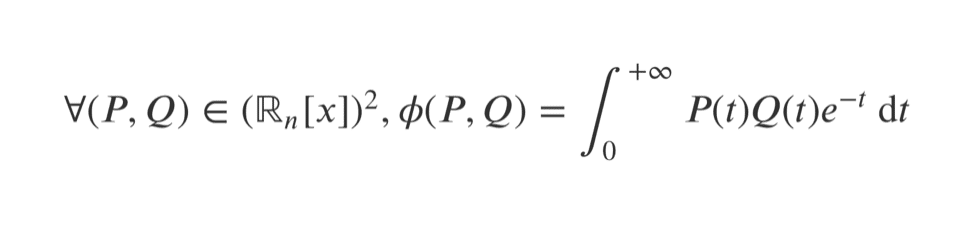Lorsque tu entames un sujet d’algèbre bilinéaire, l’une des premières questions, voire la première question, consiste souvent à démontrer qu’une application, souvent notée \(\langle. ,.\rangle\) est un produit scalaire. Cette question a beau faire partie des questions « faciles », elle est souvent bâclée par les étudiants, qui peuvent alors perdre jusqu’à la moitié des points pour la question.
Je te propose donc d’apprendre à démontrer rigoureusement qu’une application est un produit scalaire, en utilisant un exemple assez redondant : \(\forall (P,Q) \in (\mathbb{R}_n[x])^2, \langle P,Q\rangle= \displaystyle \int_{0}^{+
\infty} P(t)Q(t)e^{-t} \, \mathrm{d}t\)
Attention, cet article est uniquement destiné aux étudiants en maths approfondies.
Les éléments de rédaction que tu pourras imiter seront indiqués en gras.
Petit point notations
Dans les énoncés des sujets du concours, la question ressemble souvent à « montrer que \(\langle .,.\rangle\) est un produit scalaire ». Cependant, la notation \(\langle .,.\rangle\) sous-entend déjà que l’application est un produit scalaire.
Pour être plus rigoureux·se (ce qui peut être apprécié par les correcteurs), je te recommande de renommer l’application. On note provisoirement \(\phi\) l’application définie par \(\forall (P,Q) \in (\mathbb{R}_n[x])^2, \phi (P,Q)= \displaystyle \int_{0}^{+
\infty} P(t)Q(t)e^{-t} \, \mathrm{d}t\)
Tu pourras alors démontrer que \(\phi\) est bien un produit scalaire et conclure en écrivant \(\phi\) est bien un produit scalaire, que l’on note \(\langle .,. \rangle\).
Rappel de cours sur le produit scalaire
D’après ton cours, un produit scalaire est une forme, bilinéaire, symétrique, définie, positive. Si tu ne sais pas ce que l’une de ces notions signifie, je t’invite à te référer à ton cours.
Pour montrer qu’une application est un produit scalaire, on va donc démontrer ces cinq points. Toutefois, pour optimiser notre temps et en écrire le moins possible, nous n’allons pas utiliser le même ordre. On montrera que l’application est une forme, puis qu’elle est symétrique, puis bilinéaire, puis positive et enfin, définie.
La démonstration d’un produit scalaire
Montrer que \(\phi\) est une forme
Pour montrer que \(\phi\) est une forme, il nous suffit de montrer que \(\forall (P,Q) \in (\mathbb{R}_n[x])^2, \phi(P,Q) \in \mathbb{R}\).
Cette partie de la démonstration est parfois sautée par les étudiants, qui la considèrent évidente. C’est souvent loin d’être le cas. Il est impératif de montrer que les applications mises en jeu sont à valeurs dans \(\mathbb{R}\).
Cette partie de la démonstration est assez variable en fonction du produit scalaire. Pour notre exemple, tu l’auras peut-être compris, il s’agira de prouver la convergence de l’intégrale \(\displaystyle \int_{0}^{+
\infty} P(t)Q(t)e^{-t} \, \mathrm{d}t\), et ce, pour tout couple de polynômes \((P,Q)\).
Pour cela, plutôt qu’exprimer \(P\) et \(Q\) comme combinaison linéaire des \(x^k\), ce qui peut être très lourd en termes de notations, il sera beaucoup plus rapide et suffisant de prouver la convergence de l’intégrale \(\displaystyle \int_{0}^{+
\infty} t^ke^{-t} \, \mathrm{d}t\), et ce, pour tout \(k\) de \([\![0,n^2]\!]\).
Cela se démontre relativement facilement, par un critère de négligeabilité, en utilisant une intégrale de Riemann. Si tu souhaites un peu plus de détails sur cette méthode, clique sur ce lien.
Dès lors que tu as démontré cette convergence, tu peux utiliser la linéarité de l’intégration pour prouver que \(\displaystyle \int_{0}^{+
\infty} P(t)Q(t)e^{-t} \, \mathrm{d}t\) converge pour tout couple de polynômes \((P,Q)\). Ainsi, on a bien montré que \(\forall (P,Q) \in (\mathbb{R}_n[x])^2, \phi(P,Q) \in \mathbb{R}\). Cela signifie donc que \(\phi\) est une forme.
On a donc fini de démontrer le premier point.
Montrer que \(\phi\) est symétrique
Dans la plupart des cas, cette partie est la plus facile de la démonstration. Il y a bien sûr quelques exceptions, mais dans notre cas, la réponse est presque évidente. Il s’agit en effet de montrer que \(\forall (P,Q) \in (\mathbb{R}_n[x])^2, \phi(P,Q)=\phi(Q,P)\).
Plutôt que réécrire les intégrales, en disant que \(\forall (P,Q) \in (\mathbb{R}_n[x])^2, \displaystyle \int_{0}^{+
\infty} P(t)Q(t)e^{-t} \, \mathrm{d}t=\displaystyle \int_{0}^{+
\infty} Q(t)P(t)e^{-t} \, \mathrm{d}t\), ce qui est long et inutile, tu peux le rédiger ainsi : \(\phi\) est symétrique, par commutativité du produit dans \(\mathbb{R}\).
Cette phrase suffit à aboutir la démonstration de ce point.
Montrer que \(\phi\) est bilinéaire
Normalement, ce point se démontrerait en deux points : la linéarité à gauche, puis la linéarité à droite. Toutefois, puisque l’on a démontré juste avant que \(\phi\) était symétrique, il est suffisant de seulement démontrer la linéarité à gauche. Cela signifie que l’on cherche à démontrer que \(\forall (P_1,P_2,Q) \in (\mathbb{R}_n[x])^3, \forall \lambda \in \mathbb{R}, \phi(\lambda P_1+P_2,Q)=\lambda \phi(P_1,Q) +\phi(P_2,Q) \).
Je ne détaille pas ce point, il suffit pour cela d’utiliser la linéarité de l’intégration.
Ainsi, d’après les points 2 et 3, \(\phi\) est bilinéaire symétrique.
Montrer que \(\phi\) est positive
Démontrer ce point consiste à prouver que \(\forall P \in (\mathbb{R}_n[x]), \phi(P,P) \ge0 \). Encore une fois, ce point est relativement facile : il suffit d’utiliser la croissance de l’intégration.
Soit \(P \in \mathbb{R}_n[x]\). On a \(\phi(P,P)=\displaystyle \int_{0}^{+
\infty} P(t)^2e^{-t} \, \mathrm{d}t\).
Or, \(\forall t \in \mathbb{R}^+, P(t)^2e^{-t} \ge 0\).
Ainsi, par croissance de l’intégration, les bornes étant rangées dans l’ordre croissant, on a \(\displaystyle \int_{0}^{+
\infty} P(t)^2e^{-t} \, \mathrm{d}t \ge 0\), soit \(\phi(P,P) \ge 0\).
Donc, \(\phi\) est positive.
Montrer que \(\phi\) est définie
Prouver que \(\phi\) est définie, c’est prouver \(\forall P \in (\mathbb{R}_n[x]), \phi(P,P)=0 \Rightarrow P=0\). Ce point se montre en utilisant un théorème d’analyse.
Soit \(P \in \mathbb{R}_n[x]\) tel que \(\phi(P,P)=0\), on a donc \(\displaystyle \int_{0}^{+
\infty} P(t)^2e^{-t} \, \mathrm{d}t=0\).
Dans la mesure où l’intégrande est positive et l’intégrale est nulle, le cours assure que \(\forall t \in \mathbb{R}^+, P(t)^2e^{-t}=0\). Et comme \(\forall t \in \mathbb{R}^+, e^{-t} \ne0\), on a donc \(\forall t \in \mathbb{R}^+, P(t)^2=0\), soit encore \(\forall t \in \mathbb{R}^+, P(t)=0\), et donc \(P=0\).
Ainsi, on a bien \(\forall P \in (\mathbb{R}_n[x]), \phi(P,P)=0 \Rightarrow P=0\) : \(\phi\) est définie.
Conclusion
On a donc montré que \(\phi\) est une forme bilinéaire symétrique définie positive : c’est un produit scalaire. On le notera donc \(\langle .,.\rangle\).
Voilà, tu sais désormais démontrer qu’une application est un produit scalaire !