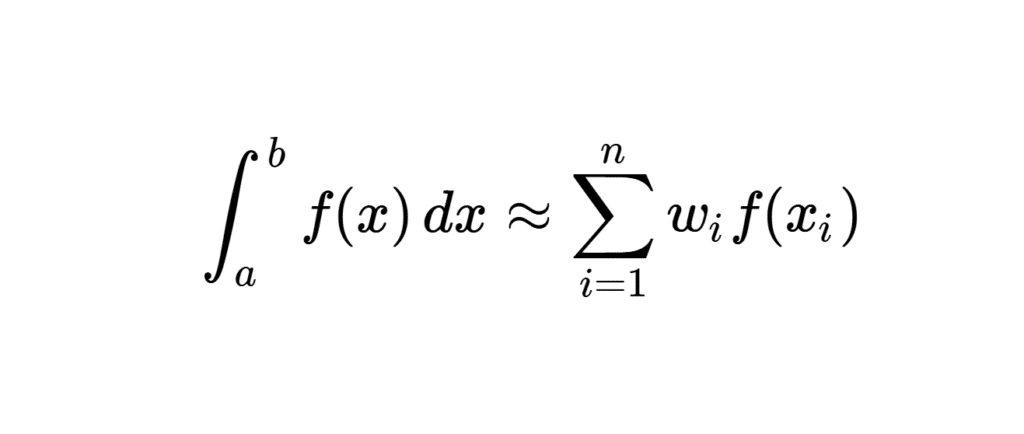La méthode de quadrature de Gauss est une méthode hors programme permettant de calculer de manière précise une valeur approchée d’une intégrale. Cette méthode se fonde sur de nombreuses notions présentes au programme, ou en lien direct avec ce dernier : intégrales, séries, formules de Taylor, polynômes de Legendre ou encore produits scalaires.
Introduction
La quadrature de Gauss est une méthode d’intégration utilisée pour calculer approximativement l’intégrale d’une fonction sur un intervalle donné. Cette méthode est particulièrement efficace, car elle permet d’obtenir une estimation précise de l’intégrale en utilisant un nombre relativement faible de points d’évaluation (la définition de ces points sera donnée par la suite). Ces points sont choisis de manière optimale pour maximiser la précision de l’approximation.
La méthode de quadrature de Gauss repose sur l’utilisation de polynômes orthogonaux (d’où le lien avec l’algèbre bilinéaire), plus précisément les polynômes de Legendre, pour déterminer les points d’évaluation et les poids associés.
Voici les premiers polynômes de Legendre qui pourront être utiles :
\(
\begin{aligned}
L_0(x) & = 1 \\
L_1(x) & = x \\
L_2(x) & = \frac{1}{2}(3x^2 – 1) \\
L_3(x) & = \frac{1}{2}(5x^3 – 3x) \\
L_4(x) & = \frac{1}{8}(35x^4 – 30x^2 + 3) \\
L_5(x) & = \frac{1}{8}(63x^5 – 70x^3 + 15x)
\end{aligned}
\)
Notons toutefois que les démonstrations des éléments que nous verrons dans cet article ne seront pas données. Elles sont toutefois présentes dans ce très bon article de J. F. Cossuta avec sa correction.
Problème d’intégration
Soit \( f(x) \) une fonction continue définie sur un intervalle \( [a, b] \). L’objectif est de calculer l’intégrale de \( f(x) \) sur cet intervalle : \(I = \int_a^b f(x) \, dx\)
Sauf que, parfois, il est impossible ou très complexe de primitiver la fonction intégrée, de sorte que l’on cherche à approximer cette valeur de l’intégrale en passant par une autre méthode. C’est le cas de la méthode des rectangles, que tu connais sûrement déjà. Ici, la méthode de quadrature de Gauss (ou méthode de quadrature de Gauss-Legendre) est plus précise, mais plus technique à mettre en application !
La méthode de quadrature de Gauss consiste à approximer cette intégrale par une somme de valeurs de la fonction \( f(x) \) évaluées en des points spécifiques, appelés points de Gauss, avec des poids correspondants (dits poids de Gauss). L’approximation est donnée par :
\[\int_a^b f(x) \, dx \approx \sum_{i=1}^{n} w_i f(x_i)\] où \( x_i \) sont les points de Gauss et \( w_i \) les poids associés.
Formulation de la méthode de Gauss
Points de Gauss
Les points de Gauss \( x_i \) sont les racines des polynômes de Legendre \( P_n(x) \), qui sont des polynômes orthogonaux sur l’intervalle \( [-1, 1] \). Ces points sont choisis pour minimiser l’erreur de quadrature.
Ces points \( x_1, x_2, \dots, x_n \) sont symétriques par rapport à l’axe central \( x = 0 \) sur l’intervalle \( [-1, 1] \). Cela signifie que si tu travailles avec \(n=2\) et que tu as déjà trouvé une racine de \(L_2\), tu en déduis directement la deuxième qui est son opposé.
Poids de Gauss
Les poids \( w_i \) sont liés aux dérivées de \( P_n(x) \) et sont donnés par la formule suivante :
\[w_i = \frac{2}{(1 – x_i^2) \left( P_n'(x_i) \right)^2}\]
Propriétés de la quadrature de Gauss
La quadrature de Gauss présente plusieurs propriétés importantes qui la rendent très efficace pour les approximations d’intégrales.
Exactitude pour les polynomiaux
L’une des propriétés les plus remarquables de la méthode de Gauss est qu’elle donne une estimation exacte de l’intégrale pour les polynômes de degré \( 2n – 1 \) ou moins. C’est-à-dire que si \( f(x) \) est un polynôme de degré \( 2n – 1 \), alors la quadrature de Gauss donne \( I = \int_a^b f(x) \, dx \) exactement.
Toutefois, l’intérêt de cette propriété est restreint dans le cadre du programme de maths appliquées comme approfondies, puisque l’on pourrait directement déterminer une primitive du polynôme en question.
Symétrie des points et poids
Les points \( x_i \) sont symétriques par rapport à \( x = 0 \) (l’axe central) sur l’intervalle \( [-1, 1] \). Cette symétrie permet une réduction significative des erreurs dans l’approximation de l’intégrale.
De plus, les poids \( w_i \) sont calculés de manière à garantir que la somme pondérée des évaluations de \( f(x) \) est optimale pour l’approximation de l’intégrale. En fait, l’idée globale des poids est d’affecter plus ou moins d’importance aux \(f(x_i)\) en fonction des \(x_i\).
Erreur de la quadrature de Gauss
L’erreur \( E_n \) associée à une quadrature de Gauss est généralement de l’ordre de \( O\left(\frac{1}{(2n)!}\right) \) lorsque la fonction à intégrer est suffisamment lisse. Cette erreur diminue très rapidement avec l’augmentation de \( n \), ce qui rend la méthode de Gauss très efficace pour des intégrales nécessitant une grande précision.
À l’aide d’une démonstration faisant intervenir l’inégalité de Taylor-Lagrange, on peut en effet obtenir :
\[
\left| \int_a^b f(x) \, dx – \sum_{k=1}^n a_k f(x_k) \right|
\leq \frac{M\| P_n \|^2}{(2n)!}.
\]
où \(M_n = \sup_{t \in [a,b]} \left| f^{(n)}(t) \right|\) et la famille \((P_r)_{r \in \mathbb{}N}\) est une famille de polynômes unitaires deux à deux orthogonaux où \(P_0 = 1\).
Cela signifie directement qu’il est possible de majorer la différence entre l’intégrale que l’on cherche à calculer et notre approximation par un élément dont la vitesse de convergence est de l’ordre de \(\frac{1}{(2n)!}\), c’est-à-dire rapide pour des \(n\) de plus en plus grands !
Exemple
Considérons l’intégrale suivante :
\[I = \int_{-1}^1 e^{-x^2} \, dx\]
On cherche rapidement une primitive et on se rend compte qu’on va avoir bien du mal à en trouver une… En utilisant la quadrature de Gauss-Legendre avec \( n = 2 \), nous trouvons néanmoins une approximation de cette intégrale.
\[\text{Soit} \quad n = 2, \quad x_1 = -\frac{\sqrt{3}}{3}, \quad x_2 = \frac{\sqrt{3}}{3}\] (trouvé en calculant les racines du polynôme de Legendre pour \(n=2\), c’est-à-dire \(L_2(x) = \frac{1}{2}(3x^2 – 1) \))
Les poids sont \( w_1 = w_2 = 1 \) (en utilisant la formule pour les déterminer en fonction des \(x_i\) trouvés juste au-dessus).
L’approximation de l’intégrale est donc :
\[
\begin{aligned}
I & \approx \sum_{i=1}^{2} w_i f(x_i) = f\left(-\frac{\sqrt{3}}{3}\right) + f\left(\frac{\sqrt{3}}{3}\right) \\I & \approx e^{-\left(\frac{\sqrt{3}}{3}\right)^2} + e^{-\left(\frac{\sqrt{3}}{3}\right)^2} \\I & \approx 2 e^{-\frac{1}{3}}
\end{aligned}
\]
Cela donne une approximation de l’intégrale de \( I \approx 1.954 \) tout en sachant que le résultat exact vaut environ \(1.4936482656\). On a donc une approximation très correcte, puisque l’on travaille avec un \(n\) très petit.
Et pour \(n= 6\) , on obtient l’approximation \(\int_{-1}^1 e^{-x^2} \, dx \approx 1.4936260192\).
Cet exemple souligne précisément la vitesse de convergence de l’approximation pour des \(n\) de plus en plus grands. Ici, passer de \(2\) à \(6\) permet de passer à une approximation de l’ordre de \(10^-5\) près !
Conclusion
En définitive, la méthode de quadrature de Gauss (ou Gauss-Legendre) est une méthode d’approximation intégrale (au même titre que la méthode des rectangles) qui a le mérite d’être très précise, mais dont la contrepartie est une démonstration plus longue que pour la méthode des rectangles.
Cette méthode peut largement faire l’objet d’un sujet de Maths I, car elle permet d’aborder un grand nombre de chapitres au programme. Il n’y a désormais plus qu’à espérer que cette notion tombe le jour J aux concours !
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !