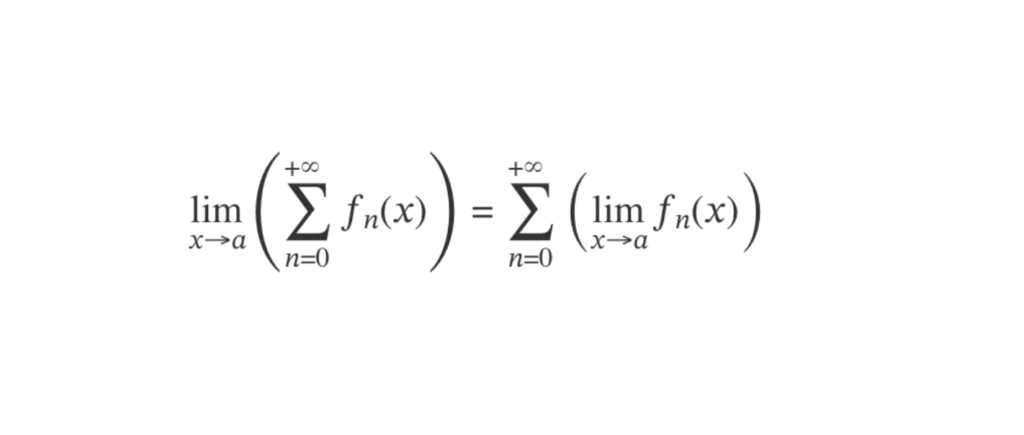Dans cet article, je te détaille la méthode et les prérequis nécessaires pour affirmer que, dans certains cas, la limite d’une série est égale à la série de la limite ! Cette notion est bien évidemment hors programme, mais je te conseille fortement de te familiariser avec avant tes écrits ou tes oraux.
Attention, cette notion est hors programme dans le cas des sommes avec le symbole infini. En effet, lorsqu’une somme est finie, le passage à la limite classique est « légal ». En revanche, dès que l’on met en jeu une série infinie, ce passage à la limite classique n’est plus « légal », car il est seulement réalisable sous certaines conditions, d’où cet article…
Convergence simple et convergence uniforme de suites de fonctions
On note \(E\) l’ensemble des applications définies sur un intervalle \(I\) de \(\mathbb{R}\) non vide et non réduit à un point, et à valeurs dans \( \mathbb{R}\).
Soit \((f_n)_{n \in\mathbb{N}}\) une suite d’éléments de \(E\) et \(f\) un élément de \(E\). On note \(\|f\|_{\infty} = sup |f|\) sur \(I\).
On dit que la suite \((f_n)_{n \in\mathbb{N}}\) converge \(\color{red}{simplement}\) vers \(f\) sur \(I\) si et seulement si :
\[\forall x \in I, \lim \limits_{n \to +\infty} (f_n)_{n \in\mathbb{N}}\ (x) = f(x)\]
On dit que la suite \((f_n)_{n \in\mathbb{N}}\) converge \(\color{red}{uniformément}\) vers \(f\) sur \(I\) si et seulement si :
à partir d’un certain rang, \[\lim \limits_{n \to +\infty} \|f_n \ – f\|_{\infty} = 0\]
Remarque : la convergence uniforme implique la convergence simple, alors que la réciproque est fausse.
Les trois types de convergence des séries de fonctions
On notera \(E\) l’ensemble des applications définies sur un intervalle \(I\) de \(\mathbb{R}\) non vide et non réduit à un point, et à valeurs dans \( \mathbb{R}\).
Soit \((f_n)_{n \in\mathbb{N}}\) une suite d’éléments de \(E\). On pose \(\forall n \in \mathbb{N}, S_n = \displaystyle \sum_{k=0}^{n}f_k\).
On appelle série de fonctions \(\displaystyle\sum{f_n}\) la suite de fonction \((S_n)_{n \in\mathbb{N}}\).
- On dit que \(\displaystyle\sum{f_n}\) converge \(\color{red}{simplement}\) si et seulement si la suite \((S_n)_{n \in\mathbb{N}}\) converge simplement.
- On dit que \(\displaystyle\sum{f_n}\) converge \(\color{red}{uniformément}\) si et seulement si la suite \((S_n)_{n \in\mathbb{N}}\) converge uniformément.
- Si toutes les fonctions de la suite \((f_n)_{n \in\mathbb{N}}\) sont bornées, on dit que \(\displaystyle\sum{f_n}\) converge \(\color{red}{normalement}\) si et seulement si la série \(\sum|f_n|_{\infty}\) converge.
Remarque : la convergence normale implique la convergence simple.
Permutation de la somme et de la limite
On suppose que la série d’applications \(\left( \displaystyle\sum_{n\ge 0}{f_n} \right)\) converge uniformément sur \(I\) et que pour un \(a \in I\), toutes les applications \(f_n\) ont une limite en \(a\) (dépendant de \(n)\).
Alors, la série \(\displaystyle\sum_{n\ge 0}{\left( \displaystyle \lim \limits_{x \to a} f_n(x)\right)}\) converge, la fonction \( x \mapsto \displaystyle\sum_{n\ge 0}{f_n(x)} \) a une limite lorsque \(x \to a\) et \(\lim \limits_{x \to a}\left( \displaystyle\sum_{n = 0}^{+ \infty} f_n(x) \right) = \displaystyle\sum_{n = 0}^{+ \infty} \left( \displaystyle \lim \limits_{x \to a} f_n(x)\right)\)
Ces définitions semblent compliquées à appliquer au premier abord. C’est pourquoi je te propose un exercice pour t’entraîner. Je te conseille de chercher par toi-même avant de regarder la correction, cela te sera plus utile !
Exercice
Énoncé
Pour \(x \ge 0\) et \(n \ge 1\), on pose \(f_n(x) = \displaystyle \frac{n}{1 + n(1 + x)}\)
1. Démontrer que la suite de fonctions \((f_n)_{n \ge 1}\) converge simplement sur \([0,+\infty[\) vers la fonction \(f\) que l’on précisera.
2. Démontrer que la convergence est en réalité uniforme sur \([0,+\infty[\).
Corrigé
1. L’étude de la convergence simple revient à étudier la convergence des suites \((f_n(x))_{n \ge 1}\) lorsque \(x \ge 0\) est fixé. Mais \(x\) étant fixé, puisque \(1 + x > 0\), on a clairement \(f_n(x)\) qui tend vers \( \displaystyle\frac{1}{1 + x}\). Donc, la suite de fonctions \((f_n)\) tend simplement sur \([0,+\infty[\) vers la fonction \(f\) définie par \(f(x) = \displaystyle \frac{1}{1 + x}\).
2. On calcule \(f_n(x) – f(x)\), puis on majore \(|f_n(x) – f(x)|\). On a donc \(f_n(x) – f(x) = \displaystyle \frac{-1}{(1 + x) + n(1 + x)^2}\).
Or, pour \(x \ge 0\), on a \((1 + x) + n(1 + x)^2 \ge n(1 + x)^2 \ge n\) et donc \(|f_n(x) – f(x)| =\displaystyle \frac{1}{(1 + x) + n(1 + x)^2} \le \displaystyle \frac{1}{n}\).
Cette dernière quantité ne dépend plus de \(x \in [0,+\infty[\) et tend vers 0. Donc \((f_n)\) converge uniformément vers \(f\) sur \([0,+\infty[\).
C’est tout pour cet article ! N’hésite pas à aller en consulter d’autres en cliquant sur ce lien !