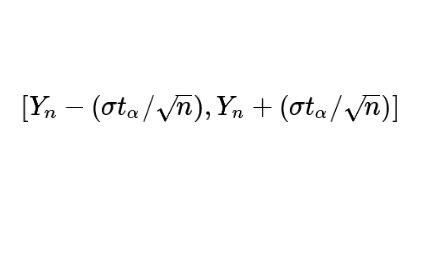Dans cet article, je vais te montrer les différentes méthodes et étapes pour construire un intervalle de confiance. Beaucoup d’élèves négligent cette partie du programme, sans doute car elle leur semble complexe, mais aussi car les questions des sujets de Parisiennes sur cette notion sont souvent situées vers la fin de la dernière partie. C’est dommage car, en réalité, la construction d’un intervalle de confiance est assez simple, elle nécessite surtout d’apprendre les différentes étapes et de les rédiger presque mécaniquement sur sa copie, en adaptant avec les données de l’énoncé. Si tu veux te distinguer des autres élèves aux concours, lis attentivement cet article.
N’hésite pas à revoir tes cours sur les convergences et les estimations avant, car les intervalles de confiance utilisent des théorèmes et des propriétés de ces chapitres. Pour cela, tu peux aller relire nos cours de probabilités.
Utilité des intervalles de confiance
Les intervalles de confiance servent à estimer la valeur d’un paramètre inconnu \(\theta\), avec une probabilité minimale fixée à l’avance. Pour cela, on sera fréquemment amené plutôt à estimer la valeur de g(\(\theta\)) (où g est une fonction quelconque de \(\theta\)).
Dans la vie de tous les jours, cette méthode est souvent utilisée lors des sondages politiques, afin d’estimer jusqu’à quel point le résultat de l’élection obtenu est conforme à la réalité, par exemple.
Définition d’un intervalle de confiance
Soient \((X_1,X_2,…,X_n)\) un échantillon de variables indépendantes et identiquement distribuées, \(U_n\) et \(V_n\) deux estimateurs de \(\theta\).
On suppose que : \(P(U_n<V_n)=1\).
Soit \(\alpha\) appartenant à \(]0,1[\). On dit que \([U_n,V_n]\) est un intervalle de confiance pour \(g(\theta)\) au niveau de confiance \(1-\alpha\) (ou de risque \(\alpha\)).
Méthodes
Méthode 1 : utilisation de l’inégalité de Bienaymé-Tchebychev pour l’estimation par intervalle d’un paramètre en six étapes
Soit \(X\) une variable dont la loi a pour paramètre \(p\) inconnu. Soient \((X_1,X_2,…,X_n)\) une suite de variables indépendantes et identiquement distribuées de même loi que \(X\) dont le paramètre \(p\) est inconnu.
On note \(Y_n = (X_1,X_2,…,X_n)/n\), la moyenne empirique.
Étape 1 : vérifier que \(Y_n\) est bien un estimateur de \(\theta\), sans biais et convergent
- \(Y_n\) est un estimateur de \(\theta=p\), car c’est une fonction de \(n\) variables indépendantes et identiquement distribuées ne dépendant pas du paramètre \(p\)
- \(Y_n\) est sans biais, car \(E(Y_n)=p\)
- \(Y_n\) est convergent, car \(Y_n\overset{\mathbb{P}}
{\rightarrow} p\)
Étape 2 : utiliser l’inégalité de Bienaymé-Tchebychev
Après avoir vérifié les hypothèses du théorème, on peut appliquer la formule : \(\forall \epsilon>0\),
\(P(\ |Y_n-p|>\epsilon)\le V(Y_n)/\epsilon^2\)
Étape 3 : multiplier l’inégalité par \(-1\) et ajouter \(1\) (penser à changer le sens de l’inégalité)
\(1-P(\ |Y_n-p|>\epsilon)\ge 1-V(X)/(n\epsilon^2)\) car \(V(Y_n)=V(X)/n\)
Étape 4 : isoler \(\theta\)
\(P(Y_n-\epsilon \le p\le Y_n+\epsilon)\ge 1-V(X)/(n\epsilon^2)\)
Étape 5 : majorer la variance et chercher la valeur de \(\epsilon\)
Afin d’être sûr que les « estimateurs » trouvés ne dépendent pas du paramètre inconnu (car oui, je te le rappelle, un estimateur ne dépend JAMAIS du paramètre), on est souvent amené à majorer la variance.
- On suppose que \(V(X)\) est majorée par M. On a alors : \(P(Y_n-\epsilon\le p \le Y_n+\epsilon)\ge 1-(M/(n\epsilon^2))\)
- Par exemple, si on considère que \(X\) suit une loi de Bernoulli de paramètre \(p\), comme : \(p(1-p) \le 1/4\), on réécrit l’inégalité comme telle : \(P(Y_n-\epsilon\le p \le Y_n+\epsilon)\ge 1-(1/(4n\epsilon^2))\)
- On choisit \(\epsilon\) tel que : \(M/(n\epsilon^2)= \alpha \Leftrightarrow \epsilon = (\sqrt{M/(n\alpha)})\)
Étape 6 : conclure avec l’intervalle de confiance trouvé, qui est de la forme \([Y_n-\epsilon , Y_n+\epsilon]\)
Ainsi : \([Y_n- (\sqrt{M/(n\alpha)}), Y_n+(\sqrt{M /(n\alpha)})]\) est un intervalle de confiance pour \(p\) au niveau de confiance \(1-\alpha\)
Méthode 2 : utilisation des propriétés du théorème central limite pour l’estimation par intervalle du paramètre d’une loi normale en six étapes
Soient \((X_1,X_2,…,X_n)\) une suite de variables indépendantes et identiquement distribuées suivant une loi normale d’écart-type \(\sigma\) inconnu et d’espérance \(\mu\). Soit \(Y_n = (X_1+X_2+…,X_n)/n\), la moyenne empirique.
Étape 1 : écrire ce que l’on souhaite obtenir
On veut avoir : \(P(|Y_n-\mu|\le \epsilon)\ge 1-\alpha\)où \(Y_n \hookrightarrow
\mathcal{N}(\mu,\sigma^2/n)\)(par stabilité, les \(X_i\) sont indépendants).
Étape 2 : utiliser le théorème central limite pour se ramener à une loi normale centrée réduite
Après avoir vérifié les hypothèses du théorème :
\((Y_n-\mu)(\sqrt{n}/\sigma) \hookrightarrow
\mathcal{N}(0,1)\)
Étape 3 : utiliser les propriétés de la fonction de répartition de la loi normale centrée réduite
On note \(\Phi\) la fonction de répartition de la loi normale centrée réduite.
\(P(|(Y_n-\mu)(\sqrt{n}/\sigma)|\le \epsilon\sqrt{n}/\sigma)\ge 1-\alpha\)
=\(\Phi(\epsilon\sqrt{n}/\sigma)-\Phi(-\epsilon\sqrt{n}/\sigma)\)
= \(2\Phi (\epsilon\sqrt{n}/\sigma)-1\)
Étape 4 : chercher \(\epsilon\) et \(t_\alpha\)
- On cherche \(\epsilon\) tel que : \(2\Phi (\epsilon\sqrt{n}/\sigma)-1 \ge 1-\alpha \Leftrightarrow \Phi (\epsilon\sqrt{n}/\sigma)\ge 1-(\alpha/2)\)
\(\Phi\) est une fonction strictement croissante, continue de \(\mathbb{R}\) dans \(]0,1[\), donc bijective.
D’après le théorème de la bijection monotone, on peut trouver \(t_\alpha\) tel que : \(\Phi(t_\alpha) = 1-(\alpha/2)\).
- On cherche maintenant \(\epsilon\) tel que : \(\epsilon\sqrt{n}/\sigma=t_\alpha\) \(\Leftrightarrow \epsilon =( t_\alpha\sigma)/\sqrt{n}\)
Étape 5 : encadrer \(\mu\)
\(P(Y_n-(\sigma t_\alpha/\sqrt{n})\le\mu\le Y_n+(\sigma t_\alpha/\sqrt{n}))= 1-\alpha\)
Étape 6 : conclure
Ainsi, l’intervalle de confiance recherché est : \([Y_n-(\sigma t_\alpha/\sqrt{n}), Y_n+(\sigma t_\alpha/\sqrt{n})]\)
Méthode 3 : utilisation de la méthode de Monte-Carlo pour estimer un paramètre de Bernoulli
Avant le changement de programme, lorsqu’une variable aléatoire suivait une loi de Bernoulli, on devait construire de A à Z l’intervalle de confiance en utilisant les étapes de la méthode 1. Maintenant, avec le nouveau programme, on peut directement donner l’intervalle de confiance de son paramètre en utilisant le cours, sans avoir à tout démontrer.
Énoncé du cours
Soit \(n\in\mathbb{N}\). Soit \(X \hookrightarrow\mathcal{B}(p)\). On pose \((X_{i})_{1 \le i \le n}\) des variables indépendantes et identiquement distribuées de même loi que \(X\). Soit \(Y_n\) la moyenne empirique des \(X_i\).
Alors : \([Y_n- (1/2\sqrt{n\alpha}), Y_n+(1/2\sqrt{n\alpha})]\) est un intervalle de confiance pour \(p\) au niveau de confiance \(1-\alpha\).
Remarques
Remarque 1 : valeurs à connaître
Même si le programme ne l’exige pas explicitement, il est utile de connaître certaines valeurs de \(\alpha\) :
- \(\Phi (1,96) \approx 0,975\), correspond à \(\alpha=0,05\)
- \(\Phi (2,58) \approx 0,995\), correspond à \(\alpha = 0,01\)
Remarque 2 : construction d’un intervalle de confiance asymptotique
Un cas particulier des intervalles de confiance est l’intervalle de confiance asymptotique. Sa construction nécessite à peu près les mêmes étapes que la deuxième méthode ci-dessus pour construire un intervalle de confiance non asymptotique.
Définition de l’intervalle de confiance asymptotique
Soient \((X_1,X_2,…,X_n)\), des variables indépendantes et identiquement distribuées, \(U_n\) et \(V_n\), deux estimateurs de \(\theta\).
On suppose que : \(P(U_n\le V_n) = 1\). On dit que \([U_n,V_n]\) est un intervalle de confiance asymptotique pour \(g(\theta)\), au risque \(\alpha\) s’il existe \((\alpha_n)_{n \in \mathbb{N*}}\) (des réels de \([0,1]\)) vérifiant :
- \(P(U_n\le g(\theta)\le V_n)\ge 1-\alpha_n\)
- \(\lim \limits_{n \to +\infty}(\alpha_n)=\alpha\)
Conclusion
L’article touche à sa fin, j’espère qu’il t’aura permis de mieux comprendre les intervalles de confiance et que tu feras la différence aux concours en t’attaquant à ces questions que les autres candidats n’oseront pas essayer.
N’hésite pas à consulter nos autres ressources !