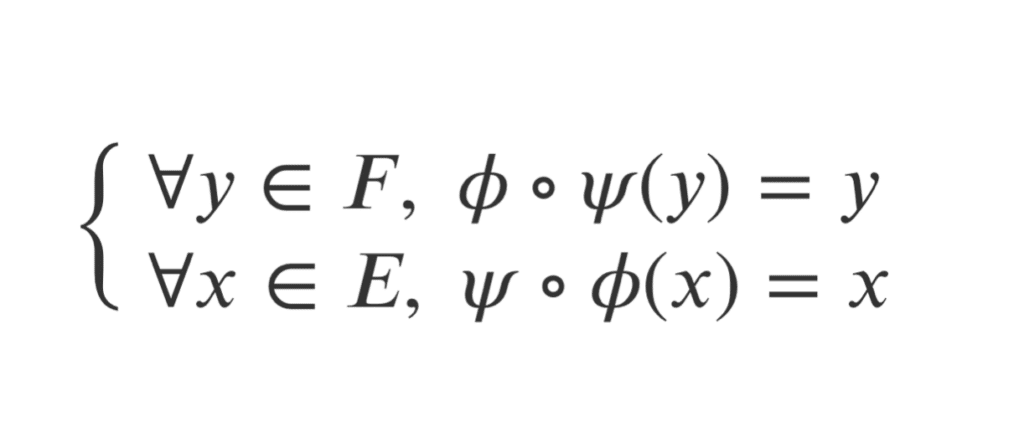Une des questions les plus fréquentes aux concours (en maths appliquées et approfondies) est de démontrer qu’une application \( \phi \) d’un espace \(E\) vers un espace \(F\) est un isomorphisme. Dans cet article, on te récapitule les différentes méthodes pour y arriver !
Avant de commencer, il est nécessaire de s’assurer que l’application en question est bien une application linéaire ! Si l’énoncé ne le précise pas, tu dois impérativement faire la démonstration sur ta copie avant de commencer à démontrer que tu es en présence (ou non) d’un isomorphisme.
On rappelle qu’un isomorphisme de \(E\) sur \(F\) est une application linéaire bijective de \(E\) sur \(F\).
Si tu as prouvé que l’application en question était bien une application linéaire (ou que l’énoncé l’indique), tu peux alors passer à l’étape suivante, qui fait l’objet de cet article. Deux cas de figure principaux se présentent alors.
Cas numéro 1 : si au moins un des deux espaces est de dimension infinie ou qu’il n’y a pas d’informations précises sur les dimensions
Plusieurs méthodes s’offrent à toi.
Méthode 1
Cette méthode revient à utiliser la première définition de la bijectivité. Il s’agit de montrer que tout élément de l’espace d’arrivée admet un unique antécédent dans l’espace de départ. Autrement dit, on veut montrer que :
\(
\forall y \in F ,\
\exists! x \in E \ \text {tel que}\ \phi(x)=y
\)
Méthode 2
Cette méthode se rattache à la méthode décrite ci-dessus, sauf qu’on va jouer sur la définition de la bijectivité.
Pour montrer qu’une application est bijective, tu peux en effet montrer qu’elle est injective puis surjective en revenant aux définitions de base de l’injection et de la surjection.
Méthode 3
Cette méthode est un peu plus délicate. Elle consiste à identifier une application \( \psi \) de \(F\) dans \(E\) vérifiant les conditions suivantes :
\(
\begin{cases}
\forall y \in F ,\ \phi \circ \psi(y) = y \\
\forall x \in E ,\ \psi\circ \phi(x) = x \\
\end{cases}
\)
Remarque : dans le cas où \(E = F\), \( \psi \) correspond tout simplement à \( \phi ^{-1}\)
Méthode 4
Cette méthode implique de revenir à la définition.
En effet, \( \phi \) est un isomorphisme si et seulement si \( \text{Ker} \ \phi= {{0_E}} \) et que \( \text{Im} \ \phi = F \)
C’est donc ce que tu devras essayer de montrer !
Cas numéro 2 : si on sait que \(E\) et \(F\) sont des SEV de dimension finie
Ce cas est largement préféré par les candidats. En plus des méthodes décrites ci-dessus, de nouveaux outils puissants peuvent être utilisés, en raison de la dimension finie des espaces vectoriels considérés.
Méthode 1
Cette méthode implique de travailler sur les bases de \(E\) et de \(F\).
En effet, si tu arrives à prouver que \( \phi \) transforme une base de \(E\) en une base de \(F\), alors tu pourras en conclure que \( \phi \) est un isomorphisme !
Autrement dit, si \((e_1,…,e_n)\) est une base de \(E\) et que \((\phi(e_1),…,\phi(e_n))\) est une base de \(F\), alors \( \phi \) est un isomorphisme !
Méthode 2
Cette méthode met en jeu la représentation matricielle de l’application \( \phi \).
Si la matrice représentative de \( \phi \) est inversible, alors tu peux conclure que \( \phi \) est une bijection.
Méthode 3
ATTENTION ! Cette méthode ne peut s’appliquer que si l’on sait déjà que \(\text{dim}(E) = \text{dim}(F)\)
Si tu arrives à montrer que \( \phi \) est injective OU surjective, alors la dimension finie des espaces vectoriels te permet directement d’affirmer que \( \phi \) est bijective, donc que l’application sur laquelle tu travailles est un isomorphisme.
Conclusion
Tu sais maintenant comment montrer qu’une application est un isomorphisme !
Quelques précisions en plus :
– dans le cas où \(E\) et \(F\) sont des SEV de dimension finie, montrer que \( \phi \) est un isomorphisme de \(E\) sur \(F\) te permet d’affirmer que \(\text{dim}(E) = \text{dim}(F)\) (si tu ne le savais pas déjà) ;
– dans tous les cas, s’il existe une application \( \phi \) qui soit un isomorphisme de \(E\) sur \(F\), alors on dira que \(E\) et \(F\) sont isomorphes ;
– enfin, si \(E = F\) et que \( \phi \) est un isomorphisme, alors \( \phi \) est en fait un isomorphisme spécial que l’on appelle automorphisme ! Cela devient très intéressant, car toutes les propriétés des endomorphismes peuvent alors s’appliquer.
Si tu veux réviser les incontournables de l’algèbre linéaire aux concours, n’hésite pas à aller lire cet article : Cinq notions d’algèbre linéaire pour aborder sereinement son année de kharré.