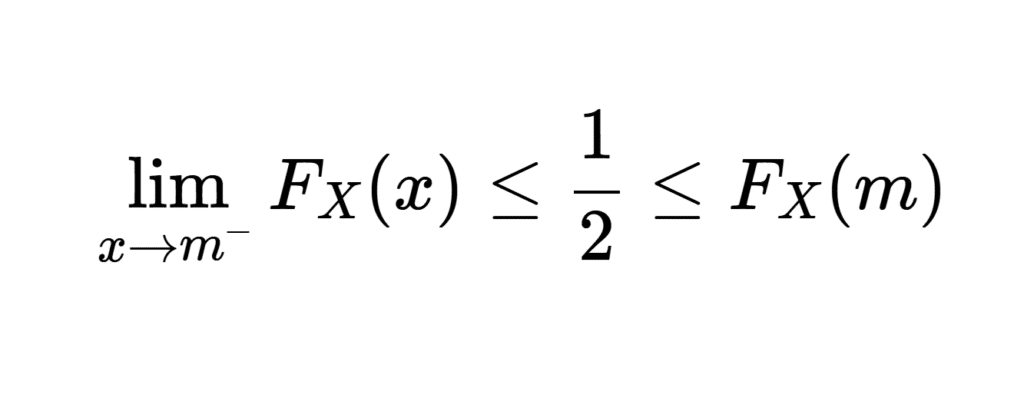Les notions hors programme sont particulièrement importantes pour quiconque prétend à une Parisienne. À ce titre, être familier avec les notions de mode et de médiane d’une variable aléatoire permettra de se préparer face à de telles épreuves. Ces notions sont aussi souvent utilisées pour les oraux de l’ESCP et de HEC.
Mode d’une variable aléatoire
Exemple avec une série statistique pour approcher la définition
Pour approcher une première fois la notion, prenons une série statistique que nous allons rassembler sous la forme d’un tableau. Pour simplifier tout ça, imaginons que l’on a une des notes obtenues à un devoir pour une classe et que l’on note le nombre de fois où la note i est obtenue (donc \(0 \leq i \leq 20\)).
On a donc, par exemple, le tableau suivant :
\[
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textbf{Note} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 \\
\hline
\textbf{Nombre d’élèves} & 2 & 3 & 1 & 3 & 2 & 1 & 2 & 3 & 1 & 3 & 2 & 1 & 5 & 2 & 1 & 2 & 3 & 1 & 2 & 3 & 1 \\
\hline
\end{array}
\]
Ici, le mode de la série statistique est la note qui est présente parmi le plus grand nombre d’élèves. C’est-à-dire 12 qui est répété 5 fois.
Autre tableau :
\[
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\textbf{Note} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 \\
\hline
\textbf{Nombre d’élèves} & 2 & 3 & 1 & 3 & 2 & 1 & 2 & 6 & 1 & 3 & 2 & 1 & 5 & 2 & 1 & 6 & 3 & 1 & 2 & 3 & 1 \\
\hline
\end{array}
\]
Ici, il existe deux modes de la série statistique (7 et 15) qui sont tous les deux répétés 6 fois. Remarque donc déjà que le mode n’est pas unique.
Définition
Pour définir le mode d’une variable aléatoire, nous allons devoir séparer le cas où l’on est face à une variable discrète de celui où l’on se trouve en présence d’une variable aléatoire à densité (même si, en fin de compte, les définitions se ressemblent beaucoup).
Premier cas : cas discret
Soit \( X \) une variable aléatoire discrète, telle que \( X(\Omega) = \{ x_k : k \in K \} \). On appelle mode de \( X \) toute valeur \( x_l \) telle que : \[ \forall k \in K, \, P(X = x_k) \leq P(X = x_l). \]
Second cas : cas à densité
Soit \( X \) une variable aléatoire absolument continue, de densité \( f \) continue sur \( \mathbb{R} \). On appelle mode de \( X \) tout réel \( x_0 \) où \( f \) atteint son maximum.
En fait, de manière générale, le mode d’une variable aléatoire discrète est donc sa valeur la plus probable et pour les variables à densité, cela signifie que le mode de la VAR est le point où la densité de probabilité est haute.
Propriétés du mode d’une variable aléatoire
Il n’y en a pas 36 à retenir, mais voici celles qui peuvent être utiles :
- Le mode est invariant par transformation affine de la variable aléatoire. Cela signifie que \(\forall(a,b) \in \mathbb{R^2}\) et \(X\) une variable aléatoire de mode \(m\), alors la variable aléatoire \(Y = aX+b\) est de mode \(am+b\).
- Pour faire la transition avec la partie sur la médiane, voici une petite propriété qui fait le lien entre mode et médiane. Pour une loi unimodale (qui possède un unique mode) d’écart-type \(\sigma\), la différence entre la moyenne et le mode est encadrée entre \(-\sqrt{3}\sigma\) et \(\sqrt{3}\sigma\).
Exemple
Posons \( X \hookrightarrow\mathcal{N}(\mu,\sigma^2)\). Dès lors, quel est le mode de \(X\) ?
En pensant graphiquement, on peut directement avoir une première idée de la réponse. On a dit que le mode de \(X\) était égal au maximum de sa densité de probabilité. Et une bonne connaissance du cours permet directement d’intuiter que le mode de \(X\) vaut \(\mu\). Mais maintenant, il faut le démontrer mathématiquement.
Pour trouver le maximum de la densité de probabilité d’une loi normale, posons \(f(x) = \frac{1}{\mu \sqrt{2\pi}}\exp(-\frac{1}{2}(\frac{(x-\mu)}{\sigma})^2)\). Mais on sait que \(g(x) = e^{-x^2}\) atteint un unique maximum sur \(\mathbb{R}\) pour \(x=0\) (tu peux passer par une petite étude de fonction pour redémontrer cela). Cela assure donc en regardant notre fonction \(f\) que son maximum est atteint pour une valeur de \(x\) vérifiant \(-\frac{1}{2}(\frac{(x-\mu)}{\sigma}) = 0\). On a donc immédiatement \(x=\mu\), ce qui conclut la démonstration.
Médiane d’une variable aléatoire
Définition
Soit \(X\) une variable aléatoire réelle, alors on appelle médiane de \(X\) le réel \(m\) vérifiant :
\[ \mathbb{P}(X \leq m) \geq \frac{1}{2} \quad \text{et} \quad \mathbb{P}(X \geq m) \geq \frac{1}{2} \]
C’est-à-dire, en termes de fonction de répartition : \[ \lim_{x \to m^-} F_X(x) \leq \frac{1}{2} \leq F_X(m) \]
Dans le cas d’une fonction de répartition continue, on déduit directement la proposition précédente que l’on cherche directement \(m\) tel que \[ F_X(m) = \frac{1}{2} \]
Exemples
Loi uniforme à densité
Considérons une variable aléatoire \( X \sim \mathcal{U}(a, b) \).
La densité de probabilité de \( X \sim \mathcal{U}(a, b) \) est donnée par :
\[f_X(x) =\begin{cases}\frac{1}{b – a} & \text{si } x \in [a, b] \\0 & \text{sinon}\end{cases}\]
Cette densité est constante sur l’intervalle \([a, b]\), ce qui signifie que chaque valeur de cet intervalle est également probable (cela permet déja d’avoir une idée de la médiane).
La fonction de répartition de \( X \sim \mathcal{U}(a, b) \) est donnée par :
\[F_X(x) =\begin{cases}0 & \text{si } x < a \\\frac{x – a}{b – a} & \text{si } x \in [a, b] \\1 & \text{si } x > b\end{cases}\]
Sur l’intervalle \([a, b]\), la fonction de répartition est \( F_X(x) = \frac{x – a}{b – a} \). En posant \( F_X(m) = \frac{1}{2} \), nous obtenons :
\[\frac{m – a}{b – a} = \frac{1}{2}\]
\[m – a = \frac{b – a}{2}\]
d’où :
\[m = a + \frac{b – a}{2}\]
Cela se simplifie en :
\[m = \frac{a + b}{2}\]
Ainsi, pour une loi uniforme sur un intervalle quelconque \([a, b]\), la médiane est simplement le point milieu de cet intervalle.
Loi normale centrée réduite
La fonction de répartition de \( X \sim \mathcal{N}(0, 1) \) est donnée par :
\[
F_X(x) = \mathbb{P}(X \leq x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}} \, dt
\]
Pour la loi normale centrée réduite \( \mathcal{N}(0,1) \), la densité est symétrique par rapport à l’origine (zéro), ce qui implique que :
\[\mathbb{P}(X \leq 0) = \mathbb{P}(X \geq 0) = \frac{1}{2}\]
Cette symétrie indique que \( x = 0 \) divise exactement la distribution en deux parties égales.
Puisque la médiane \( m \) est définie comme la valeur pour laquelle \( \mathbb{P}(X \leq m) = \frac{1}{2} \), et que nous avons démontré que \( \mathbb{P}(X \leq 0) = \frac{1}{2} \), il en résulte que :
\[m = 0\]
Ainsi, la médiane d’une loi normale centrée réduite est bien égale à zéro.
Conclusion
En définitive, la notion de mode et de médiane d’une variable aléatoire sont à connaître pour quiconque prétend aux Parisiennes. Ces notions tombent souvent, aux écrits comme aux oraux. Évidemment, ces notions peuvent toujours tomber dans des sujets du type EDHEC/Emlyon, mais sont plus rares. Il n’y a plus qu’à croiser les doigts pour que le sujet de cette année tombe sur ces notions !
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques.