L’étude des suites est un thème récurrent dans les sujets de concours, et s’il y a bien une question qui revient à chaque fois, c’est celle de l’étude de la convergence d’une suite donnée. Dans cet article, tu verras toutes les méthodes classiques pour montrer qu’une suite converge.
Définition de la convergence d’une suite
Avant de rentrer dans le vif du sujet, il est nécessaire de rappeler la définition d’une suite convergente, afin de mieux comprendre les points suivants.
Tout d’abord, on peut dire qu’une suite converge quand elle admet une limite finie en \(+ \infty\), c’est-à-dire qu’il existe \( \ell\in\mathbb{R}\) tel que \(\underset{n \rightarrow + \infty}{\lim}u_n = \ell\)
Mais si on veut être rigoureux, on peut définir la convergence d’une suite \((u_n)\) de cette manière : \((u_n)\) converge et admet \(\ell\) comme limite en \(+\infty\) (à noter qu’il y a unicité de la limite) si, et seulement si, \(\forall \varepsilon
>0,\ \exists n_{0}
>0,\ \forall n \ge
n_{0},|u_{n}-\ell|
< \varepsilon\)
Cette définition, qui peut sembler abrupte de prime abord, se comprend assez facilement à l’aide d’un schéma :
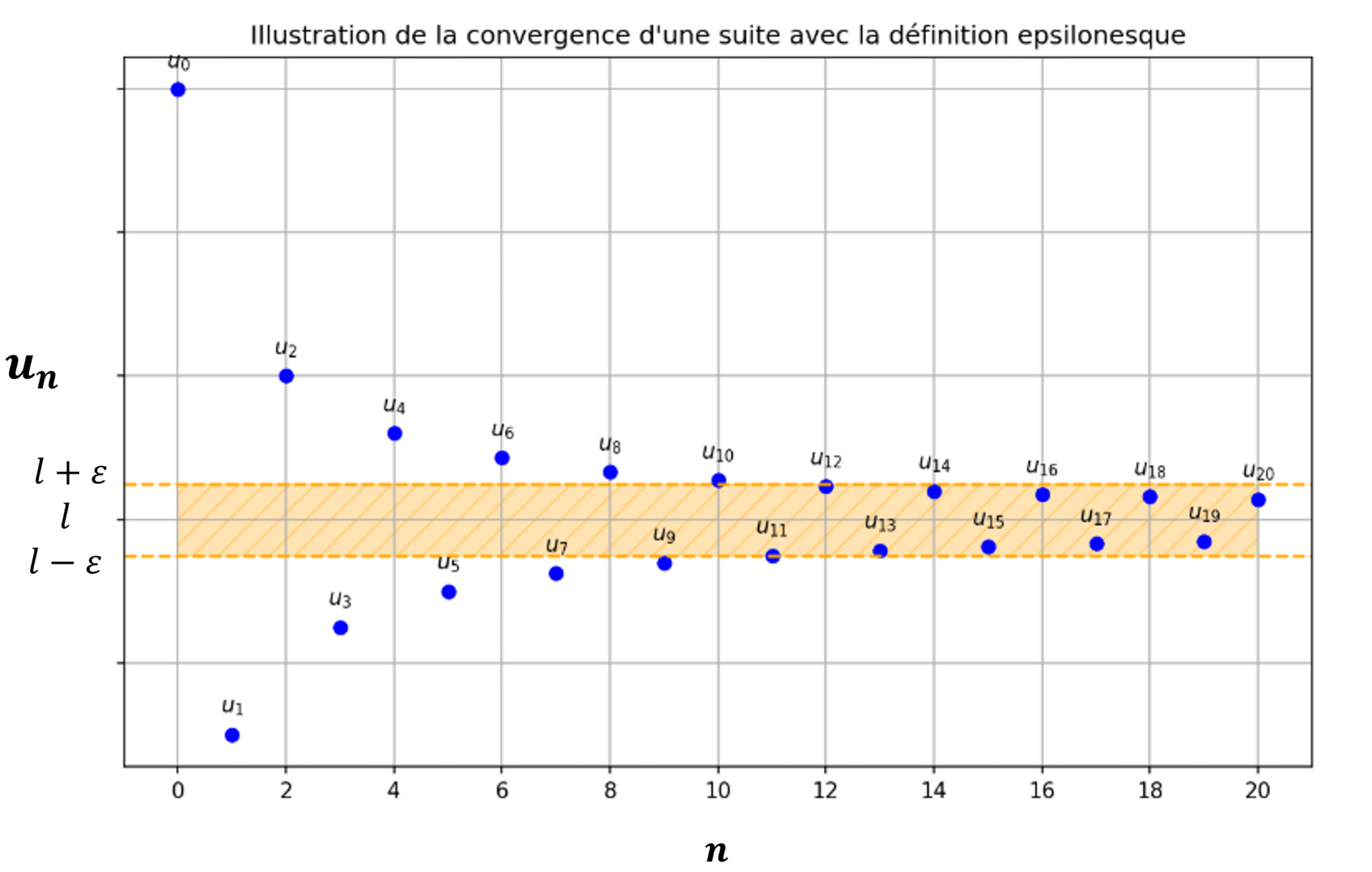
En l’occurrence, avec cette suite, pour ce \(\varepsilon\) donné, \(n_0\) correspond à 11 car, à partir du \(11^{ième}\) terme de la suite \(u_n\), tous les termes suivants de la suite sont compris dans la zone hachurée (à noter que le \(n_0\) de la définition varie en fonction du \(\varepsilon\) considéré ; si on avait pris un plus grand \(\varepsilon\), la zone hachurée aurait été plus grande, et donc \(n_0\) aurait été plus petit, et vice versa avec un plus petit \(\varepsilon\) ).
Convergence des suites classiques
Les suites qui suivent reviennent fréquemment et font partie du cours, il faut donc savoir quand elles convergent.
Les suites arithmétiques
Le cas des suites arithmétiques est trivial : elles convergent uniquement quand la raison \(r\) est nulle, puisqu’elles s’écrivent sous la forme \(u_n = nr + u_0\).
Les suites géométriques
De même, l’étude de la convergence des suites géométriques est simple : elles convergent uniquement quand la raison \(q\) est comprise entre \(]-1,1]\), puisqu’elles s’écrivent sous la forme \(u_n = u_0q^n.\)
Les suites arithmético-géométriques
Quand on se donne une suite arithmétique \((u_n)\) définie par la relation de récurrence suivante : \(u_{n+1}=au_n+b\), avec \((a,b)\in\mathbb{R^2}\), on distingue plusieurs cas de convergence :
Si \(a = 1\), on se ramène au cas des suites arithmétiques vu précédemment.
Si \(a\ne 1 \), après étude de la suite, en notant \(c= \frac{b}{1-a}\), on a \(u_n=a^n(u_o – c) +c \). Par conséquent, on remarque qu’on se ramène au cas des suites géométriques, avec \(a\) à la place de \(q\), vu précédemment.
Le théorème de la limite monotone
Ce théorème, très puissant pour montrer la convergence d’une suite, est un incontournable des concours.
Il y a deux variantes du théorème :
- Si \((u_n)\) est décroissante et minorée, alors \((u_n)\) converge.
- Si \((u_n)\) est croissante et majorée, alors \((u_n)\) converge.
Dans la pratique, il est assez simple d’utiliser ce théorème. En effet, calculer \(u_{n+1}-u_n\) permet en général de déterminer la monotonie d’une suite et il suffit, en particulier dans le cas où on a une suite décroissante, de trouver un minorant, généralement 0.
Astuce : pour montrer la monotonie d’une suite, on peut également considérer \(\frac{u_{n+1}}{u_n}\) : si \(\frac{u_{n+1}}{u_n}\le 1\), alors la suite est décroissante et si \(\frac{u_{n+1}}{u_n}\ge 1\), alors la suite est croissante. À noter qu’il faut bien sûr que la suite \((u_n)\) ne s’annule pas pour pouvoir utiliser ce quotient.
Le théorème des gendarmes
De même que pour le théorème précédent, ce dernier est omniprésent dans les sujets de concours. Il permet de montrer la convergence d’une suite \((u_n)\), en l’encadrant avec deux suites convergentes \((v_n)\) et \((w_n)\).
En effet, si à partir d’un certain rang \(n\), on a \(v_n\le u_n\le w_n\), avec \((v_n)\) et \((w_n)\) qui convergent vers la même limite \(\ell\), alors \((u_n)\) converge vers \(\ell\) également.
Attention à ne pas oublier de mentionner ce théorème quand tu l’utilises !
Les suites extraites de rang pair et impair
La propriété suivante est très efficace pour montrer la converge d’une suite qui change constamment de signe (par exemple, lorsqu’il y a un \((-1)^n\) dans la formule explicite de la suite considérée \((u_n)\)).
Si \(\underset{n \rightarrow + \infty}{\lim}u_{2n} = \ell = \underset{n \rightarrow + \infty}{\lim}u_{2n+1} = \ell\), alors \((u_n)\) converge et \(\underset{n \rightarrow + \infty}{\lim}u_n = \ell.\)
Cette méthode est généralement suggérée dans les exercices lorsque tu dois y recourir.
Les équivalents
Si on se donne deux suites \((u_n)\) et \((v_n)\), avec \(\underset{n \rightarrow + \infty}{\lim}v_n= \ell\) et \(u_n\underset{+\infty}{\sim}v_n\), alors \((u_n)\) converge et \(\underset{n \rightarrow + \infty}{\lim}u_n = \ell.\)
Dans les faits, cette propriété est assez difficile à utiliser, car quand on est capable de donner un équivalent simple d’une suite, ça signifie qu’on est généralement capable de calculer sa limite et donc de déterminer sa convergence ou non. Toutefois, il est toujours bon de se rappeler qu’il existe cette méthode.
Les suites adjacentes
Tout d’abord, il faut rappeler la définition de ce que sont les suites adjacentes : on dit que deux suites \((u_n)\) et \((v_n)\) sont adjacentes quand l’une est croissante, l’autre est décroissante et \(\underset{n \rightarrow + \infty}{\lim}(u_n-v_n) = 0.\)
Dans ce cas, \((u_n)\) et \((v_n)\) sont convergentes et tendent vers la même limite finie \(\ell.\)
Lien entre les séries télescopiques et la convergence d’une suite
La propriété qui suit revient assez fréquemment dans les sujets de concours (cf. oraux ESCP 2023) et est très simple à démontrer et à comprendre :
\(\displaystyle \sum_{k=0}^{+\infty}(u_{k+1}-u_k)\)converge \(\Leftrightarrow\) \((u_n)\) converge.
En effet, soit \(N\in\mathbb{N^*}\), on a :
\(\begin{align}\displaystyle \sum_{k=0}^{N}(u_{k+1}-u_k) &=\displaystyle \sum_{k=0}^{N}u_{k+1} – \displaystyle \sum_{k=0}^{N}u_{k} \text { linéarité de la somme}\\ &= \displaystyle \sum_{k=1}^{N+1}u_{k} – \displaystyle \sum_{k=0}^{N}u_{k} \text{ changement d’indice dans la première somme}\\ &= u_{N+1} – u_0\end{align}\)
On a donc \(\underset{N \rightarrow + \infty}{\lim} \displaystyle \sum_{k=0}^{N}(u_{k+1}-u_k)\ = \underset{N \rightarrow + \infty}{\lim}(u_{N+1}-u_0).\) D’où la propriété précédente.
Piège à éviter
Un piège très classique consiste à considérer que si une suite \((u_n)\) est bornée, alors elle converge. Or, l’implication ne fonctionne que dans l’autre sens !
En effet, si on considère la suite \(u_n=1+sin(n)\), on remarque qu’elle est minorée par 0 et majorée par 2, donc elle est bornée. Toutefois, on remarque qu’elle ne converge pas, à cause du sinus qui varie entre – 1 et 1.
Conclusion
Ainsi, tu as désormais tous les outils à disposition pour montrer qu’une suite converge ! Tu peux aller t’exercer en consultant ces annales :
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !